25.03 Четырёхугольники
Ошибка.
Попробуйте повторить позже
Найдите площадь трапеции, диагонали которой равны 17 и 15, а средняя линия равна 4.
Пусть не умаляю общности и
. Проведем через точку
прямую, параллельную диагонали
.
Пусть она пересекает прямую
в точке
. Тогда
— параллелограмм, так как
и
,
значит,
и
.
Вспомним, что длина средней линии равна полусумме длин оснований, значит,
![]()
Рассмотрим треугольник . В нем
,
и
. Заметим, что
,
значит, по теореме, обратной теореме Пифагора,
— прямоугольный. Следовательно,
— высота трапеции
. Тогда
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Основания трапеции относятся как Через точку пересечения диагоналей
проведена прямая, параллельная основаниям. В каком отношении эта прямая
делит площадь трапеции?
Пусть и
— основания трапеции
причем
по
условию. Пусть
— точка пересечения диагоналей трапеции, а
— прямая,
параллельная основаниям, которая проходит через точку
(точка
лежит на
точка
— на

Рассмотрим треугольники и
Они подобны по двум углам:
как вертикальные,
как накрест лежащие,
образованыые параллельными прямыми
и
и секущей
Тогда
Пусть и
— высоты треугольников
и
соответственно. Тогда
треугольники
и
подобны по двум углам:
и
Следовательно,
Рассмотрим треугольники и
Они подобны по двум углам:
— общий,
как соответственные, образованные
параллельными прямыми
и
и секущей
Тогда
Аналогично рассмотрим треугольники и
докажем, что они
подобны, и выведем
Запишем формулу площади трапеции
Запишем формулу площади трапеции
Тогда
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике диагонали пересекаются в точке
Точка
принадлежит отрезку
Известно, что
Найдите
если площадь треугольника
в три раза меньше площади
четырехугольника
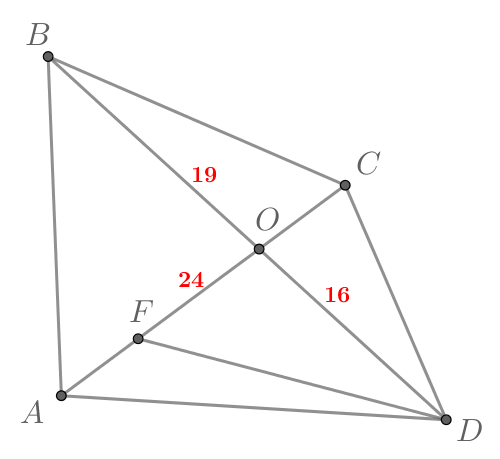
Площади треугольников, имеющих одинаковую высоту, относятся как основания, к
которым проведена эта высота. Так как у треугольников и
общая высота, проведенная к основаниям
и
соответственно,
то
Так как у треугольников и
общая высота, проведенная к
основаниям
и
соответственно, то
Тогда
По условию
Тогда
С другой стороны,
так как треугольники и
имеют общую высоту, проведенную к
основаниям
и
соответственно.
Значит,
Найдем
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В трапеции боковая сторона
перпендикулярна основанию
Окружность проходит через точки
и
и касается прямой
в точке
Найдите расстояние от точки
до прямой
если
![]()
По условию сторона перпендикулярна основанию
поэтому
Так как
то по свойству параллельных прямых
поэтому
Расстояние от точки до прямой
– длина перпендикуляра,
проведенного из точки
к прямой
Опустим из точки
перпендикуляр
на сторону
Нужно найти длину
Угол между касательной и хордой равен половине угловой величины дуги,
заключенной между ними, тогда так как оба этих угла равны
половине дуги
Аналогично
Рассмотрим треугольники и
В них
Тогда по двум углам. Запишем отношение подобия:
Аналогично рассмотрим треугольники и
В них
Тогда по двум углам. Запишем отношение подобия:
Из первого отношения подобия получаем:
Из второго отношения подобия получаем:
Тогда:
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Найдите площадь трапеции, диагонали которой равны 10 и 8 , а средняя линия равна 3.
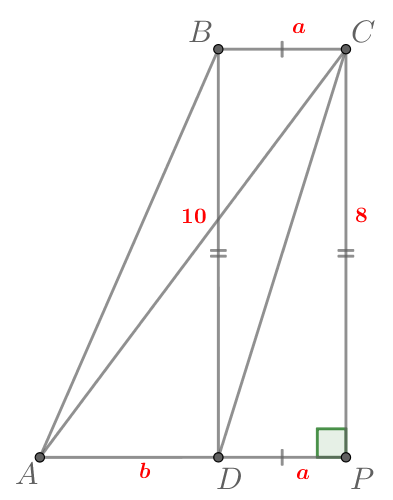
— трапеция с основаниями
и
По условию
Пусть
По свойству средней линии длина средней линии равна полусумме оснований:
Проведем через точку прямую
Рассмотрим четырехугольник
Тогда — параллелограмм по определению.
По свойству параллелограмма
Рассмотрим треугольник
- 1.
- 2.
- 3.
По теореме, обратной теореме Пифагора, треугольник прямоугольный,
Значит,
— высота трапеции
Так как площаль трапеции равна произведению полусуммы ее оснований на высоту, то
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В равнобедренную трапецию, периметр которой равен 160, а площадь равна 1280, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Пусть — трапеция с основаниями
и
Так как трапеция
равнобедренная, то
Пусть
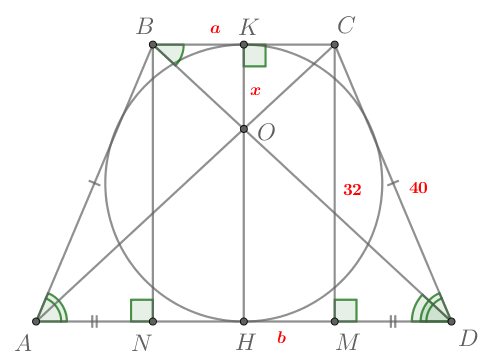
Трапеция описанная, значит, по свойству описанного четырехугольника
По условию периметр трапеции равен 160, то есть
Тогда
Пусть
Тогда
Опустим высоты и
Так как площадь трапеции равна произведению
полусумме оснований на высоту, то
Если две прямые перпендикулярны третьей прямой, то они параллельны. Так
как и
то
Рассмотрим четырехугольник В нем
и
как
основания трапеции, следовательно,
Тогда — параллелограмм и
по свойству параллелограмма.
Рассмотрим треугольники и
В них
как углы при основании равнобедренной трапеции и
Тогда треугольники и
равны по острому углу и гипотенузе.
как соответственные элементы.
В треугольнике по теореме Пифагора
Значит, Так как
то
Найдем
Проведем высоту проходящую через точку
Так
как
— высота трапеции, то
Рассмотрим треугольники и
В них
как накрест лежащие углы при параллельных прямых
и
а
как вертикальные.
Тогда по двум углам. Значит, отношение их соответственных
высот равно коэффициенту подобию, то есть
Пусть Тогда
Так как расстояние от точки до прямой — это длина перпендикуляра,
опущенного на эту прямую из точки, то расстояние от точки пересечения
диагоналей трапеции до ее меньшего основания — длина то есть
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Боковые стороны и
трапеции
равны соответственно 40 и 41, а
основание
равно 16. Биссектриса угла
проходит через середину
стороны
Найдите площадь трапеции.
Обозначим середину за точку
Тогда
Пусть
пересекает
в точке
Так как
то
как накрест
лежащие при параллельных прямых. Так как
— биссектриса
то

Значит, треугольник — равнобедренный. Тогда
Рассмотрим треугольники и
как накрест
лежащие при параллельных прямых,
как вертикальные,
Тогда треугольники
и
равны по двум углам и
стороне между ними.
как соответственные элементы равных
треугольников.
Проведём прямую параллельную прямой
Так как
то
— параллелограмм. Значит, по свойству параллелограмма
Рассмотрим треугольник
По теореме, обратной теореме Пифагора, треугольник — прямоугольный,
Значит, — высота трапеции
Найдём её площадь:
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В равнобедренной трапеции боковые стороны равны меньшему основанию
К диагоналям трапеции провели перпендикуляры
и
Найдите
площадь четырёхугольника
если площадь трапеции
равна
36.
Так как по условию, то треугольники
и
—
равнобедренные. По свойству равнобедренного треугольника
— высота и
медиана треугольника
то есть
— высота и медиана
треугольника
то есть
Так как диагонали равнобедренной
трапеции равны, то
Пусть Пусть точка
— середина
точка
—
середина
Тогда в треугольнике
— средняя линия, в
треугольнике
— средняя линия, в треугольнике
—
средняя линия. По свойству средней линии
Так как то
Так как две прямые, параллельные третьей
прямой, параллельны, то точки
лежат на одной прямой, точки
лежат на одной прямой. Значит, точки
лежат на средней
линии трапеции
По свойству средней линии
Значит,
Найдём
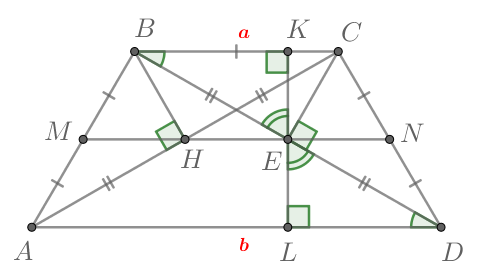
Проведём через точку высоту
трапеции
Тогда
Рассмотрим треугольники и
как накрест
лежащие при параллельных прямых,
как вертикальные,
Тогда треугольники
и
равны по двум углам и стороне
между ними. Значит,
как соответственные элементы равных
треугольников.
Найдём площадь трапеции
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В трапеции проведен отрезок, параллельный основаниям и делящий ее на две
трапеции одинаковой площади. Найдите длину этого отрезка, если основания
трапеции равны см и
см.
— отрезок, параллельный основаниям
и
и делящий
на две
трапеции одинаковой площади.
Пусть Так как соответственные углы при параллельных
прямых равны, то

Рассмотрим треугольники и
— общий,
Тогда
по двум углам. Площади подобных треугольников
относятся как квадрат коэффициента подобия, поэтому
Пусть Тогда
По условию
поэтому
Тогда
Рассмотрим треугольники и
— общий,
Тогда
по двум углам.
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
параллелограмма
пересекаются в точке
Найдите площадь параллелограмма, если
а расстояние от точки
до
стороны
равно 1.

Проведём По условию расстояние от точки
до стороны
равно
1, то есть
Проведём высоту параллелограмма
через точку
Рассмотрим прямоугольные треугольники и
так как
— биссектриса
— общая. Тогда треугольники
и
равны по острому углу и гипотенузе,
как соответственные
элементы равных треугольников.
Рассмотрим прямоугольные треугольники и
так как
— биссектриса
— общая. Тогда треугольники
и
равны по острому углу и гипотенузе,
как соответственные
элементы равных треугольников.
Тогда
Площадь параллелограмма равна произведению основания на высоту, проведённую к ней, поэтому
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |



