.03 Неравномерное движение
Ошибка.
Попробуйте повторить позже
Тело движется вдоль оси из точки с координатой
. Проекция скорости тела на ось
зависит от его
координаты
по закону
, где
известная постоянная. Через какое время тело окажется в точке с
координатой
?
Источники:
Движение тела не является ни равномерным, ни равноускоренным. Поэтому готовых соотношений для нахождения
времени его попадания в те или иные точки нет. Поэтому будем вычислять время, исходя из определения скорости.
Для этого мысленно разобьем траекторию на элементы ,
,
,
– настолько малые, что
скорость на каждом из них можно считать постоянной. Тогда время прохождения
-го элемента
равно
где – скорость тела в какой-то точке внутри
-го элемента. Поэтому время прохождения участка траектории,
лежащего от координаты
до координаты
определяется суммой времен прохождения всех малых элементов, на
которые можно разделить этот участок траектории
Сумму в скобках приходится вычислять при вычислении работы силы упругости. И вычисляется она графически. Для
ее вычисления нужно построить график зависимости . Тогда сумма (*) равна площади под графиком
между
вертикальными прямыми
и
(показаны на рисунке пунктиром).
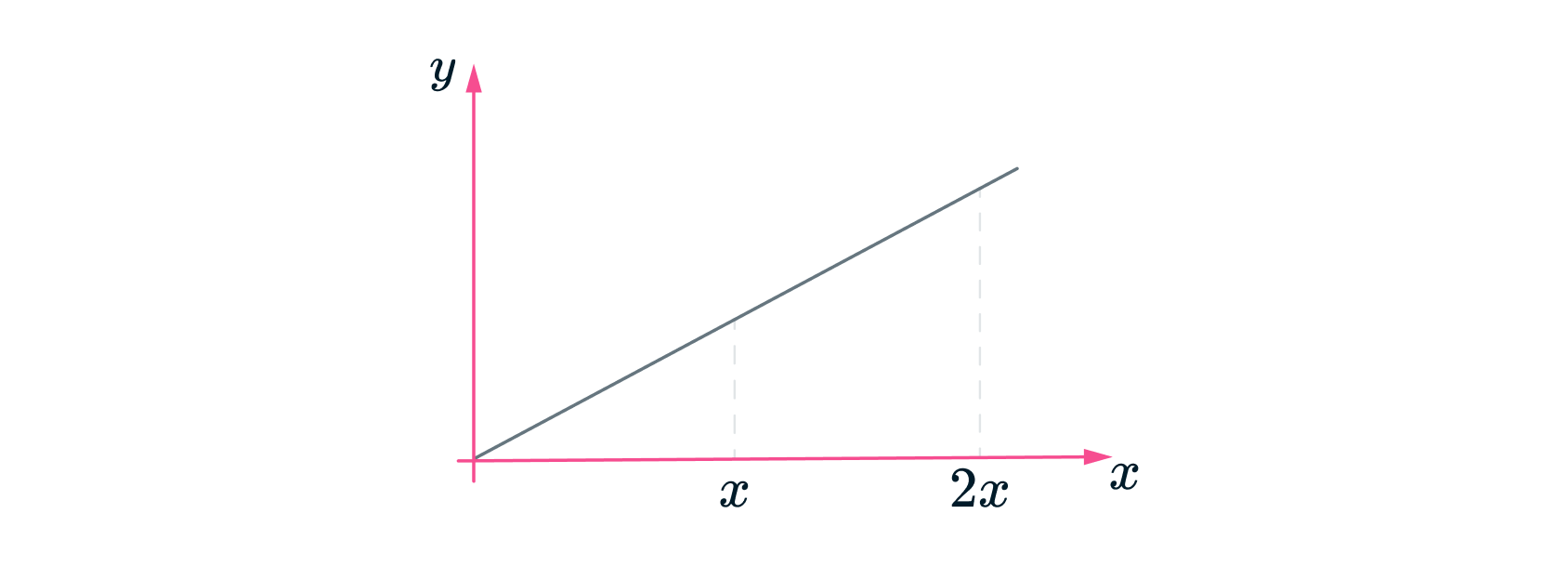
Эта фигура представляет собой трапецию с высотой и основаниями
и
. Находя площадь этой трапеции,
получим
(Официальное решение Росатом)
| Критерии оценивания выполнения задачи | Баллы |
| Правильная идея и обоснование решения – вычисление площади под графиком функции | 2 |
| Правильно построен график этой функции | 2 |
| Правильно выбраны границы суммирования | 3 |
| Правильный ответ | 3 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




