.04 Относительность движения
Ошибка.
Попробуйте повторить позже
Из точек и
, находящихся на одной горизонтальной прямой, одновременно бросили два камня с одинаковыми по модулю
скоростями
. Один из них полетел по навесной траектории, а другой – по настильной, и каждый упал в точку старта
другого камня. Известно, что угол бросания
камня из точки
составляет
(см. рисунок). Через какое время после бросания
расстояние между камнями станет минимальным? Чему равно это расстояние? Укажите на рисунке положения камней в этот
момент.
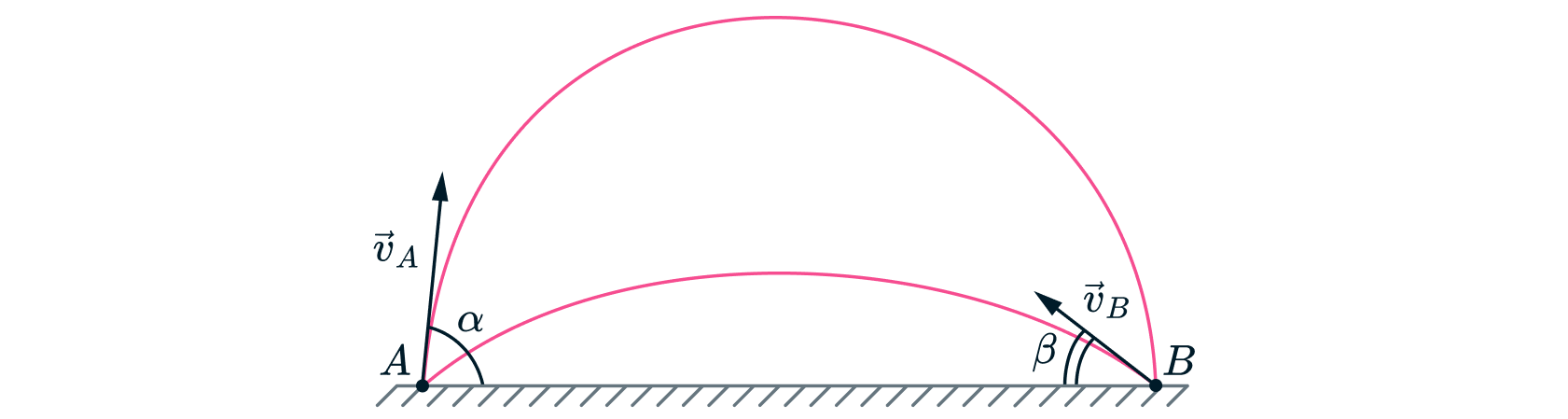
Пусть – угол броска второго камня. Из условия видно, что дальности полетов камней равны. Запишем формулу дальности полета
для обоих камней и приравняем:
Отсюда:
Это возможно в двух случаях: либо , что в нашей ситуации неверно, либо
, что в нашем случае и
выполняется. Тогда:
Перейдем в систему отсчета второго камня и по правилу сложения скоростей найдем скорость первого камня относительно второго:
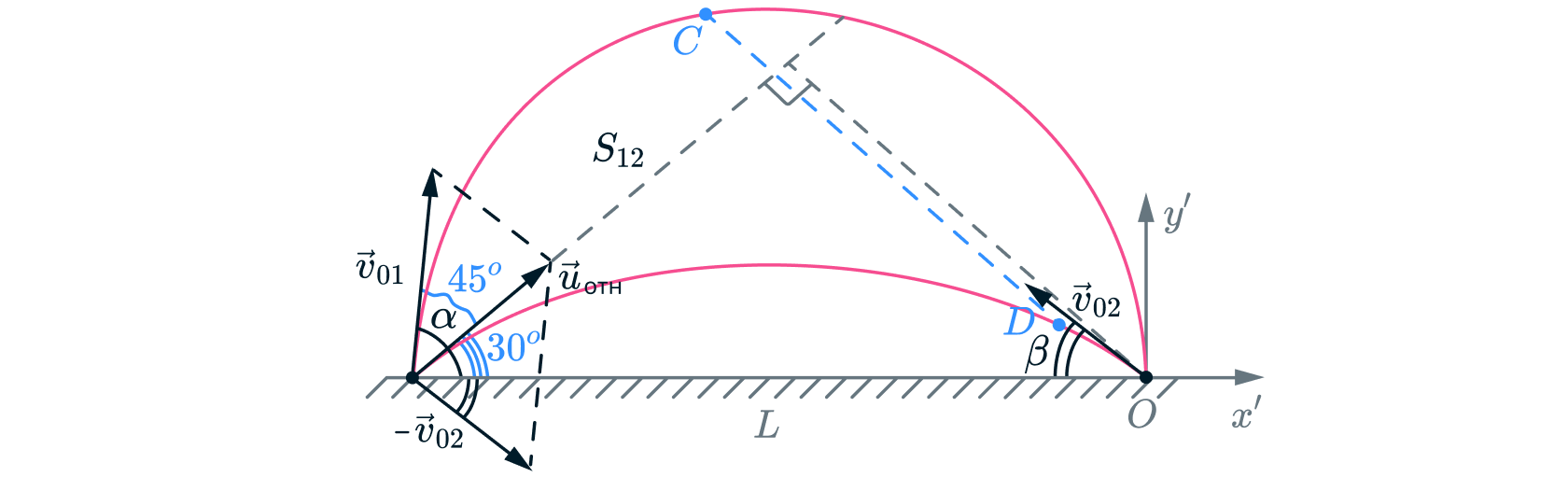
Поскольку модули скоростей камней равны, а сумма углов их бросков равна , полученный треугольник скоростей
прямоугольный и равнобедренный. Тогда угол под которым направлена скорость первого камня относительно второго к горизонтали
равен
. Модуль относительной скорости же:
Запишем правило сложения ускорений для двух камней и найдем ускорение первого камня относительно второго:
Получается, что относительного второго камня первый движется равномерно и прямолинейно. Тогда минимальное расстояние между камнями есть перпендикуляр из точки нахождения второго камня на прямую, вдоль которой движется первый камень относительно второго. Найдем дальность полета камней:
Из полученного прямоугольного треугольника минимальное расстояние между камнями:
Из того же треугольника расстояние, которое прошел первый камень относительно второго до положения, когда расстояние между ними минимально:
Тогда время движения первого камня относительно второго до этого положения:
Чтобы найти в каких положениях будут камни в этот момент в лабораторной системе отсчета перенесем параллельно отрезок
вдоль одной из траекторий до пересечения второго конца с другой траекторией.
Важное замечание: движение первого камня относительно второго будет оставаться равномерным и прямолинейным до тех пор, пока
оба камня находятся в полете. Как только один из камней упадет на землю, на него начнут действовать другие силы
и правило сложения ускорений в таком виде будет нарушаться. Значит чтобы наше решение оставалось верным
нужно удостовериться, что полученное время меньше минимального из времен полетов камней. По формуле времени
полета оно пропорционально синусу угла броска, значит меньшее время полета будет у второго камня и равно оно
будет:
Полученное нами время меньше минимального времени полета, значит все наши рассуждения остаются верными.
| Критерии оценивания выполнения задачи | Баллы |
| Записано равенство дальностей полетов | 1 |
| Получено отношение углов | 1 |
| Рассмотрен треугольник скоростей и найдена относительная скорость | 1 |
| Записано правило сложения ускорений | 1 |
| Описано и найдено минимальное расстояние между камнями | 2 |
| Найдено искомое время | 2 |
| Указаны искомые положения камней | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




