.04 Относительность движения
Ошибка.
Попробуйте повторить позже
Жесткий стержень AB движется под действием некоторых сил так, что его концы А и В скользят по вертикальной стене и
горизонтальному полу соответственно (см. рисунок). В некоторый момент времени, когда стержень составляет угол
градусов с полом, ускорение точки C , лежащей на расстоянии четверти длины стержня от точки А, направлено вдоль
стержня вниз (см. рисунок) и равно по величине
. Найти ускорения концов стержня в этот момент.
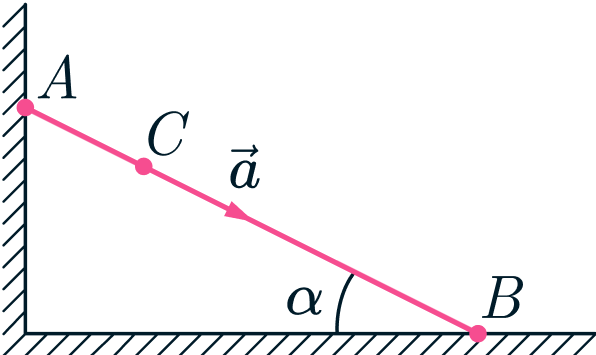
(Росатом 2025, 10)
Источники:
Решим сначала вспомогательную задачу. Пусть жесткий стержень длиной движется произвольным образом и скорости
его концов
и
в некоторый момент времени известны. Найдем в этот момент скорость точки С стержня, лежащей
на расстоянии
от конца 1 .
Перейдем в систему отсчета, связанную с концом В нашего стержня. В ней этот конец стержня покоится, а скорость
конца А определяется законом сложения скоростей
При этом вектор направлен перпендикулярно стержню, поскольку движение стержня в этой системе
отсчета - вращение вокруг конца В. Значит, и скорости всех остальных точек стержня в этой системе отсчета
перпендикулярны стержню, а их величина пропорциональна расстоянию от каждой точки до второго конца. Поэтому
величина скорости точки С в этой системе отсчета составляет
от скорости
и сонаправлена с ней.
Поэтому
Чтобы найти скорость точки С в системе отсчета, связанной с землей, снова воспользуемся законом сложения
скоростей. Имеем
А поскольку такая связь справедлива в любой момент времени, такой же является и связь ускорений этих точек
Вернемся теперь к нашей задаче. С одной стороны, ускорение точки С направлено вдоль стержня, с другой, - связано
предыдущей формулой с ускорениями и
, которые направлены вдоль вертикальной стены и горизонтального пола
соответственно. Поэтому для величин этих ускорений имеем
Решая эту систему уравнений, получим
Обратим внимание на то, что проекции векторов ускорений концов стержня на сам стержень (в отличие от скоростей) не равны друг другу.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




