.04 Относительность движения

Поместим начало координат в центр Солнца и введём вектор , направленный вдоль отрезка, соединяющего центры Солнца и планеты. Введём также вектор , жёстко связанный с планетой и направленный от её центра к произвольной точке на экваторе. Этот вектор участвует в осевом вращении вместе с планетой и определяет положение наблюдателя на экваторе. В дальнейшем нас будут интересовать только направления введённых векторов. Поэтому будем считать их единичными.

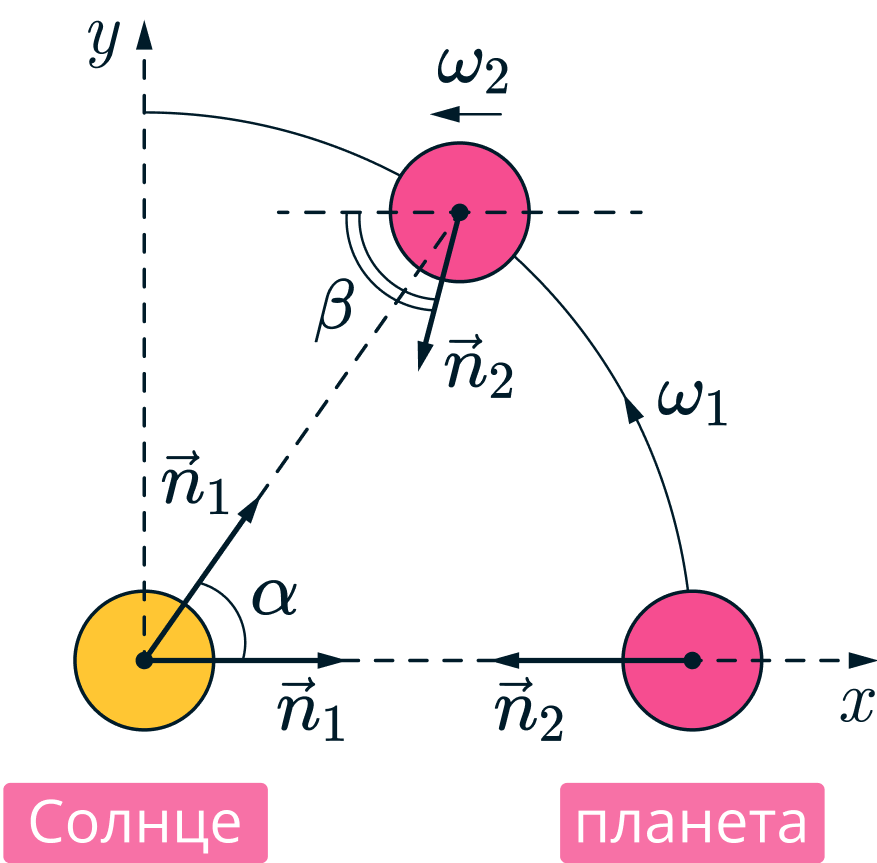
Предположим, что в некоторый момент для наблюдателя наступил полдень, то есть Солнце оказалось в зените. В этом случае векторы и направлены противоположно друг другу. Примем этот момент за начало отсчёта времени, ось системы координат направим вдоль вектора , ось — в сторону орбитального движения планеты. За время векторы и повернутся относительно своих начальных положений на углы и :

и — угловые скорости орбитального и осевого вращений:

Координаты векторов равны:

Следующий полдень наступит в момент, когда векторы и снова окажутся направленными противоположно. Это условие удобно записать через скалярное произведение:

Переходя к координатам, получаем:

Здесь — целое число. Продолжительность солнечных суток является наименьшим положительным значением . При оно получается при в зависимости от знака разности . Обе возможности можно учесть, взяв модуль разности. Окончательно получаем:

Количества оборотов и определяются значениями углов поворота и за время :