.04 Относительность движения
Ошибка.
Попробуйте повторить позже
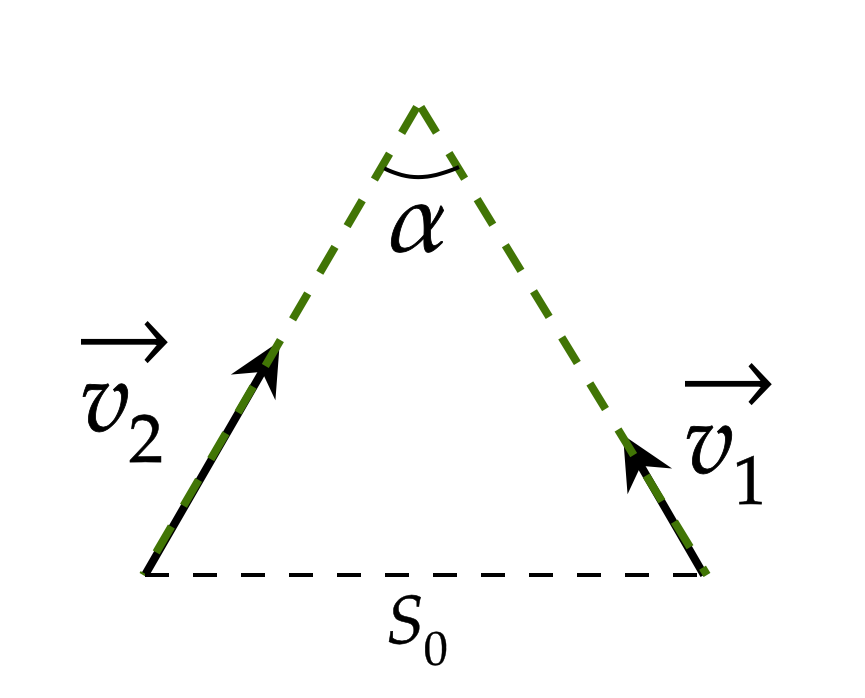
Два корабля двигаются в море со скоростями и
, при этом скорости
направлены таким образом, что траектории кораблей пересекаются под углом
(см.
рисунок). Корабли расположены таким образом, что расстояние между кораблями равно
, расстояния между кораблями и точкой пересечения траекторий равны. Через
какое время расстояние между кораблями станет минимальным? Найдите это расстояние.
I способ
Перейдем в систему отсчета, связанную с первым кораблем.
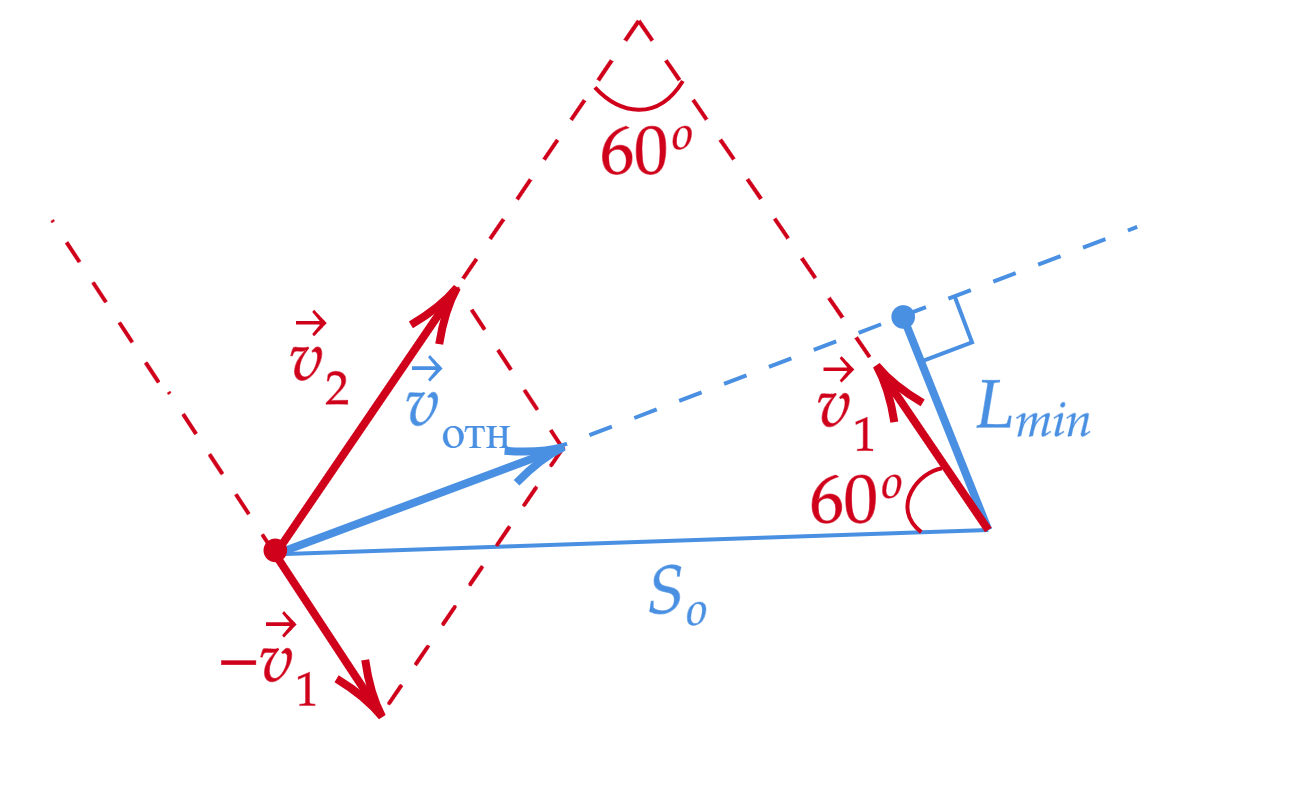
Тогда относительная скорость равна
Чтобы найти угол рассмотрим треугольник со сторонами
. Угол между сторонами
и
равен
По теореме косинусов
По теореме синусов найдем
А угол равен
, значит, траектория относительного движения является
биссектрисой, а в равностороннем треугольнике она является еще и медианой, следовательно,
. Следовательно:
II способ
До момента пересечения траекторий корабли будут сближаться, после пересечения траекторий корабли
будут удаляться. Значит минимальное расстояние в точке пересечения траекторий. Так как скорость
второго в 2 раза больше, чем скорость первого, то он придет в точку пересечения в 2 раза быстрее, а
расстояние между кораблями будет равно половине траектории. Заметим, что треугольник
равносторонний (равнобедренный, с углом при пересечении одинаковых ребер 60 градусов),
значит длина траектории равна . Так как расстояние между кораблями равно
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




