.04 Относительность движения
Ошибка.
Попробуйте повторить позже
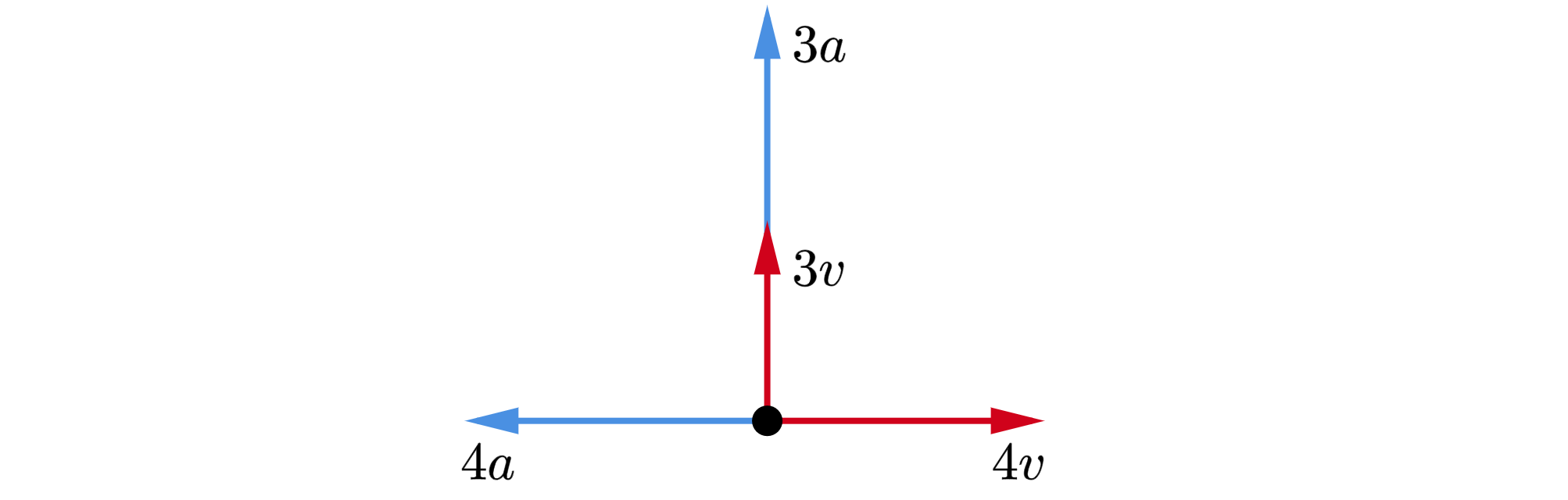
Две частицы начали движение из одной точки во взаимно перпендикулярных направлениях (рис.). Первая — с начальной
скоростью и постоянным ускорением
, сонаправленным с начальной скоростью, другая — со скоростью
и
постоянным ускорением
, направленным противоположно начальной скорости. Численно
,
.
Каким будет расстояние
между частицами в момент, когда их относительная скорость по модулю опять станет равна
начальной относительной скорости? Чему будет равна минимальная относительная скорость
частиц?
(Всеросс., 2013, финал, 9 )
Источники:
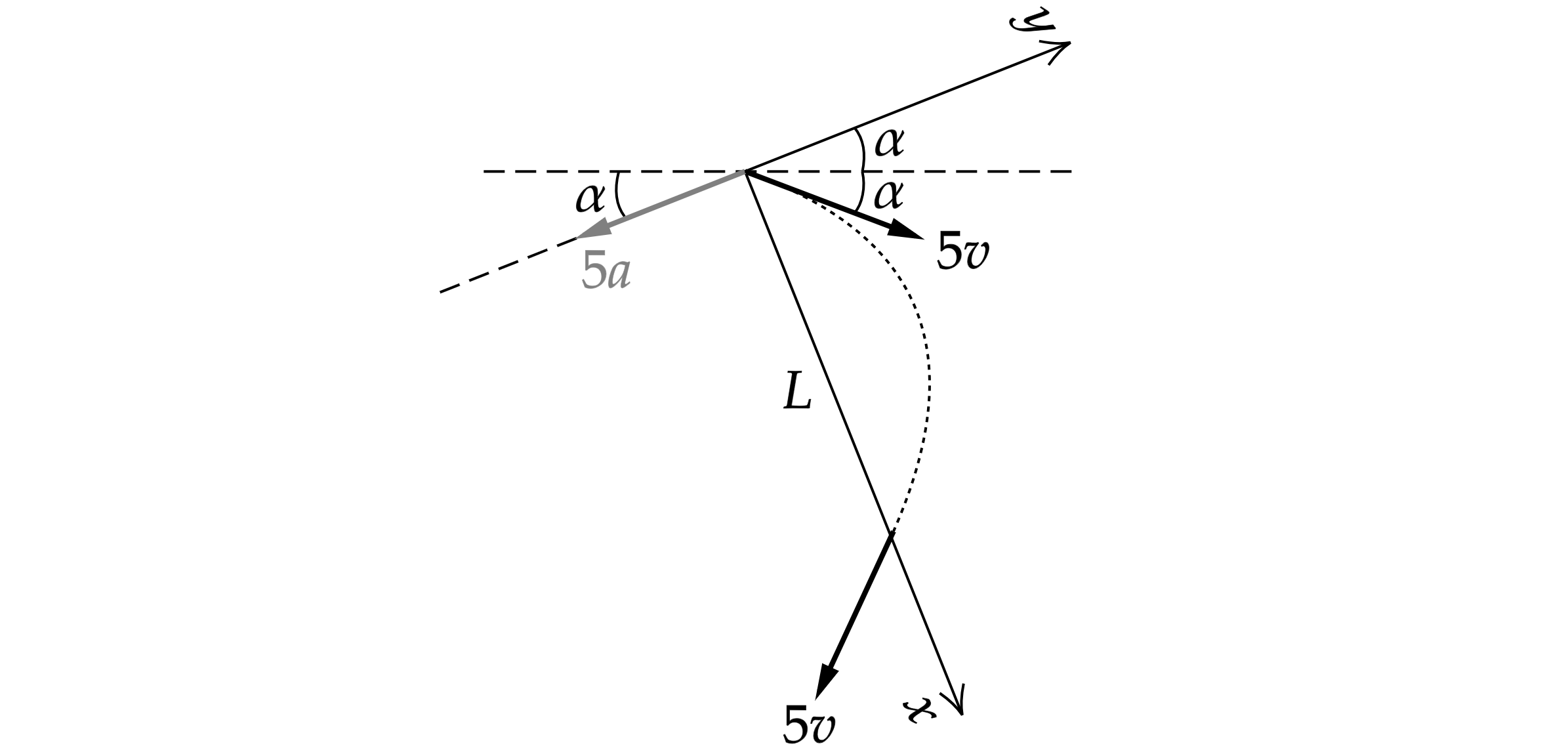
Перейдём в систему отсчета, связанную с первой частицей, используя правила сложения скоростей и ускорений:
Рассмотрим движение второй частицы как полет вдоль некоторой оси , с начальной скоростью
, направленной
под углом
к перпендикулярной оси
, вдоль которой действует ускорение
. Угол
найдем из прямоугольного
треугольника скоростей или ускорений:
По формуле для дальности полета тела, брошенного под углом к горизонту:
По аналогии с обычным броском относительная скорость будет минимальна в верхней точке траектории. Отсюда:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




