.04 Относительность движения
Ошибка.
Попробуйте повторить позже
Ракета удаляется от горизонтальной поверхности Земли со скоростью , направленной строго вертикально. Параллельно
поверхности точно на запад летит самолёт со скоростью
.
1) С какой наименьшей по модулю скоростью и в каком направлении должен лететь (относительно Земли)
квадрокоптер для того, чтобы относительно него ракета и самолёт имели противоположные по направлению
скорости?
2) Под каким углом к горизонту (относительно Земли) должна быть направлена скорость квадрокоптера для того, чтобы
ракета и самолёт имели в системе отсчёта квадрокоптера противоположные по направлению и равные по модулю
скорости? Чему равен модуль скорости квадрокоптера в этом случае?
(МОШ, 2017, 9)
Источники:
Найдём относительные скорости:
Вычтем из верхнего нижнее
Как можно заметить, относительная скорость ракеты относительно самолёта, лежит на той же прямой, что и относительные скорости относительно квадрокоптера.
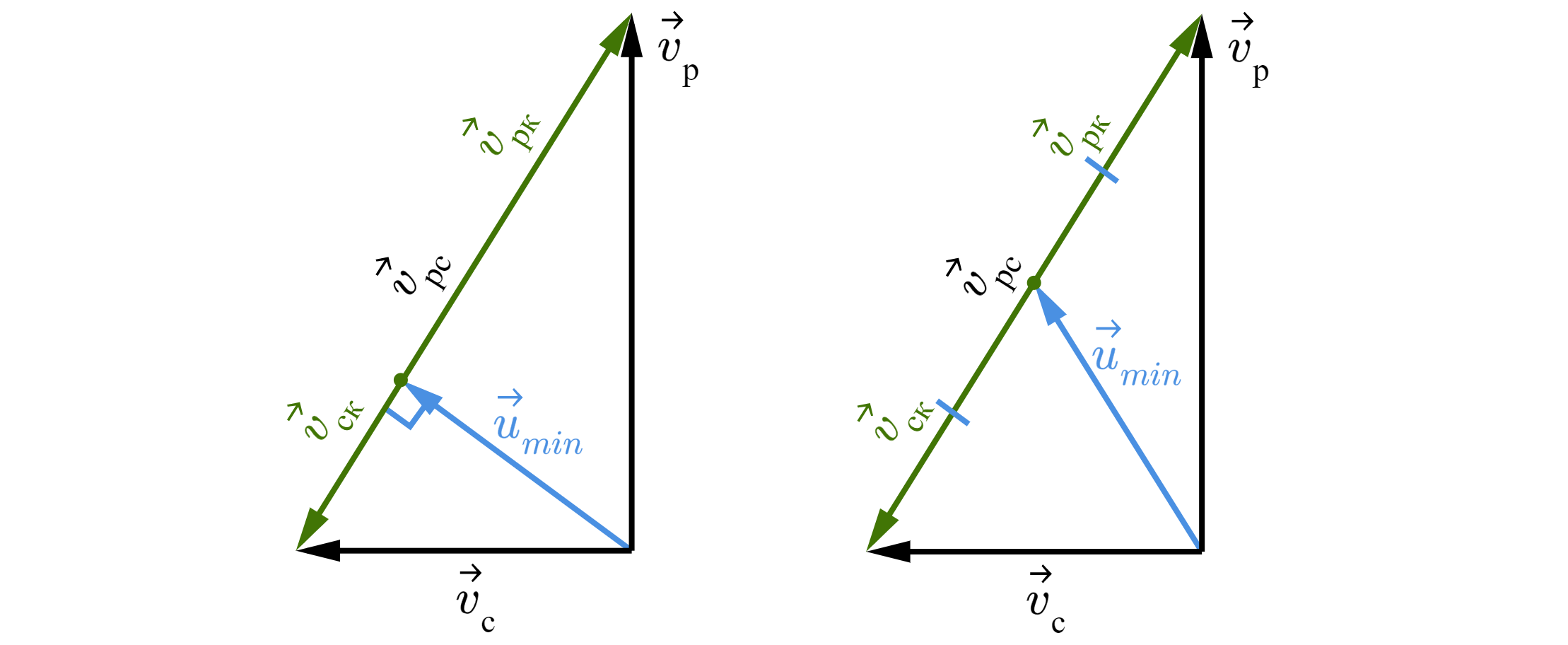
Тогда минимальной скоростью будет перпендикуляр в прямоугольном треугольнике:
Скорость, когда относительные скорости равны, будет медианой прямоугольного треугольника:
| Критерии оценивания выполнения задачи | Баллы |
| Правильно записана формула для закона сложения скоростей | 1 |
| Правильно построены треугольники скоростей | 1 |
| Найдены модули скоростей квадрокоптера | 4 |
| Найдены направления движения квадрокоптера | 4 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




