.07 Равноускоренное движение. Векторный подход - Красота
Ошибка.
Попробуйте повторить позже
Увидев с противоположного берега стоящего на высоком краю оврага Леопольда, мыши бросили прямо в него со
скоростью камень. Леопольд заметил это и в момент броска прыгнул со скоростью
в плоскости траектории полета
камня перпендикулярно линии, соединяющей его с мышами (см. рис.). Когда расстояние между Леопольдом и камнем
стало минимальным, их скорости вновь оказались перпендикулярны.
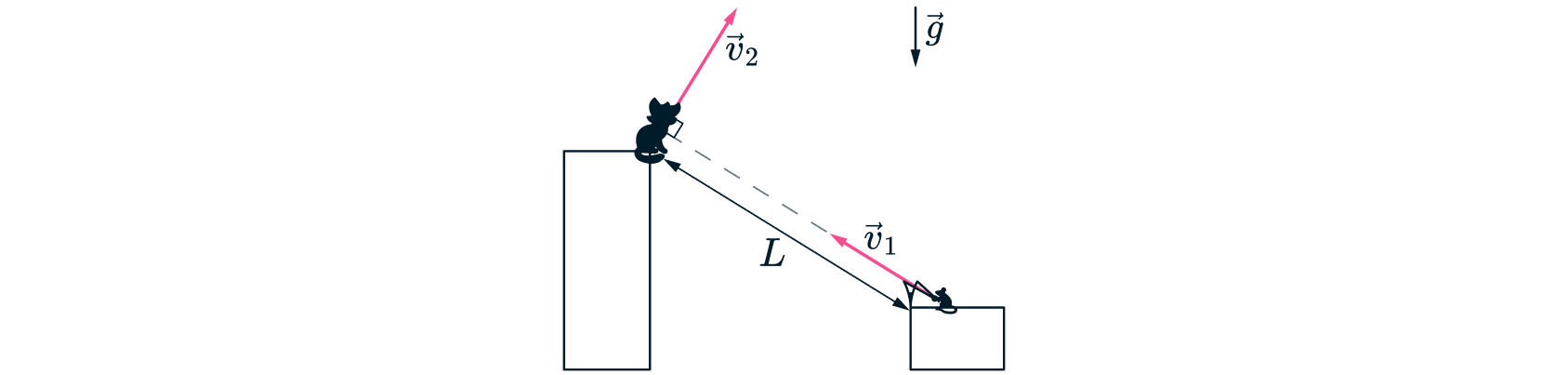
Найдите максимально возможное начальное расстояние между мышами и Леопольдом.
Когда расстояние между Леопольдом и камнем стало минимальным, Леопольда, мышей и камень сфотографировали.
Начальное расстояние между мышами и Леопольдом было максимально возможным. На рисунке точка обозначает
положение Леопольда,
— положение мышей,
— камня в момент снимка. Ориентация фотографии неизвестна. Вы
можете пользоваться линейкой с делениями.
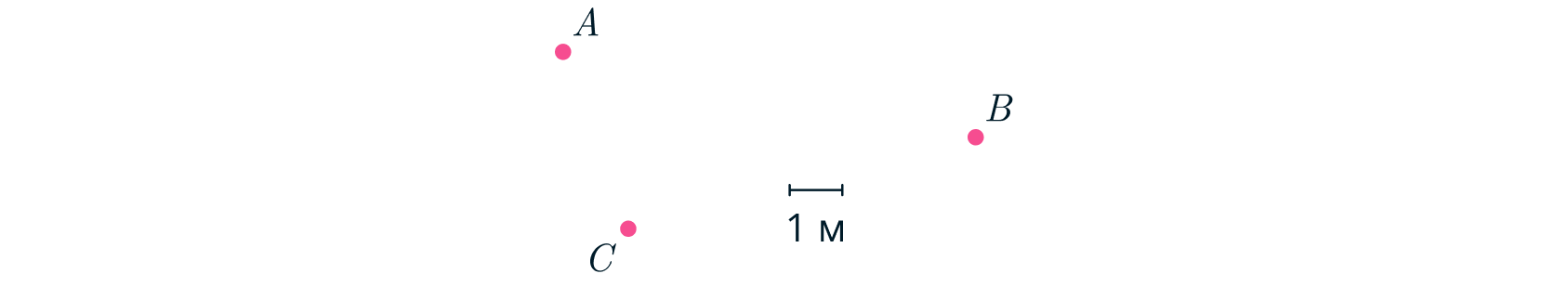
Найдите значения скоростей и
Ускорение свободного падения
Предисловие: Последняя “перестрелка” Леопольда и мышей произошла в 2002 году, с тех пор мыши кота не беспокоили. Спустя 18 лет, в 2020 году, нашлись новые подводные камушки для легендарной рогатки и мыши решили “тряхнуть стариной”. Примечание: в ходе перестрелки никто из животных не пострадал.
В системе отсчёта Леопольда камень движется прямолинейно с постоянной скоростью Расстояние от Леопольда
до камня минимально, когда соединяющий их отрезок перпендикулярен вектору относительной скорости (см. рис.). Из
подобия треугольников определим перемещение камня относительно Леопольда:
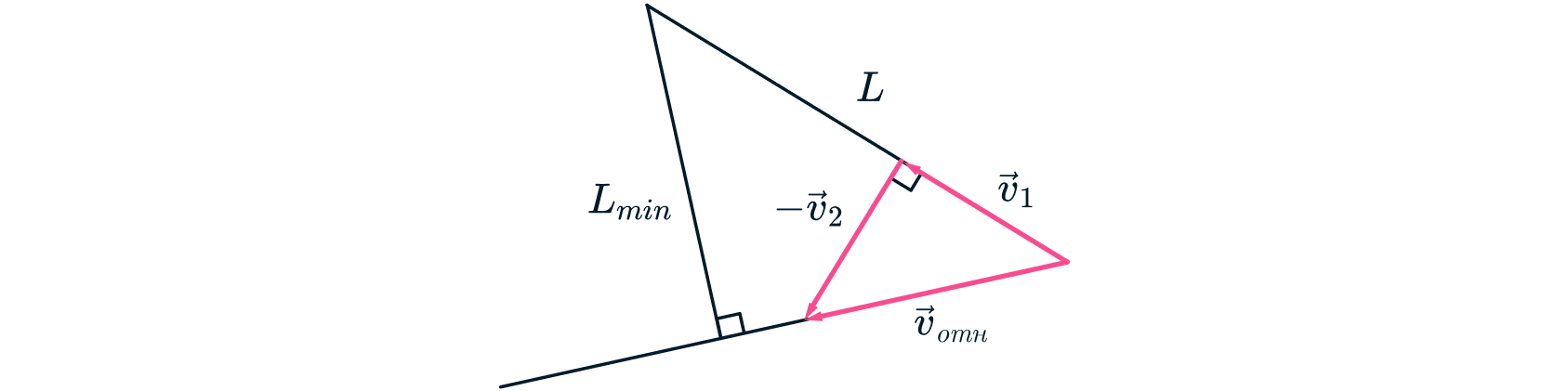
откуда
Найдем максимально возможное время, через которое скорости камня и Леопольда вновь станут перпендикулярны.
Построим треугольники скоростей камня и Леопольда для максимального сближения, объединив их в один
четырёхугольник. Заметим, что этот четырёхугольник можно вписать в окружность, поскольку сумма противоположных
углов равна Диаметр окружности фиксирован и равен
Поскольку
максимально при максимальном
значении
необходимо, чтобы вторая диагональ четырёхугольника, равная
также была максимальна. Это
достигается если
– диаметр данной окружности. Таким образом,
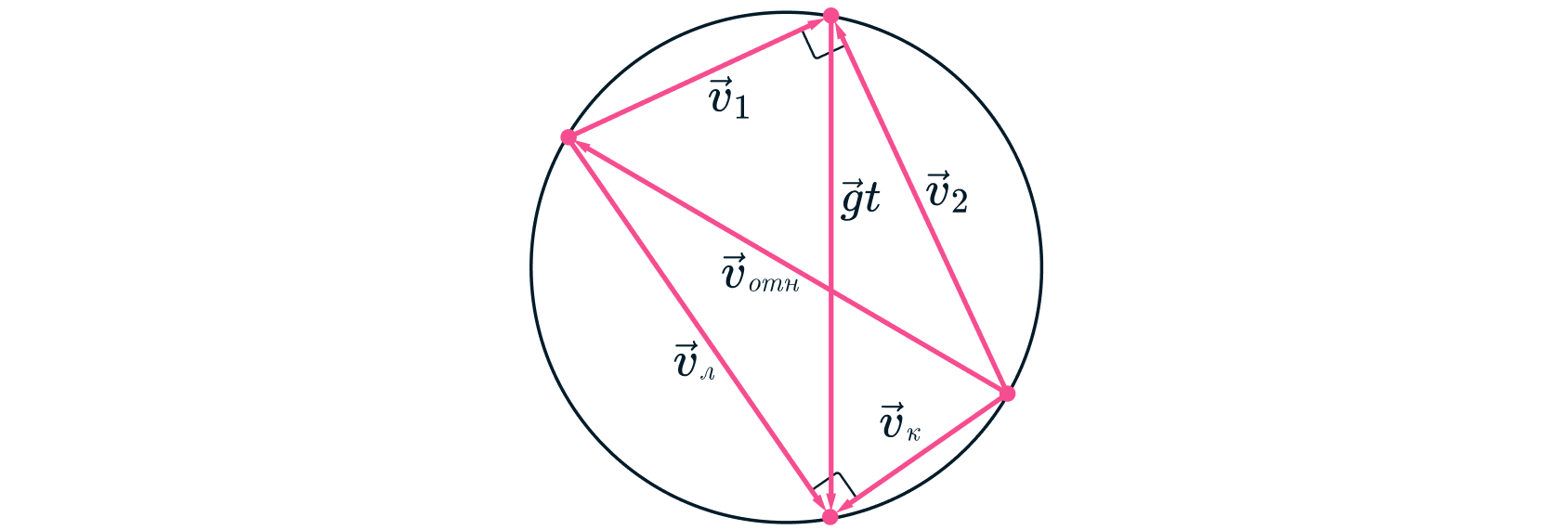
и окончательно:
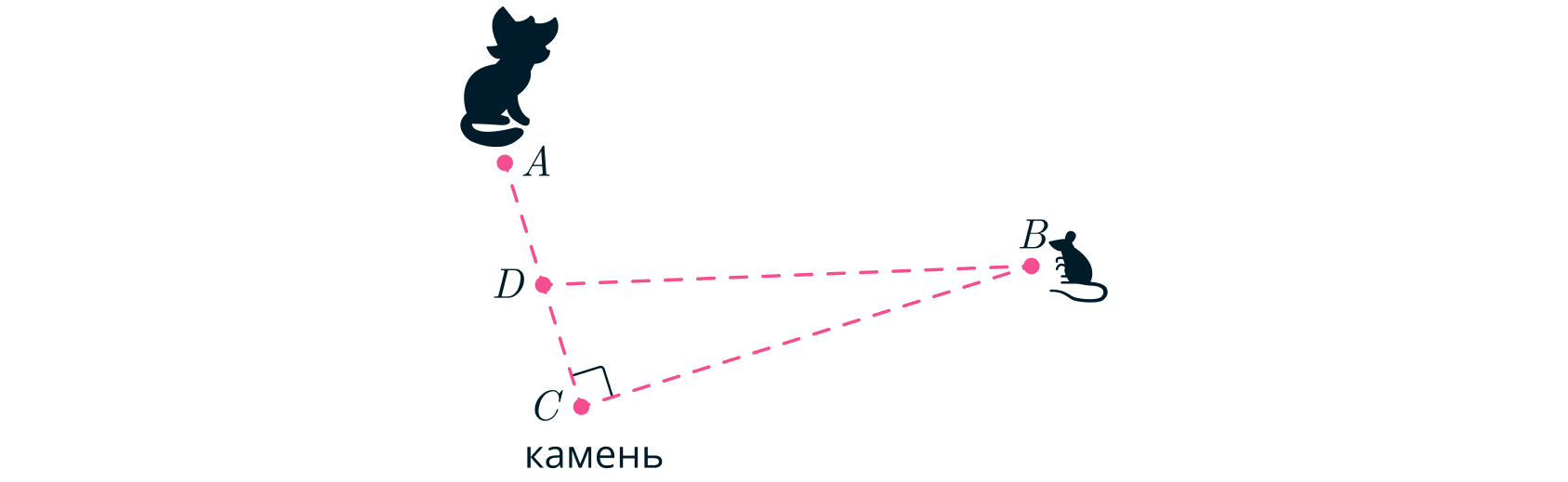
Заметим, что вектор средней скорости камня в момент фотографии равен , в вектор средней скорости
Леопольда
. Это значит, что перемещения камня и Леопольда равны по модулю и противоположны по
направлению. Пусть
- середина отрезка
. Тогда из условия равенства перемещений по модулю следует, что
, а также, что треугольник
- прямоугольный, причём
. Измеряя
и
,
получим
камень
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




