07 Равноускоренное движение. Векторный подход - Красота
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Из отверстия шланга, прикрытого пальцем бьют две струи под углом и
к горизонту с
одинаковой начальной скоростью
. На каком расстоянии по горизонтали струи пересекутся?
Нарисуем треугольники перемещений для соответствующих капель фронтов:
.png)
Из векторного треугольника перемещений видим, что , откуда
.
Из вертикального катета большого треугольника имеем:
откуда подставив , получим
откуда получим
тогда
Ошибка.
Попробуйте повторить позже
Из отверстия шланга, прикрытого пальцем бьют две струи под углом и
к горизонту с
одинаковой начальной скоростью
. На каком расстоянии по горизонтали струи пересекутся?
Нарисуем треугольники перемещений для соответствующих капель фронтов:
.png)
Из векторного треугольника перемещений видим, что , откуда
.
Из вертикального катета большого треугольника имеем:
откуда подставив , получим
откуда получим
тогда
Ошибка.
Попробуйте повторить позже
Тело, брошенное под углом к горизонту, дважды находилось на одной и той же высоте – в момент
времени
и
. Определите эту высоту и начальную скорость
?
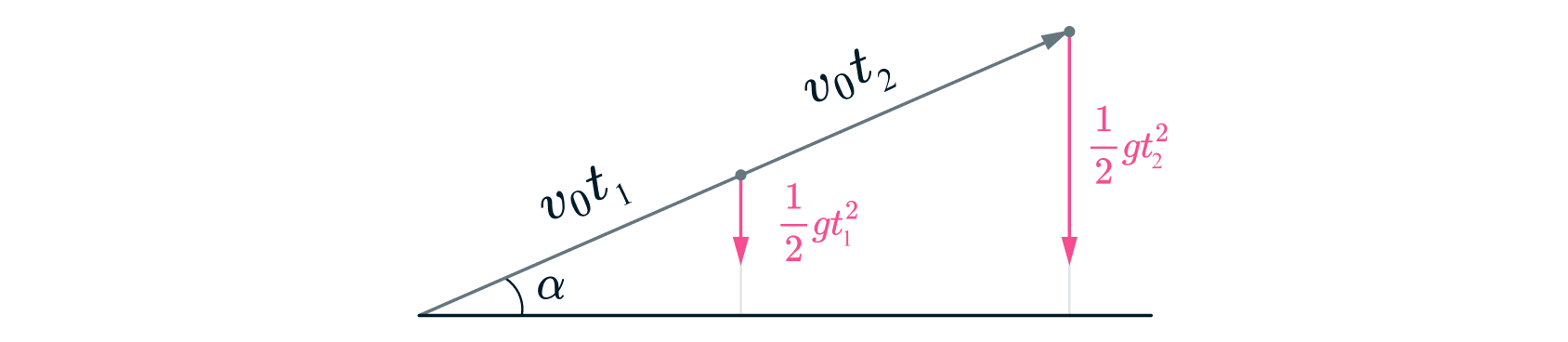
Разберемся со скоростью .
Условие нахождение на одной высоте в моменты времени и
можно интерпретировать с помощью
треугольника перемещений.
Из рисунка мы видим, что с одной стороны , а с другой стороны
(просто определили катеты в двух прямоугольникх треугольниках).
Приравнивая данные выражения, получаем, что , откуда после
несложных математиеских преобразований получаем, что скорость
.
Теперь, зная скорость, несложно определить и высоту, на которой тело проходит через данные времена.
Как было показано,
| Критерии оценивания выполнения задачи | Баллы |
| Использован треугольник перемещений | 2 |
| Записаны выражения для высоты в двух случаях | 3 |
| Получено выражение для искомой скорости | 3 |
| Получено выражение для искомой высоты | 2 |
| Максимальный балл | 10 |
Ошибка.
Попробуйте повторить позже
Из точки A, находящейся на вершине крутого обрыва на высоте над горизонтом, бросают небольшой
предмет в точку B горизонтальной поверхности, находящуюся от обрыва на расстоянии
. Чему равна
минимальная скорость броска? Под каким углом к горизонту должен при этом быть совершен бросок? С
какой скоростью предмет упадет на горизонтальную поверхность? Чему будет равен угол падения на
горизонтальную поверхность?
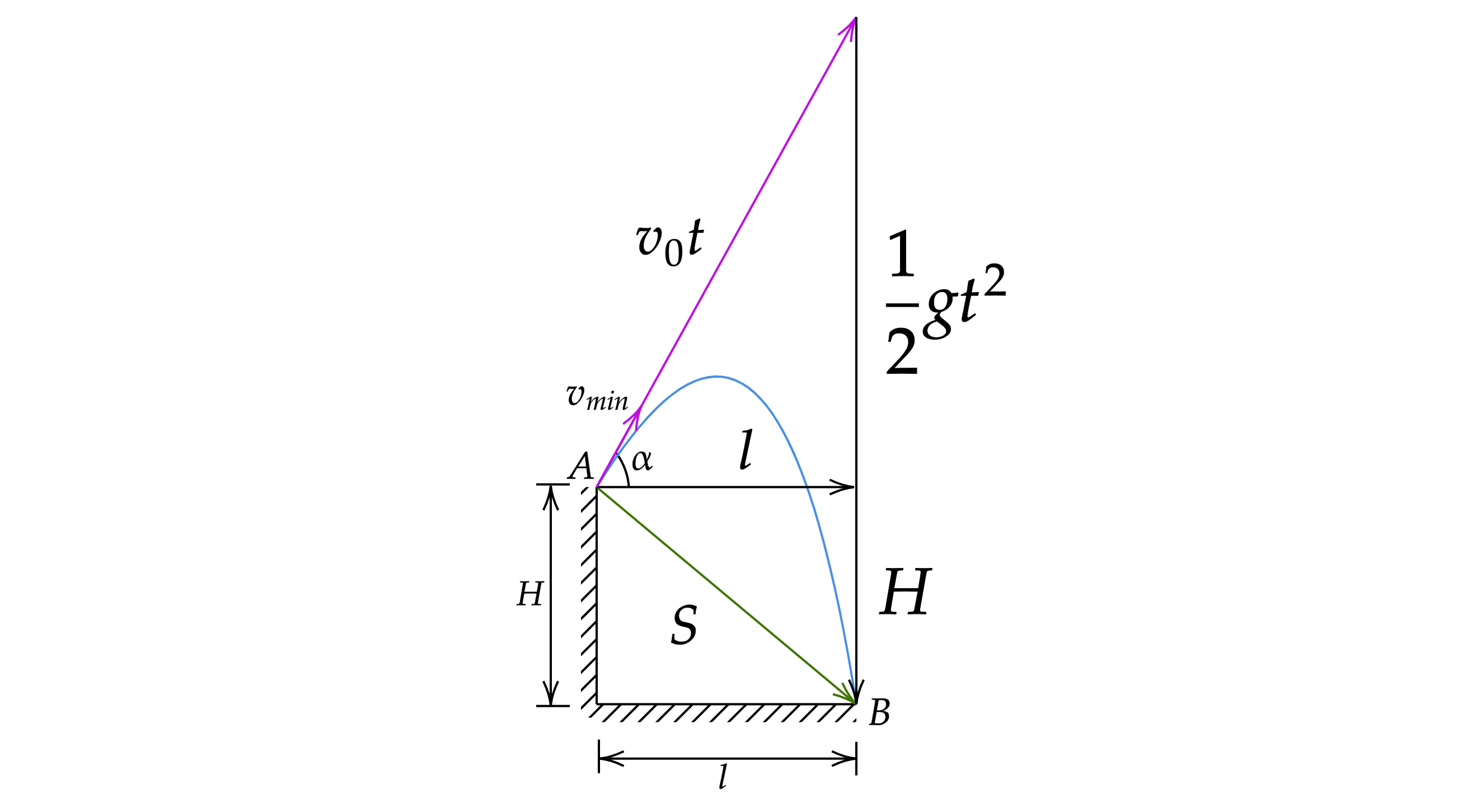
На рисунке - перемещение. Видим, что
Исключим из этих уравнение время, получим квадратное уравнение относительно
Анализ данного уравнение показывает, что при данном полете может реализовываться сразу несколько
ситуация:
1) слишком малое, чтобы долететь до точки В при любом из возможных углов;
2) При дискриминанте =
существует лишь один угол, при котором для заданной скорости
возможно попадание в В;
3) Существует скорость >
, при которой так же возможно попадание в В.
Ясно, что для соблюдения условия задачи необходимо, чтобы дискриминант =
(эквивалентно
при горизонтальном полете), тогда
А угол бросания выражается через тангенс как
Если положить, что =
, то
Теперь определим угол падения. Сделаем это, исходя из закона сохранения энергии. Вначале у тела была как кинетическая, так и потенциальная энергия, а в конце вся она перешла в кинетическую, тогда квадрат конечной скорсти
Таким же образом, как и с углом бросания, используя тригонометрию, определим тангенс угла
падения, из обратимости баллистики :
Не повторяя всех тригонометрических подсчетов, запишем
| Критерии оценивания выполнения задачи | Баллы |
| Использованы формулы кинематики равноускоренного движения | 2 |
| Найдена минимальная скорость бруска | 2 |
| Найден угол броска | 2 |
| Найдена скорость при падении | 2 |
| Найден угол, под которым упадет тело | 2 |
| Максимальный балл | 10 |
Ошибка.
Попробуйте повторить позже
С какой минимальной скоростью надо бросить камешек, чтобы перебросить его через сарай высотой
и шириной
?
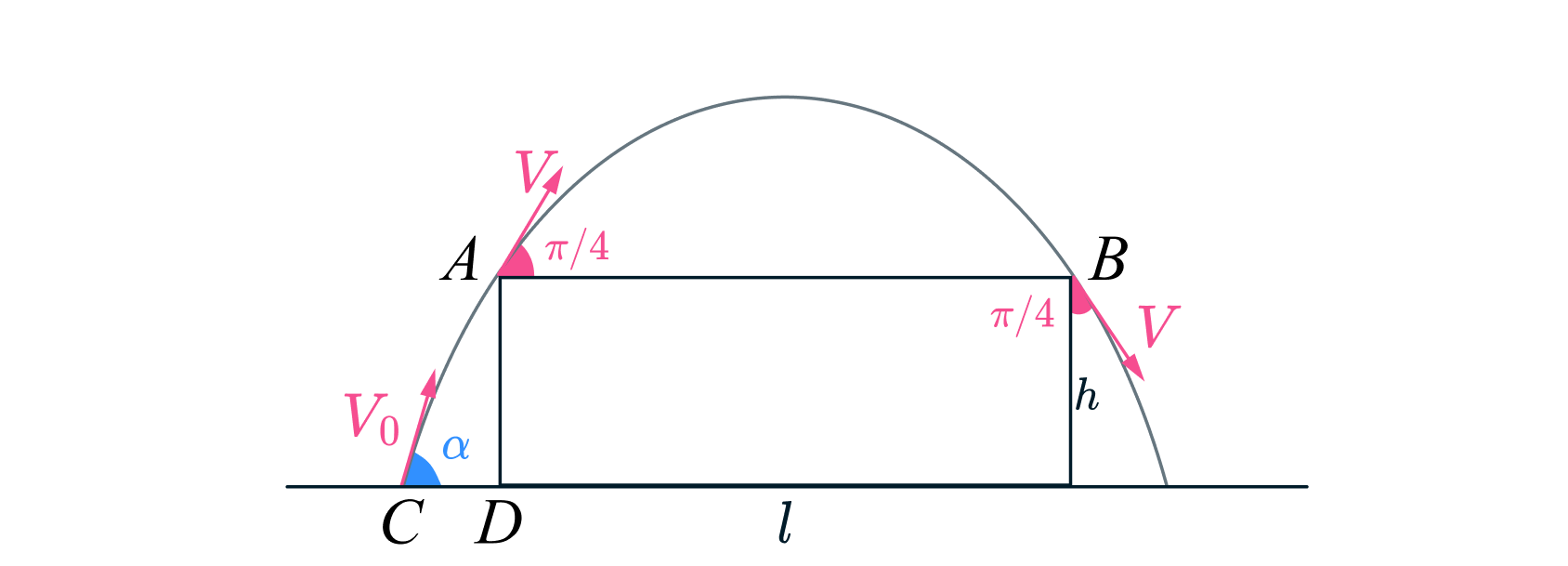
Из соображений симметрии ясно, что траектория мячика, соответствующая минимальной начальной
скорости, имеет вид, показанный на рис. При этом в точке А скорость должна быть направлена под
углом к горизонту, так как тогда дальность полета над сараем будет максимальной. Достигнув этой
точки, мячик должен пролететь расстояние
. Теперь легко найти модуль начальной
скорости
Угол , образуемый вектором
с горизонтом, проще всего найти, учитывая, что
горизонтальная составляющая скорости не меняется при отсутствии сопротивления воздуха:
.
. Под данным углом
необходимо бросить
мячик.
Ошибка.
Попробуйте повторить позже
При какой минимальной начальной скорости можно перебросить камень через дом с покатой крышей
(рис.). Ближайшая стена имеет высоту , задняя стена - высоту
, ширина дома равна
.
.png)
Коль скоро скорость минимальная, то траектория должна проходить через точки вершины трапеции
крыши, причем в вершине, расположенной на высоте полагается минимальная скорость,
необходимая для пролета по данной траектории. Рассмотрим полет из
в
, исходя из обратимости
полета в баллистике это эквивалетно полету из
в
, запишем законы движения по горизонтальной
и вертикальной оси:
Исключив в этих уравнениях время , получим квадратное уравнение относительно
:
Рассмотрим случай (существует одна подходящая траектория):
Теперь запишем ЗСЭ для полета со старта на высоту :
откуда
Ошибка.
Попробуйте повторить позже
Найдите наибольшую дальность полета при броске с высоты с начальной скоростью
. Под каким
углом к горизонту следует осуществить бросок?
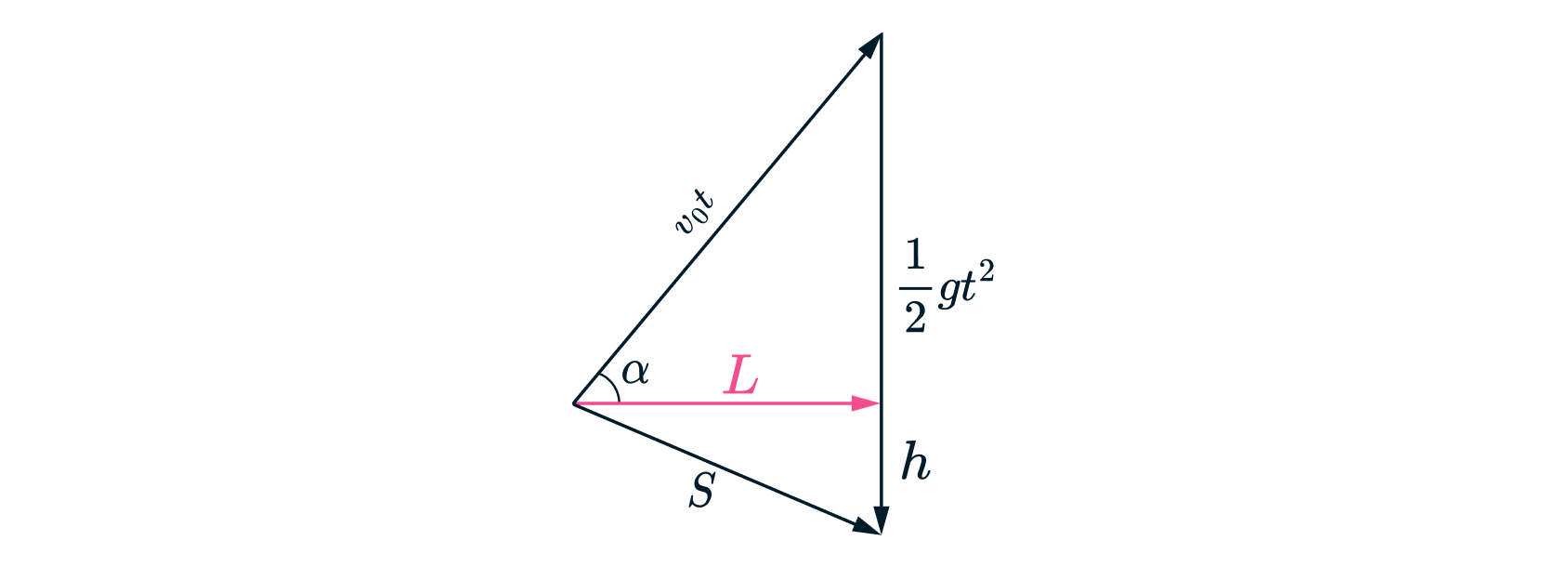
Из векторного треугольника перемещения и теоремы Пифагора следует, что
Взяв производную и пиравняв ее к нулю, определим, при каком времени достигается наибольшая дальность полета:
Подставляя время в начальное выражение, получаем, что
Тангенс угла, при котором следует осуществить бросок определяется следующим образом:
Ошибка.
Попробуйте повторить позже
Какова наибольшая дальность броска вдоль склона с углом наклона к горизонту ? Бросок
производится под уклон. Под каким углом к горизонту надо произвести бросок?
.png)
Из векторного треугольника перемещений и теоремы синусов следует, что ,
откуда время
. Расстояние по горизонтали
Возьмем от производную по углу
:
откуда выражается тангенс угла, под которым совершили бросок относительно плоскости склона:
тогда угол, под которым совершили бросок относительно горизонта, .
Обратите внимание, что бросок происходит по биссектрисе угла между вертикалью и вектором перемещения.
Ошибка.
Попробуйте повторить позже
Какова наибольшая длина простреливаемой области при стрельбе из-за вертикальной стенки
высотой
с начальной скоростью
? Под каким углом к горизонту следует осуществить
выстрел?
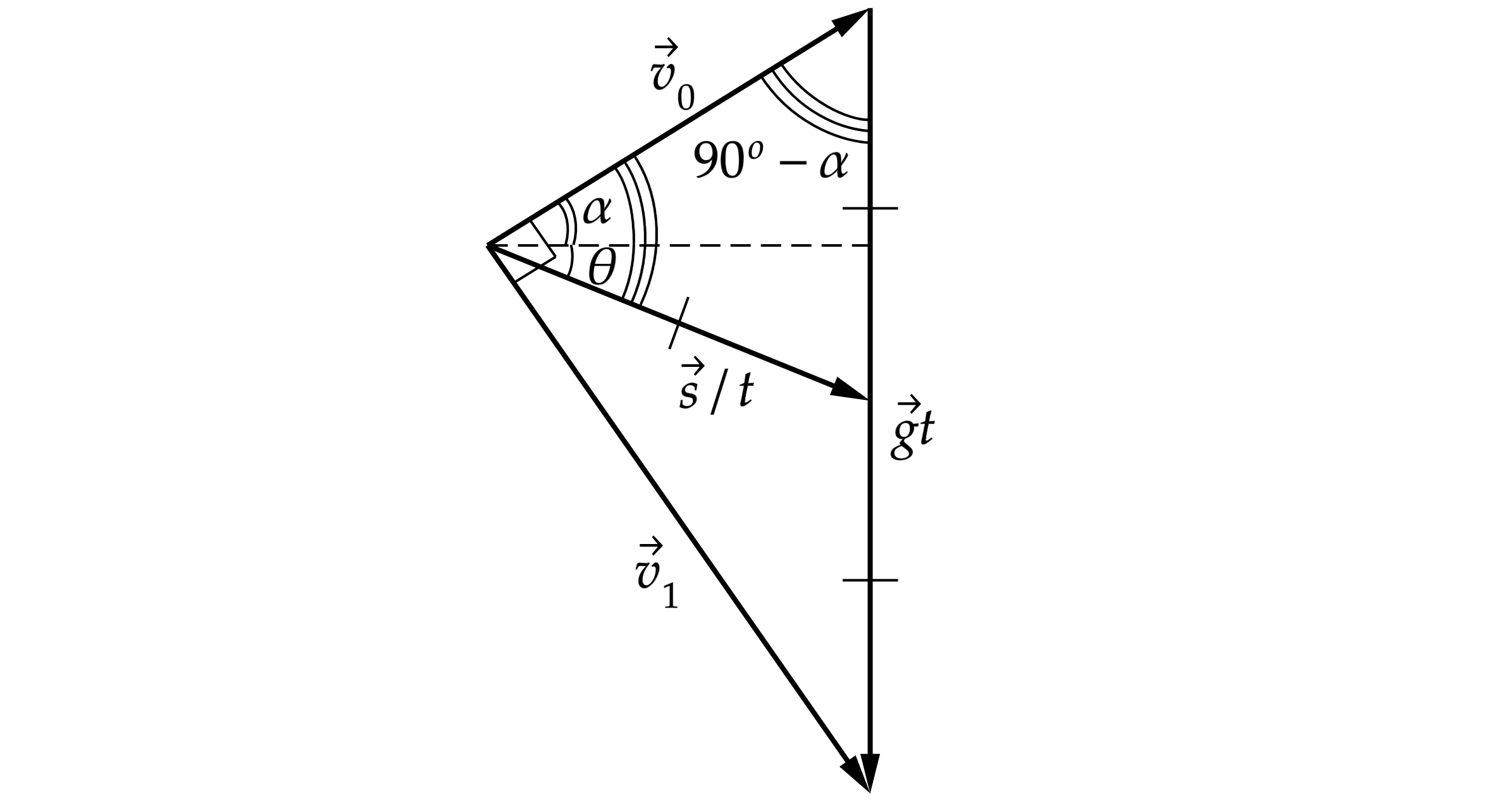
Рассмотрим бросок из-за стенки, чтобы длина простреливаемой области была максимальна, траектория броска должна проходить через вершину стенки. Запишем закон сохранения энергии для участка полета от точки броска до вершины стенки:
где – скорость в вершине стенки. Отсюда:
Пусть скорость направлена под углом
к горизонту. Дальнейший полет аналогичен броску с
вершины стенки со скоростью
под углом
к горизонту. В треугольнике скоростей площадь равна
, т.к.
– высота, а
– сторона, на которую она опущена. С другой стороны площадь равна
, где
– угол между скоростями, а
, поскольку изначальная скорость
броска равна конечной скорости. Отсюда получим выражение для длины простреливаемой
области:
Видно, что дальность максимальна при , т.е. скорости должны быть перпендикулярны.
Тогда из треугольника скоростей можем найти угол
:
Максимальная длина простреливаемой области равна:
| Критерии оценивания выполнения задачи | Баллы |
| Использован закон сохранения энергии | 2 |
| Получено выражение для скорости в вершине стенки | 2 |
| Получено промежуточное выражение для искомой длины | 2 |
| Получены необходимые тригонометрические соотношения | 2 |
| Получено итоговое выражение для искомой длины | 2 |
| Максимальный балл | 10 |
Ошибка.
Попробуйте повторить позже
Школьник бросает мяч в баскетбольное кольцо. Чтобы попасть в цель при броске под углом к горизонту, он
должен сообщить мячу начальную скорость
, а при броске под углом
– начальную скорость
. На какой высоте
над точкой бросания расположено баскетбольное кольцо? Под каким углом
к
горизонту наклонён отрезок, соединяющий точку бросания и кольцо? Бросок каждый раз производится из
одной и той же точки. Сопротивлением воздуха можно пренебречь, ускорение свободного падения равно
.
(МОШ, 2007, 10)
Источники:
Введём систему координат, направив ось горизонтально по направлению к кольцу, а ось
— вертикально вверх.
Совместим начало координат с точкой бросания. Если в качестве начала отсчёта времени выбрать момент броска, то закон
движения мяча, брошенного с начальной скоростью
под углом
к горизонту, запишется следующим
образом:
и
Следовательно, траектория движения тела задаётся
уравнением:
Пусть — координаты кольца; получаем систему уравнений:
Учитывая данные из условия задачи, приводим систему к виду:
Приравнивая эти два соотношения для находим координату
Отсюда и
Официальное решение МОШ
| Критерии оценивания выполнения задачи | Баллы |
| Верно записан закон движения мяча | 2 |
| Получено верное выражение для траектории движения тела | 2 |
| Записана система уравнений с введенными координатами кольца | 2 |
| В системе уравнений учтены данные из условия задачи | 2 |
| Получены верные выражения для | 2 |
| Максимальный балл | 10 |
Ошибка.
Попробуйте повторить позже
Лампоча висит на расстоянии от потолка и на высоте
от пола. При её разрыве осколки
разлетаются во все стороны с одной и той же скорость
. Найти радиус
круга на полу, в который
попадут осколки. Считать, что удары осколков о потолок абсолютно упругие, а об пол – неупругие. До
стен осколки не долетают
Предположим сначала, что потолок отсутствует, и найдем в этом случае максимальный радиус пятна на
полу, в котором лежат осколки. Введем систему координат с началом, совпадающим с патроном
лампочки. Условия падения на землю через время осколка, вылетевшего под углом
к горизонту,
таковы:
Знак минус определен из-за того, что система координаты, выбранная в данной задаче, направлена
вверх по вертикали и вправо по горизонтали.
Очевидно, нам необходимо так подобрать угол , чтобы величина
была максимальной.
Преобразуем для этого первое уравнения к виду
, а второе к виду
,
откуда
тогда .
Пусть время полета осколка на такое расстояние, тогда угол вылета к горизонту найдем из
уравнения
.
Высоту этой траектории над уровне лампочки найдем по формуле:
Вспомним теперь про потолок, Очевидно, если больше или равен
, то
.
В случае, когда , т.е.
. максимальный радиус пятна на полу получится от осколков, у
которых максимальная высота траектории (над уровнем патрона) равна
(их траектория будет
касательной к потолку). Чтобы доказать это, достаточно рассмотреть хотя бы один осколок,
отразившийся от потолка. Уровень патрона после отражения он пересечет под углом вылета.
Следовательно, траектория этого осколка будет более крутой по сравнению с «касательной»
траекторией, и они никогда не пересекутся. Значит, осколок, коснувшийся потолка, пролетит по
горизонтали дальше всех остальных, ударившихся о потолок. Осколки, не долетевшие до
потолка, при своем движении до земли не могут пересечь «касательной» траектории
Ошибка.
Попробуйте повторить позже
Кот Леопольд стоял у края крыши сарая. Два злобных мышонка выстрелили в него из рогатки. Однако
камень, описав дугу, через упруго отразился от наклонного ската крыши сарая у самых лап
кота и через
попал в лапу стрелявшего мышонка (см. рисунок). На каком расстоянии
от
мышей находился кот Леопольд?
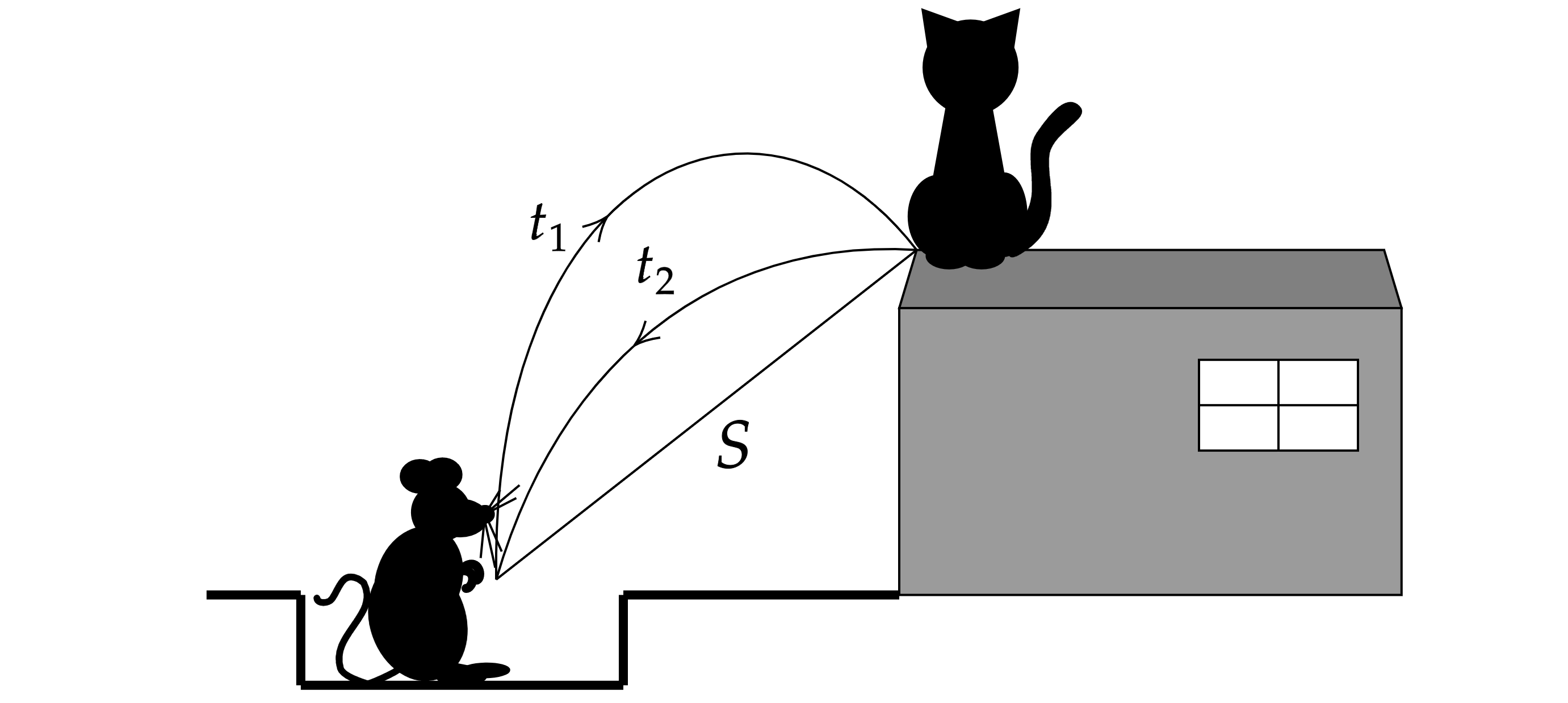
Изобразим полет камня к Леопольду и обратно
.png)
Нарисуем треугольники скоростей для полетов туда и обратно
.png)
.png)
Камень упруго отразился, следовательно, конечная скорость первого участка равна начальной
скорости для второго участка . С другой стороны поскольку обратно камень летит в точку
броска изменение потенциальной энергии такое же как при броске туда. Потерь кинетической энергии
при полете нет, значит кинетическая энегрии в конечной точкетакая же, как при броске из точки старта.
Отсюда
. Рассмотрим треугольники
и
. Площадь треугольника скоростей
пропорциональна
(высота
, сторона
), поскольку дальности при броске туда и обратно
равны, то равны и площади соответствующих треугольников скоростей. Медиана в треугольнике делит
его на два равновеликих, учитвая, что площади треугольников скоростей равны, то равны и площади
треугольников
,
,
,
. Теперь рассмотрим треугольники
и
. Они
имеют равны стороны(
), равные углы(векторы перемещений туда и обратно параллельны и
составляют равные углы с вертикалью) и равные площади, а значит и равные высоты. Такие
треугольники явлются равными(можно доказать при помощи "рельс Евклида"), значит
,
откуда получаем:
| Критерии оценивания выполнения задачи | Баллы |
| Верно записан закон движения мяча | 2 |
| Сказано про равенство скоростей после абсолютно упругого удара | 2 |
| Записано равенство скоростей | 2 |
| Нарисованы треугольники скоростей | 2 |
| Получены верные выражения для | 2 |
| Максимальный балл | 10 |
Ошибка.
Попробуйте повторить позже
Кот Леопольд сидел на самом краю крыши сарая. Два озорных мышонка решили выстрелить в него из рогатки, но кот
заметил их и решил отстреливаться. Камни из рогаток мышат и кота вылетели одновременно и столкнулись в середине
отрезка (см. рисунок). Найдите высоту
сарая и отношение пути, пройденного камнем кота Леопольда, к пути,
пройденному камнем мышат, если известно, что
скорость камня, вылетевшего из рогатки мышат,
а
кот выстрелил горизонтально.
(Всеросс., 2002, финал, 10)
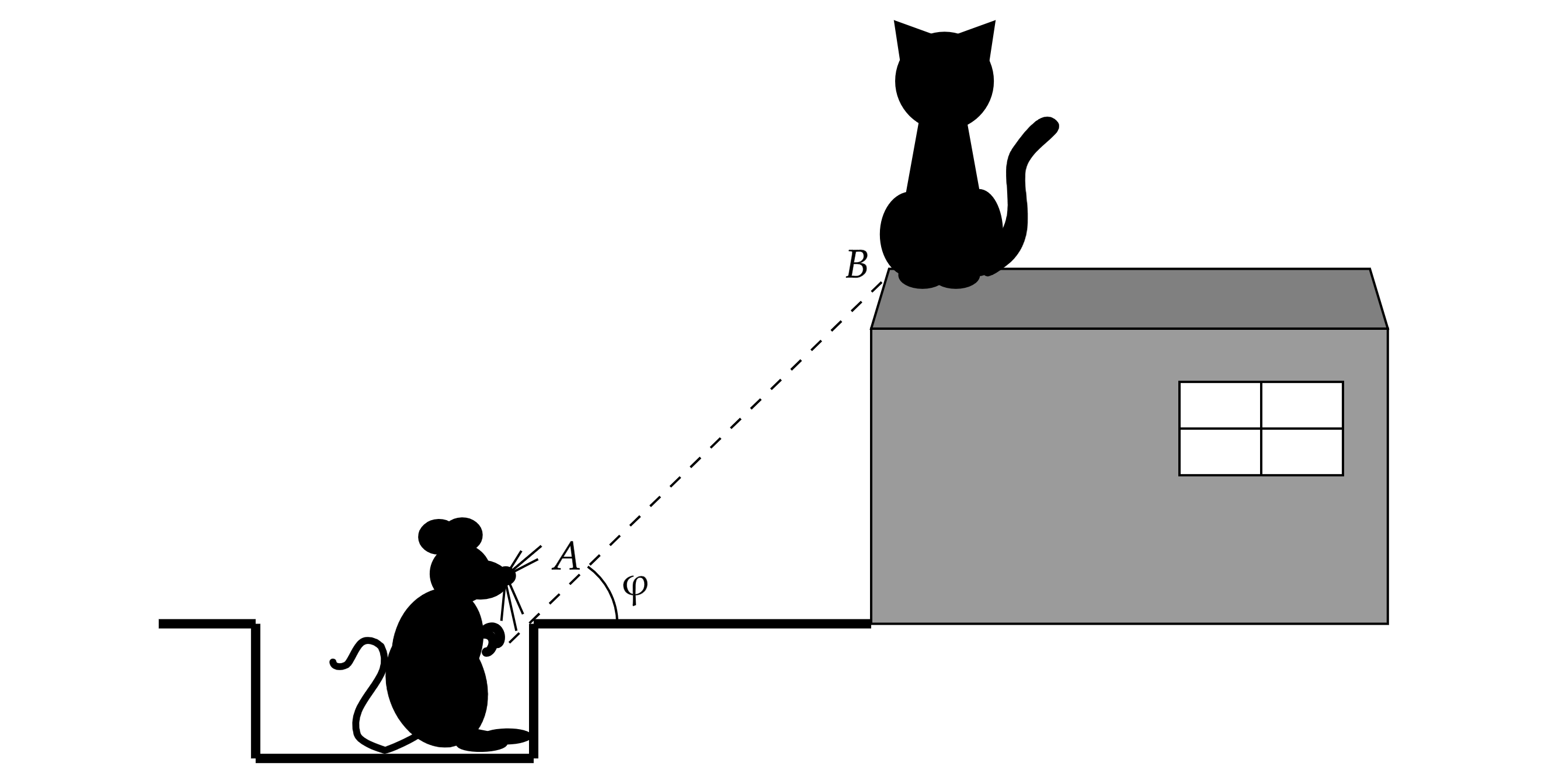
Источники:
Сделаем рисунок. Пусть – скорость камня Леопольда,
– время полета камней.
.png)
Рассмотрим тангенсы углов и
:
Поскольку , то:
С одной стороны , в то же время
, тогда:
Из труегольника :
Подставляя , получим:
Поделив полученное выражение пополам, заметим, что выражение для является формулой максимальной высоты
полета, значит в точке столкновения скорость камня мышат горизонтальна, как и начальная скорость камня Леопольда,
поскольку бросок в баллистике обратим, если докажем, что начальная скорость камня Леопольда и скорость в точке
столкновения камня мышат равны, то будут равны и их пути. Запишем векторные уравнения для перемещений
камней:
Сложив уравнения, получим:
Что и требовалось доказать, значит:
Ошибка.
Попробуйте повторить позже
При осаде древней крепости осаждённые вели стрельбу по наступающему противнику с помощью катапульт из-за
крепостной стены высотой . Начальная скорость снарядов
. На каком максимальном расстоянии
от стены находились цели, которых могли достигать снаряды катапульт? Сравните это расстояние с максимальной
дальностью
снаряда катапульты. Сопротивлением воздуха можно пренебречь.
(Всеросс., 2004, финал, 9)
Источники:
Максимульную дальность полета обеспечивает единственная траектория, которая проходит над самой вершиной стены.
Эта траектория соответствует броску под некоторым углом к горизонту. Запишем зависимость координат
и
от
времени. Будем считать, что моменту времени
соответствует положение снаряда над самой вершиной
стены:
Свяжем и
и избавимся от времени:
Зафиксируем дальность полета и запишем уравнение
для угла
, который этой дальности соответствует.
Применим также тригонометрическое соотношение
Учтем также, что при координата
нулевая:
Полученное квадратное уравнение таково, что случаю соответствует совпдаение корней этого уравнения, так
как максмальной дальности соответствует единственная траектория. Приравняв к нулю дискриминант данного уравнения,
получаем, что
м. Максимальная же дальность соответсвует случаю, когда
, т.е.
м.
Ошибка.
Попробуйте повторить позже
Пассажирский поезд длиной стоял на первом пути. В последнем вагоне сидел Дядя Фёдор (герой книги Э.
Успенского «Каникулы в Простоквашино») и ожидал письмо, которое ему должен был передать Шарик от кота
Матроскина. В тот момент, когда поезд тронулся, на привокзальной площади, как раз напротив первого вагона,
появился Шарик (рис.). Он определил, что расстояние до последнего вагона равно
. С какой минимальной
скоростью
должен бежать пёс, чтобы передать письмо, если поезд движется с постоянным ускорением
?
(Всеросс., 2007, финал, 9)
.png)
Источники:
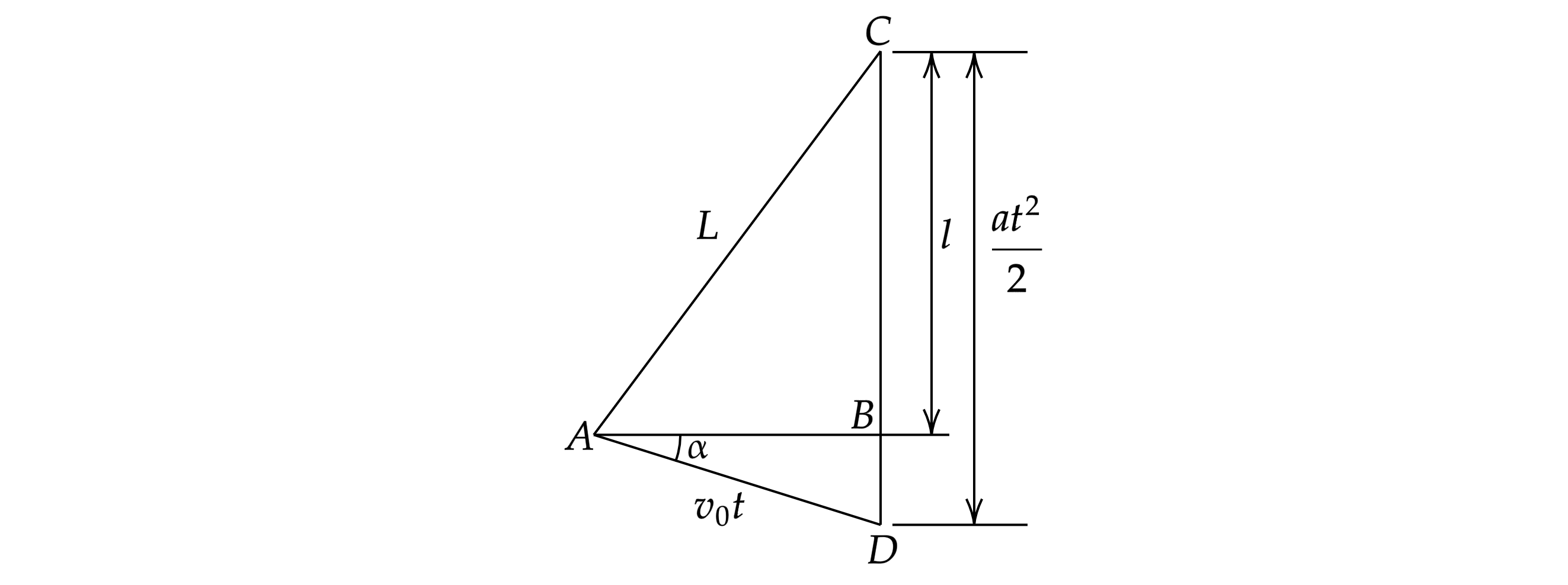
Пусть встреча Шарика с последним вагоном произошла в точке (рис.).Треугольники
АВС и ABD - прямоугольные. Тогда, используя теорему Пифагора, можно записать: ,
что эквивалентно
, откуда квадарат начальной скорости
. Для того чтобы
скорость
была минимальной, необходимо, чтобы сумма
принимала минимальное значение. Используем
неравенство о средних:
откуда . Обратим внимание на то, что минимальная скорость достигается при условии
откуда . Тогда
, значит
- равнобедренный, а
Получили, что Шарику следует бежать под углом
к AB со скоростью .
Ошибка.
Попробуйте повторить позже
Кот Леопольд сидел у края крыши. Два злобных мышонка выстрелили в него из рогатки. Однако камень, описав дугу, упал
у ног кота (см. рисунок) через время . На каком расстоянии
от мышей находился кот Леопольд, если
известно, что векторы скоростей камня в момент выстрела и в момент падения были взаимно перпендикулярны?
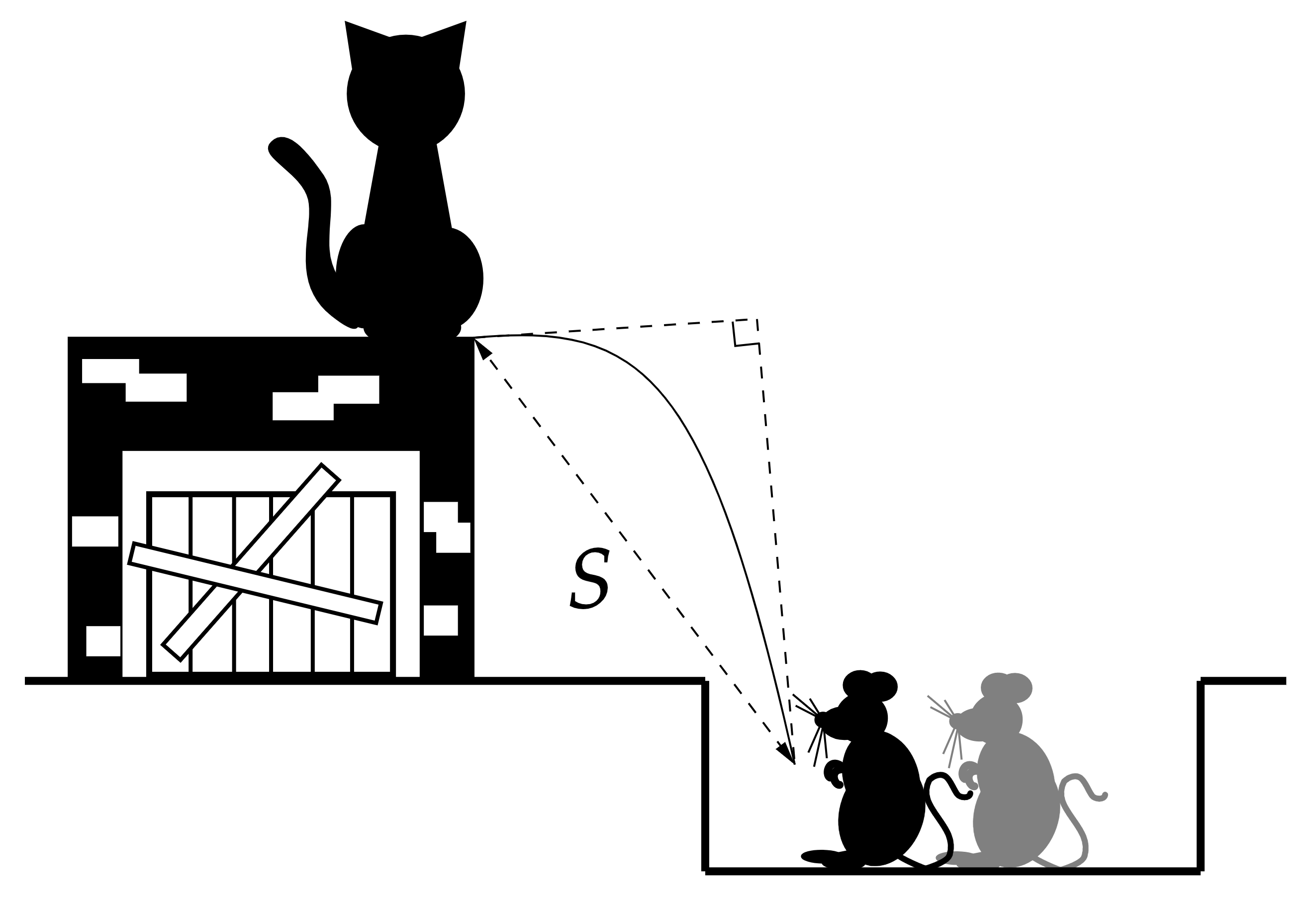
Нарисуем треугольник скоростей и отобразим на нем медиану, которая является отношением перемещения к времени полета:
Поскольку медиана в прямоугольном треугольнике равна половине гипотенузы, получаем:
Отсюда:
Ошибка.
Попробуйте повторить позже
Увидев с противоположного берега стоящего на высоком краю оврага Леопольда, мыши бросили прямо в него со
скоростью камень. Леопольд заметил это и в момент броска прыгнул со скоростью
в плоскости траектории полета
камня перпендикулярно линии, соединяющей его с мышами (см. рис.). Когда расстояние между Леопольдом и камнем
стало минимальным, их скорости вновь оказались перпендикулярны.
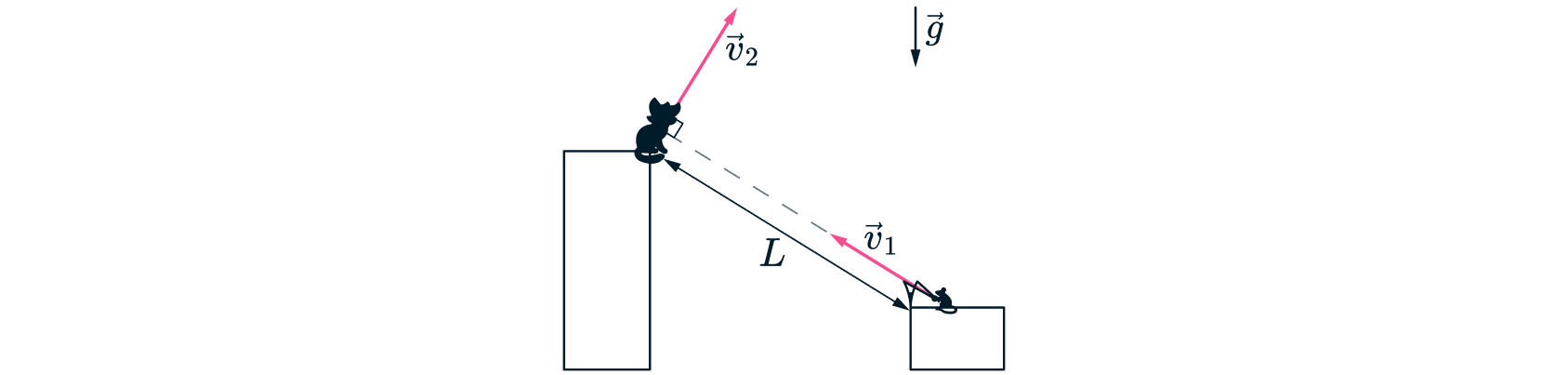
Найдите максимально возможное начальное расстояние между мышами и Леопольдом.
Когда расстояние между Леопольдом и камнем стало минимальным, Леопольда, мышей и камень сфотографировали.
Начальное расстояние между мышами и Леопольдом было максимально возможным. На рисунке точка обозначает
положение Леопольда,
— положение мышей,
— камня в момент снимка. Ориентация фотографии неизвестна. Вы
можете пользоваться линейкой с делениями.
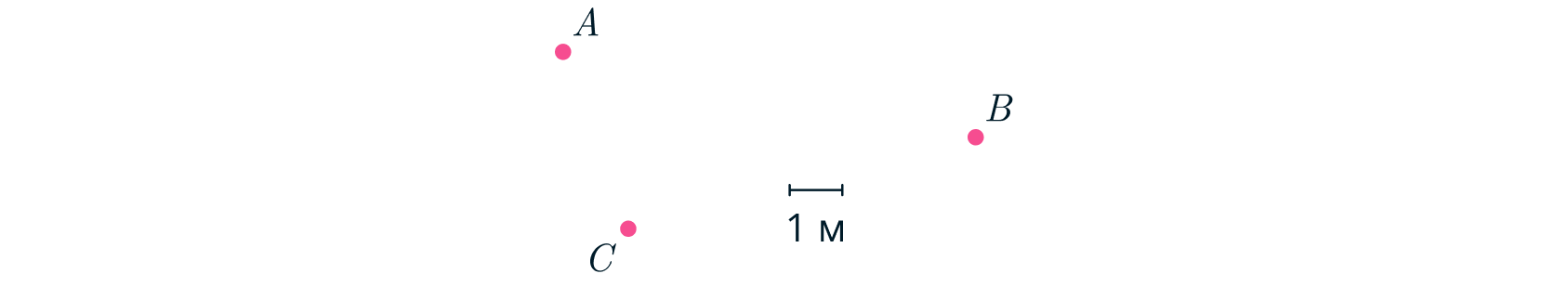
Найдите значения скоростей и
Ускорение свободного падения
Предисловие: Последняя “перестрелка” Леопольда и мышей произошла в 2002 году, с тех пор мыши кота не беспокоили. Спустя 18 лет, в 2020 году, нашлись новые подводные камушки для легендарной рогатки и мыши решили “тряхнуть стариной”. Примечание: в ходе перестрелки никто из животных не пострадал.
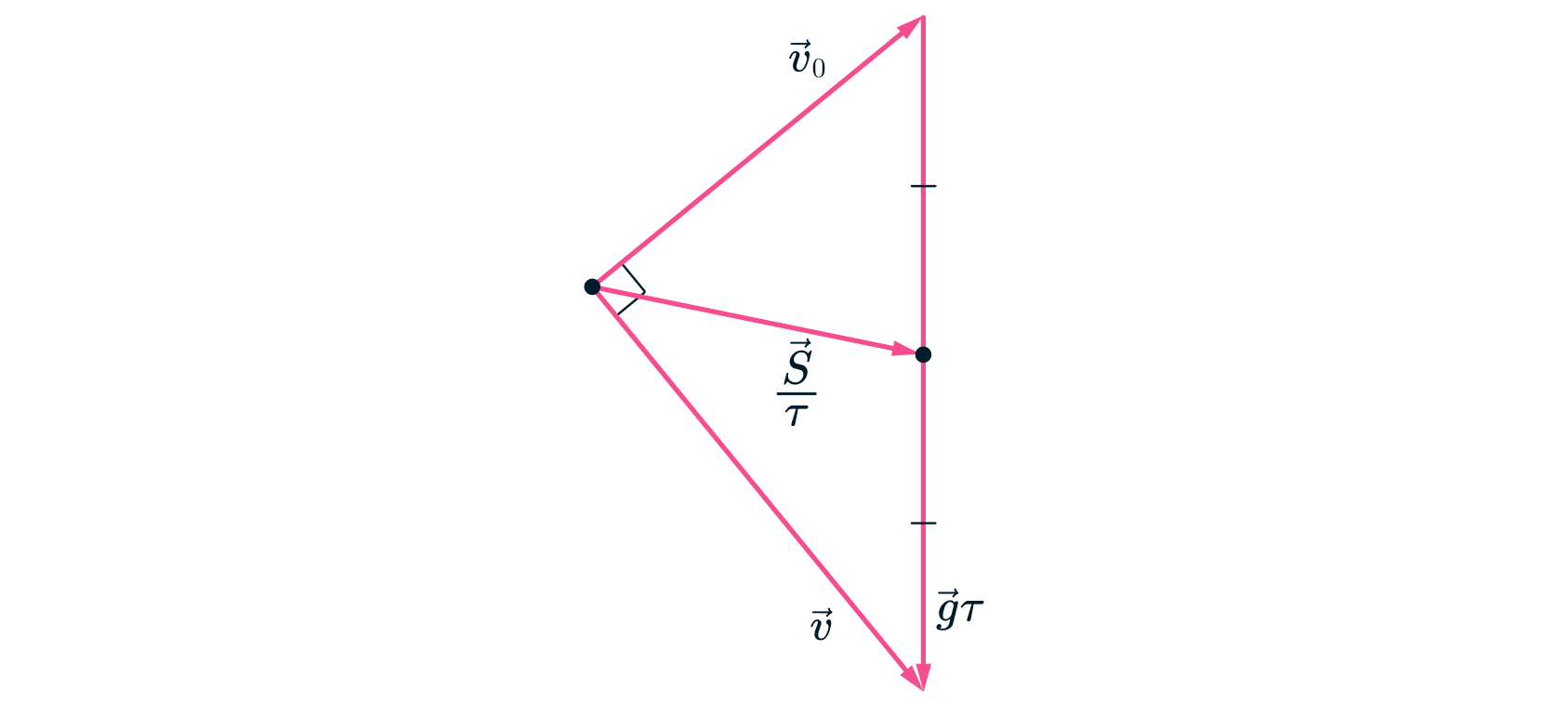
В системе отсчёта Леопольда камень движется прямолинейно с постоянной скоростью Расстояние от Леопольда
до камня минимально, когда соединяющий их отрезок перпендикулярен вектору относительной скорости (см. рис.). Из
подобия треугольников определим перемещение камня относительно Леопольда:
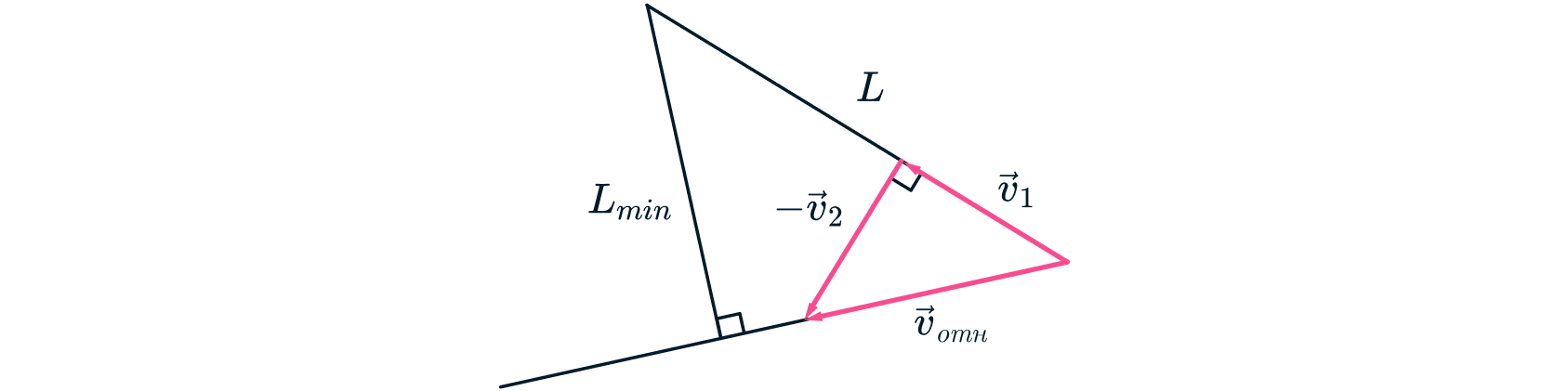
откуда
Найдем максимально возможное время, через которое скорости камня и Леопольда вновь станут перпендикулярны.
Построим треугольники скоростей камня и Леопольда для максимального сближения, объединив их в один
четырёхугольник. Заметим, что этот четырёхугольник можно вписать в окружность, поскольку сумма противоположных
углов равна Диаметр окружности фиксирован и равен
Поскольку
максимально при максимальном
значении
необходимо, чтобы вторая диагональ четырёхугольника, равная
также была максимальна. Это
достигается если
– диаметр данной окружности. Таким образом,
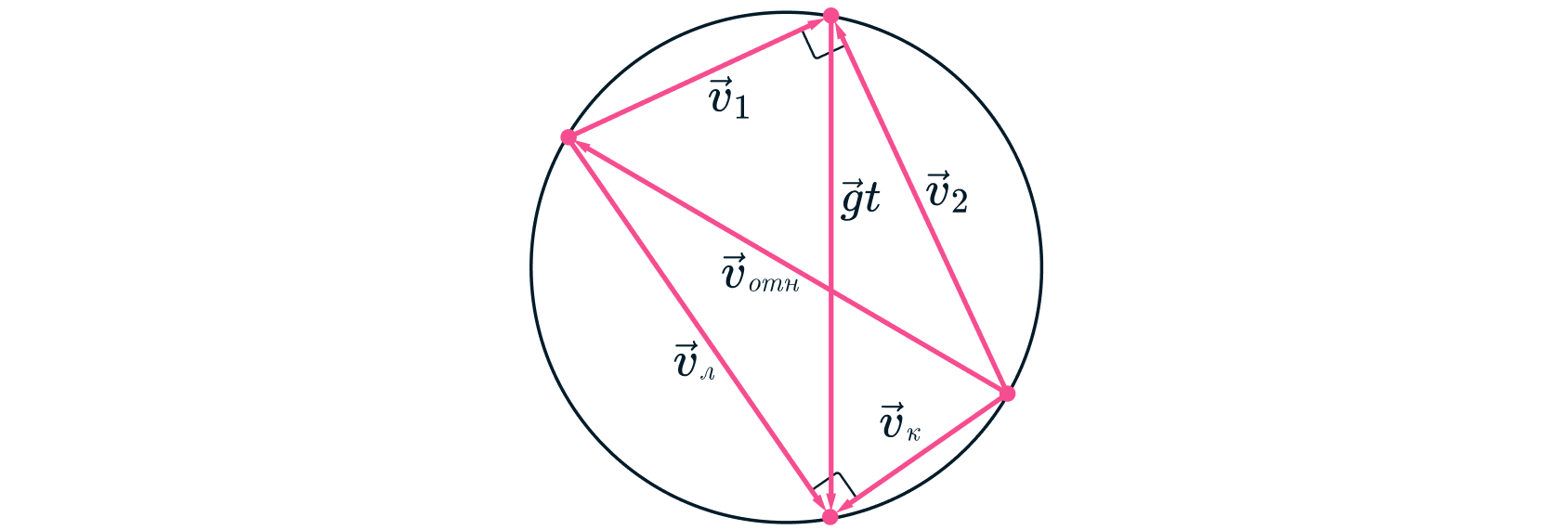
и окончательно:
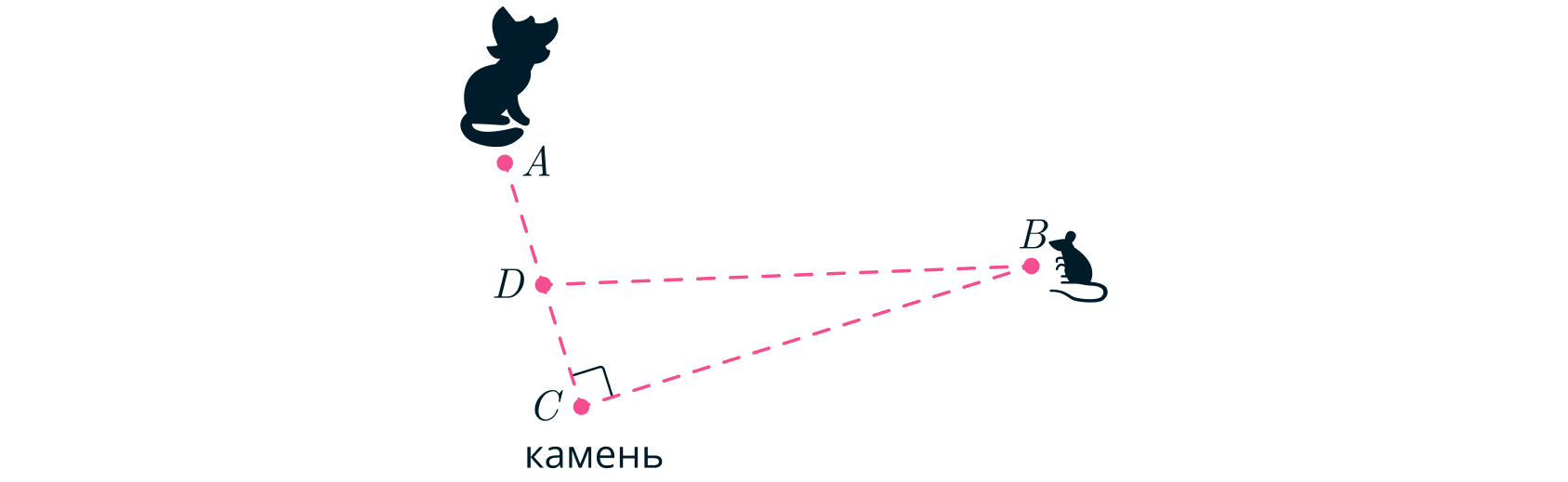
Заметим, что вектор средней скорости камня в момент фотографии равен , в вектор средней скорости
Леопольда
. Это значит, что перемещения камня и Леопольда равны по модулю и противоположны по
направлению. Пусть
- середина отрезка
. Тогда из условия равенства перемещений по модулю следует, что
, а также, что треугольник
- прямоугольный, причём
. Измеряя
и
,
получим
камень
Ошибка.
Попробуйте повторить позже
Пружину «слинки» удерживают за верхний виток так, что ее нижний виток находится на высоте над уровнем
пола, а длина самой пружины, растянутой силой собственного веса, равна
Пружину отпускают. Через какое
время
она упадет на пол? В нерастянутом состоянии витки пружины плотно прилегают друг к другу, не оказывая при
этом давления друг на друга, а длина пружины составляет
Витки тонкие. При схлопывании пружины витки
между собой соударяются неупруго, и к моменту падения она успевает схлопнуться. Ответ дать с точностью

(Всеросс., 2016, ЗЭ, 11)
Источники:
1. Разобъем пружины на витки массой и жесткостью
деформация каждой -
Тогда на
ый виток действует
сила упругости
а на витки, следующие за
ым действует сила тяжести, равная
. В положении
равновесия эти силы равны по модулю.
.png)
Запишем теорему о движении центра масс:
Для системы внешними силами является сила тяжести, поэтому
Получается, что центр массы системы движется с ускорением, равным ускорению свободного падения. Поэтому, для
ответа на вопрос задачи, достаточно понять, на каком расстоянии распологается центр масс пружинки . Тогда искомое
время
выразится как
2. По определению, положение центра массы вычисляется по формуле
Теперь необходимо понять, как выразить сумму в числителе. Координату любого -го элемента пружины можно
выразить как сумму смещений элементов, распологающихся под
ым.
.png)
Воспользуемся теперь условием равновесия, сформулированным выше:
Возвращаемся к выражению для и, пользуясь формулой суммы
первых членов арифметической прогрессии,
получаем
3. Теперь вернемся к вычислению координаты центра масс
Сложность заключается в том чтобы понять, как просуммировать частичную сумму ряда, состоящего из
квадратов натуральных чисел . Для того, чтобы это понять, посчитаем сначала следующие частичные
суммы
при суммировании нулевой степени получили многочлен первой степени по N;
при суммировании первой степени получили многочлен второй степени по N , логично
предположить, что суммирование вторых степеней
даст полином третьей степени. То есть общий вид суммы будет
следующим
Составим систему уравнений и найдем константы
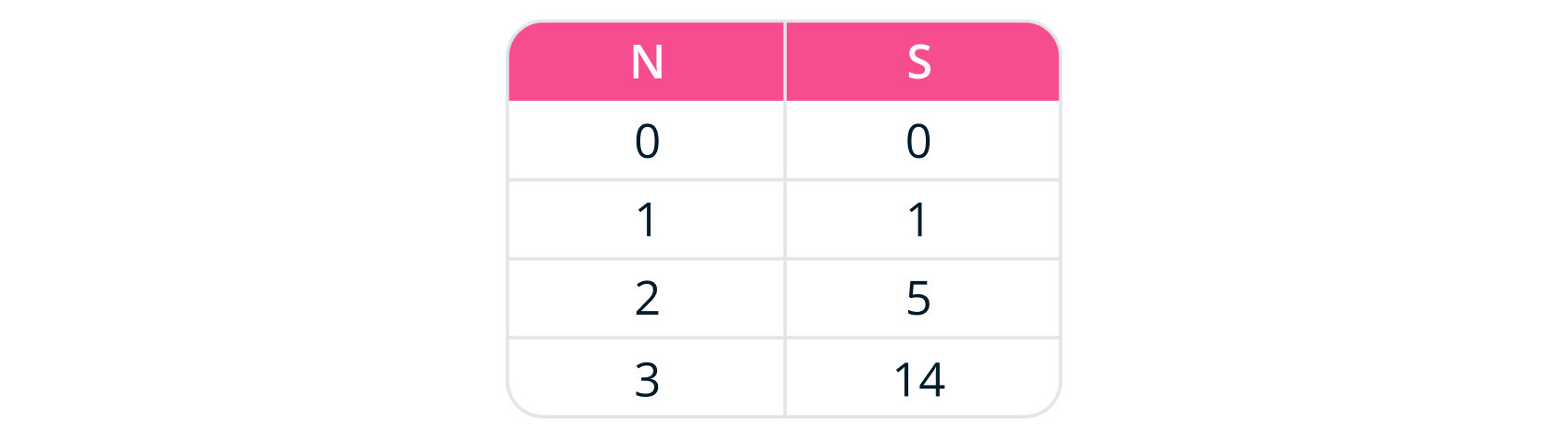
Из системы
Тогда
и для координаты центра масс окончательно получаем (пренебрегая младшими порядками по ):
4. Найдем . Для этого вспомним связь
и, принебрегая младшими порядками по i запишем связь длины
пружины и числа витков:
Теперь получаем ответ на задачу
Пренебрежем членом и оценим погрешность полученного ответа



