.07 Равноускоренное движение. Векторный подход - Красота

1. Разобъем пружины на витки массой и жесткостью деформация каждой - Тогда на ый виток действует сила упругости а на витки, следующие за ым действует сила тяжести, равная . В положении равновесия эти силы равны по модулю.

Запишем теорему о движении центра масс:

Для системы внешними силами является сила тяжести, поэтому

Получается, что центр массы системы движется с ускорением, равным ускорению свободного падения. Поэтому, для ответа на вопрос задачи, достаточно понять, на каком расстоянии распологается центр масс пружинки . Тогда искомое время выразится как

2. По определению, положение центра массы вычисляется по формуле

Теперь необходимо понять, как выразить сумму в числителе. Координату любого -го элемента пружины можно выразить как сумму смещений элементов, распологающихся под ым.

Воспользуемся теперь условием равновесия, сформулированным выше:

Возвращаемся к выражению для и, пользуясь формулой суммы первых членов арифметической прогрессии, получаем

3. Теперь вернемся к вычислению координаты центра масс

Сложность заключается в том чтобы понять, как просуммировать частичную сумму ряда, состоящего из квадратов натуральных чисел . Для того, чтобы это понять, посчитаем сначала следующие частичные суммы

при суммировании нулевой степени получили многочлен первой степени по N;

при суммировании первой степени получили многочлен второй степени по N , логично предположить, что суммирование вторых степеней даст полином третьей степени. То есть общий вид суммы будет следующим

Составим систему уравнений и найдем константы

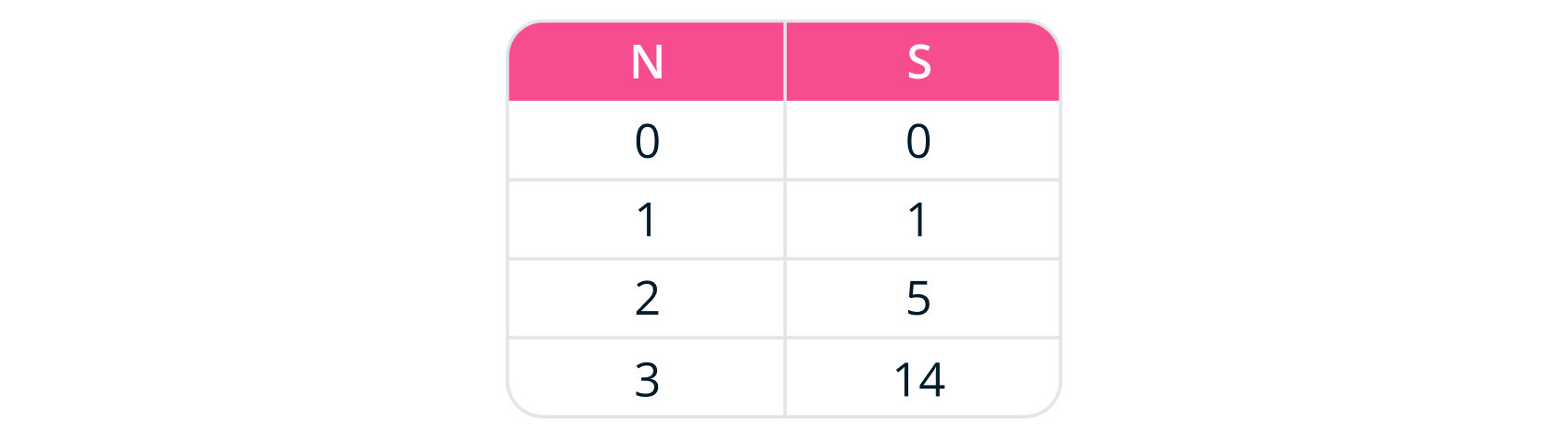
Из системы

Тогда

и для координаты центра масс окончательно получаем (пренебрегая младшими порядками по ):

4. Найдем . Для этого вспомним связь и, принебрегая младшими порядками по i запишем связь длины пружины и числа витков:

Теперь получаем ответ на задачу

Пренебрежем членом и оценим погрешность полученного ответа