.07 Равноускоренное движение. Векторный подход - Красота
Ошибка.
Попробуйте повторить позже
Из точки A, находящейся на вершине крутого обрыва на высоте над горизонтом, бросают небольшой
предмет в точку B горизонтальной поверхности, находящуюся от обрыва на расстоянии
. Чему равна
минимальная скорость броска? Под каким углом к горизонту должен при этом быть совершен бросок? С
какой скоростью предмет упадет на горизонтальную поверхность? Чему будет равен угол падения на
горизонтальную поверхность?
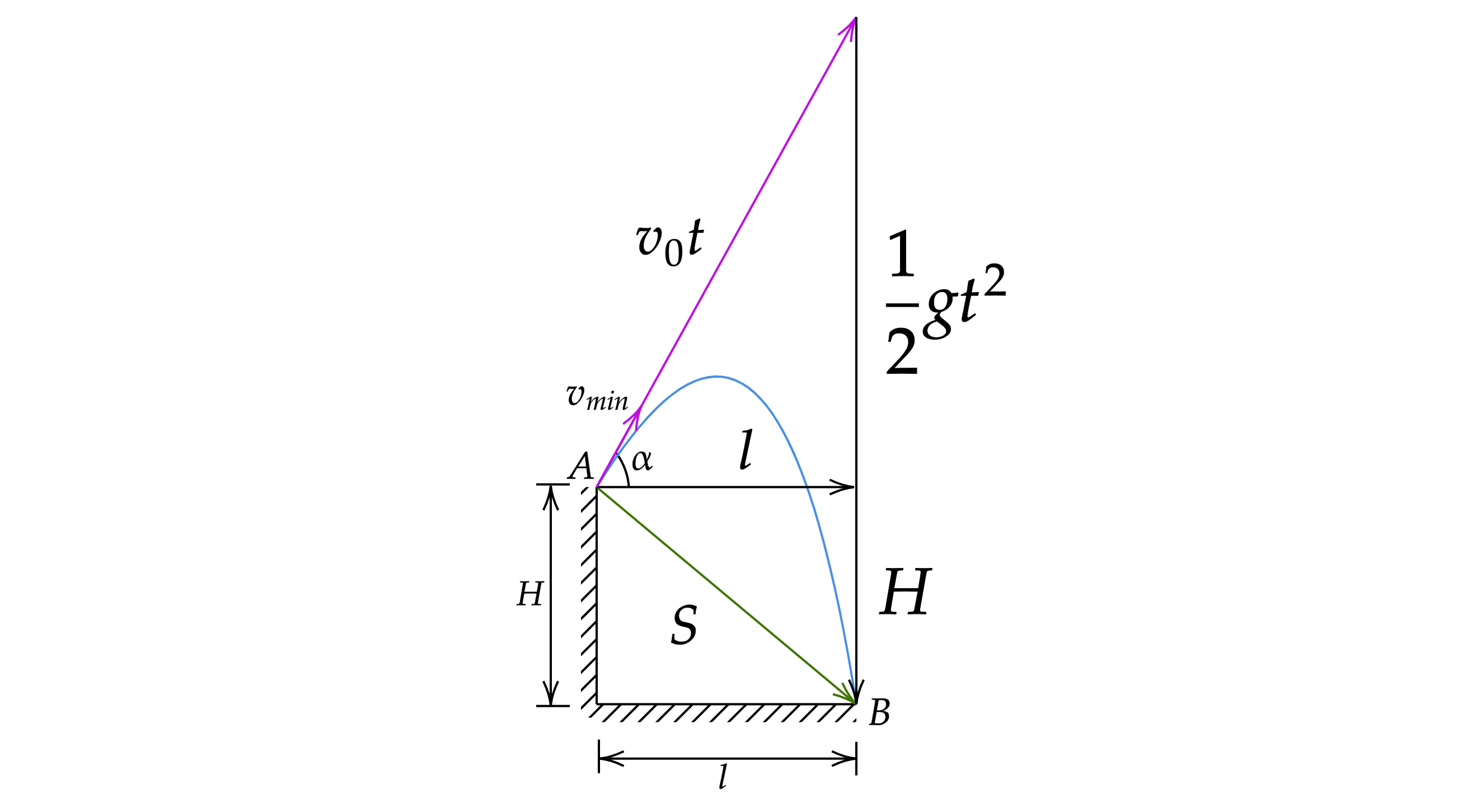
На рисунке - перемещение. Видим, что
Исключим из этих уравнение время, получим квадратное уравнение относительно
Анализ данного уравнение показывает, что при данном полете может реализовываться сразу несколько
ситуация:
1) слишком малое, чтобы долететь до точки В при любом из возможных углов;
2) При дискриминанте =
существует лишь один угол, при котором для заданной скорости
возможно попадание в В;
3) Существует скорость >
, при которой так же возможно попадание в В.
Ясно, что для соблюдения условия задачи необходимо, чтобы дискриминант =
(эквивалентно
при горизонтальном полете), тогда
А угол бросания выражается через тангенс как
Если положить, что =
, то
Теперь определим угол падения. Сделаем это, исходя из закона сохранения энергии. Вначале у тела была как кинетическая, так и потенциальная энергия, а в конце вся она перешла в кинетическую, тогда квадрат конечной скорсти
Таким же образом, как и с углом бросания, используя тригонометрию, определим тангенс угла
падения, из обратимости баллистики :
Не повторяя всех тригонометрических подсчетов, запишем
| Критерии оценивания выполнения задачи | Баллы |
| Использованы формулы кинематики равноускоренного движения | 2 |
| Найдена минимальная скорость бруска | 2 |
| Найден угол броска | 2 |
| Найдена скорость при падении | 2 |
| Найден угол, под которым упадет тело | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




