.07 Равноускоренное движение. Векторный подход - Красота
Ошибка.
Попробуйте повторить позже
Какова наибольшая длина простреливаемой области при стрельбе из-за вертикальной стенки
высотой
с начальной скоростью
? Под каким углом к горизонту следует осуществить
выстрел?
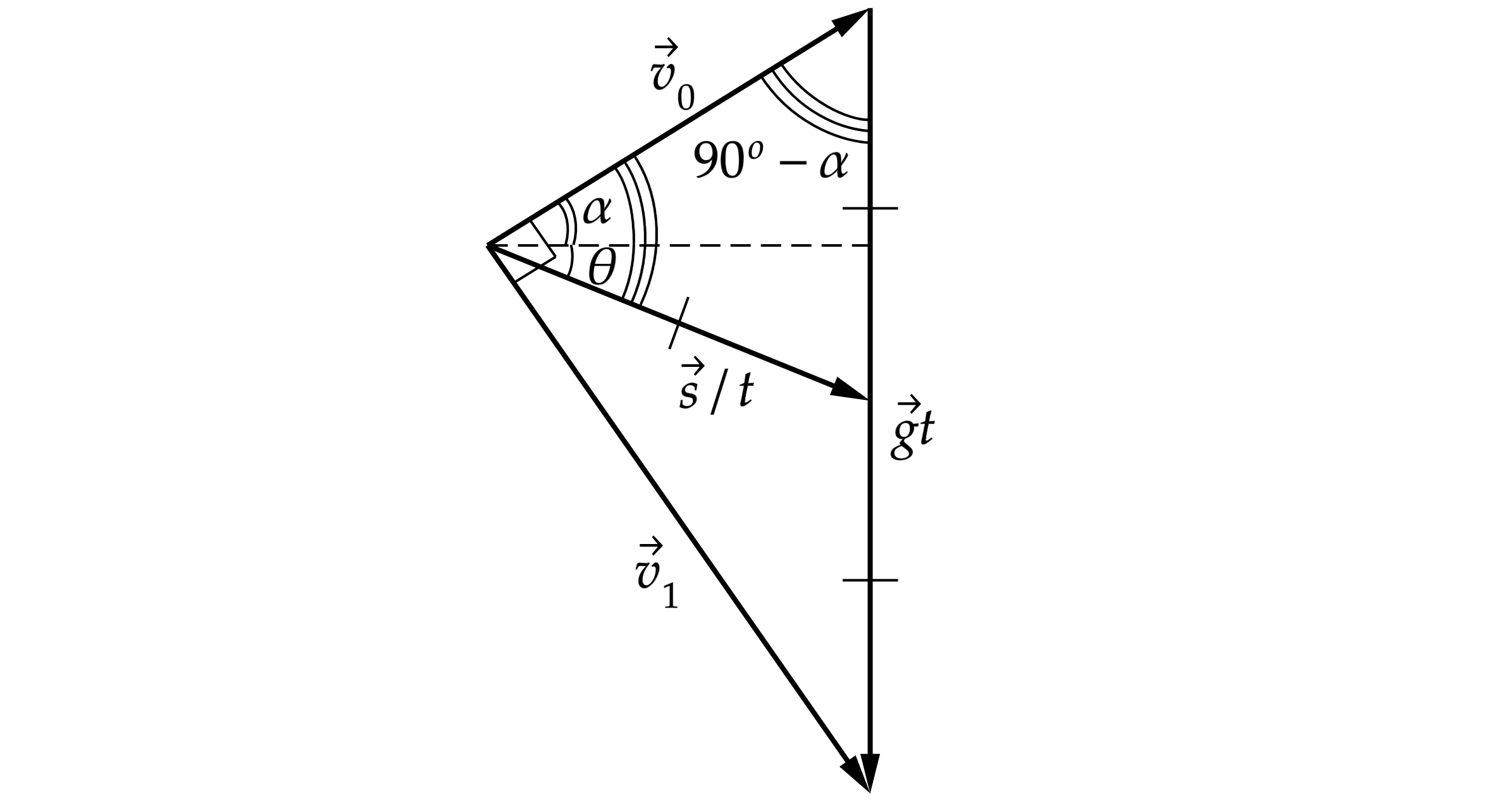
Рассмотрим бросок из-за стенки, чтобы длина простреливаемой области была максимальна, траектория броска должна проходить через вершину стенки. Запишем закон сохранения энергии для участка полета от точки броска до вершины стенки:
где – скорость в вершине стенки. Отсюда:
Пусть скорость направлена под углом
к горизонту. Дальнейший полет аналогичен броску с
вершины стенки со скоростью
под углом
к горизонту. В треугольнике скоростей площадь равна
, т.к.
– высота, а
– сторона, на которую она опущена. С другой стороны площадь равна
, где
– угол между скоростями, а
, поскольку изначальная скорость
броска равна конечной скорости. Отсюда получим выражение для длины простреливаемой
области:
Видно, что дальность максимальна при , т.е. скорости должны быть перпендикулярны.
Тогда из треугольника скоростей можем найти угол
:
Максимальная длина простреливаемой области равна:
| Критерии оценивания выполнения задачи | Баллы |
| Использован закон сохранения энергии | 2 |
| Получено выражение для скорости в вершине стенки | 2 |
| Получено промежуточное выражение для искомой длины | 2 |
| Получены необходимые тригонометрические соотношения | 2 |
| Получено итоговое выражение для искомой длины | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




