.07 Равноускоренное движение. Векторный подход - Красота
Ошибка.
Попробуйте повторить позже
Кот Леопольд стоял у края крыши сарая. Два злобных мышонка выстрелили в него из рогатки. Однако
камень, описав дугу, через упруго отразился от наклонного ската крыши сарая у самых лап
кота и через
попал в лапу стрелявшего мышонка (см. рисунок). На каком расстоянии
от
мышей находился кот Леопольд?
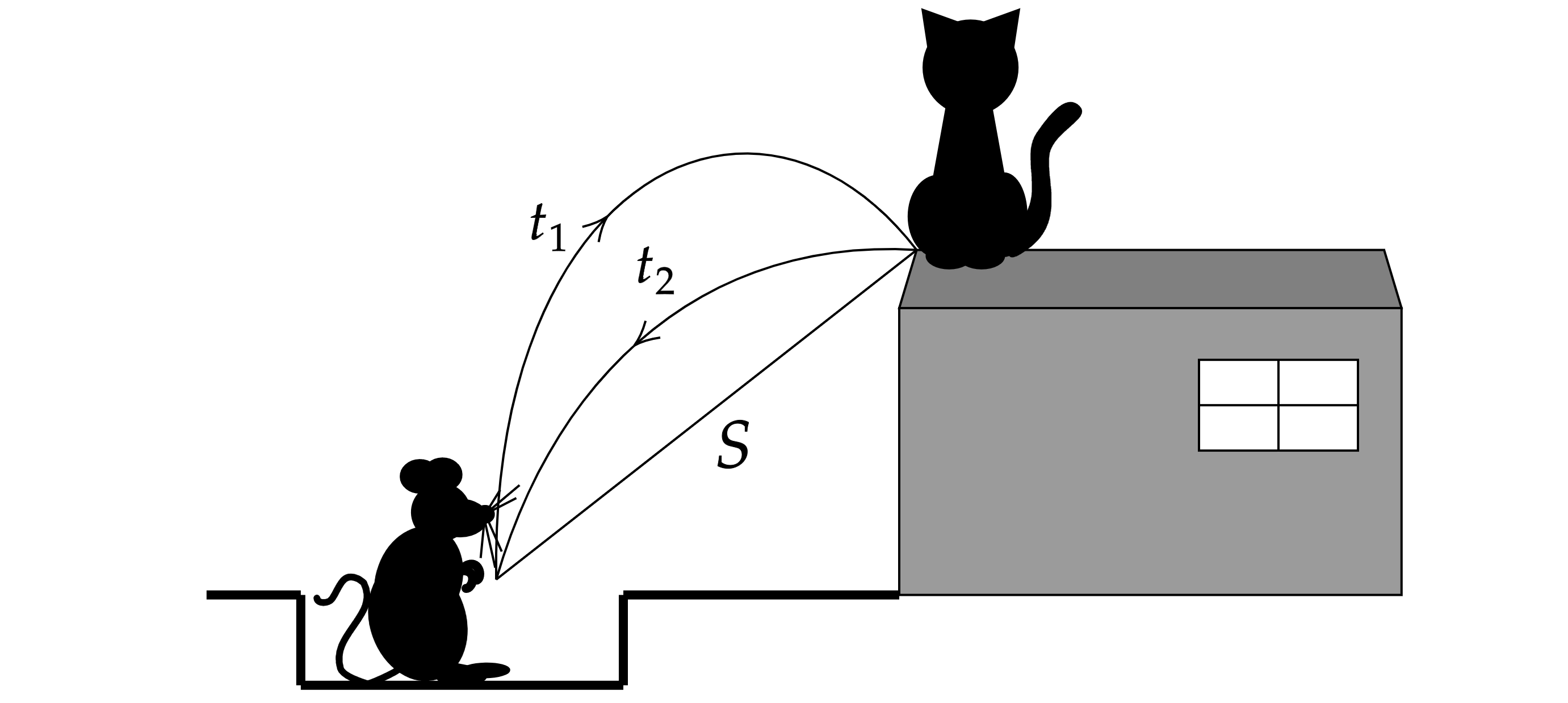
Изобразим полет камня к Леопольду и обратно
.png)
Нарисуем треугольники скоростей для полетов туда и обратно
.png)
.png)
Камень упруго отразился, следовательно, конечная скорость первого участка равна начальной
скорости для второго участка . С другой стороны поскольку обратно камень летит в точку
броска изменение потенциальной энергии такое же как при броске туда. Потерь кинетической энергии
при полете нет, значит кинетическая энегрии в конечной точкетакая же, как при броске из точки старта.
Отсюда
. Рассмотрим треугольники
и
. Площадь треугольника скоростей
пропорциональна
(высота
, сторона
), поскольку дальности при броске туда и обратно
равны, то равны и площади соответствующих треугольников скоростей. Медиана в треугольнике делит
его на два равновеликих, учитвая, что площади треугольников скоростей равны, то равны и площади
треугольников
,
,
,
. Теперь рассмотрим треугольники
и
. Они
имеют равны стороны(
), равные углы(векторы перемещений туда и обратно параллельны и
составляют равные углы с вертикалью) и равные площади, а значит и равные высоты. Такие
треугольники явлются равными(можно доказать при помощи "рельс Евклида"), значит
,
откуда получаем:
| Критерии оценивания выполнения задачи | Баллы |
| Верно записан закон движения мяча | 2 |
| Сказано про равенство скоростей после абсолютно упругого удара | 2 |
| Записано равенство скоростей | 2 |
| Нарисованы треугольники скоростей | 2 |
| Получены верные выражения для | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




