.02 Газовые законы
Ошибка.
Попробуйте повторить позже
Со дна глубокого озера всплывает пузырёк воздуха. На него действует сила сопротивления ,
где
— радиус пузырька,
— его скорость,
— постоянная. Вблизи дна радиус пузырька
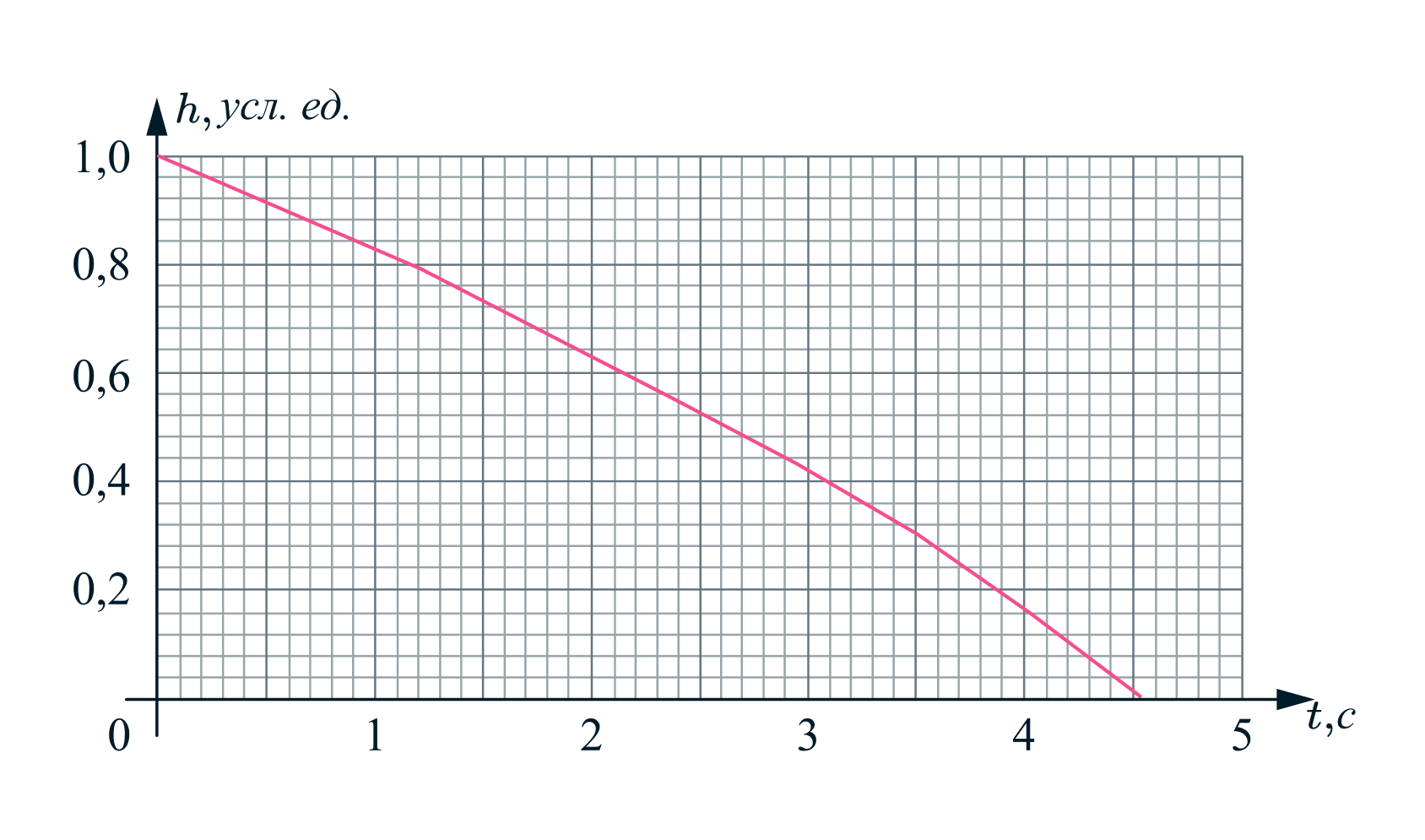
. На рисунке представлен график зависимости глубины
, на которой находится пузырёк,
от времени
, прошедшего от начала его движения.
1) Какова глубина озера?
2) За какое время всплывёт пузырёк, радиус которого у дна водоёма равен
?
3) За какое время пузырёк, радиус которого у дна водоёма равен
, всплывёт со дна
водоёма глубиной
?
Примечание. Давление водяных паров в пузырьке, поверхностное натяжение воды, изменение формы
пузырька и изменение температуры воздуха.
Источники:
Массу пузырька воздуха можно не учитывать, поэтому сила сопротивления движению равна силе
Архимеда
, или иначе:
. Отсюда найдём
. В соответствии с
законом Бойля-Мариотта
запишем:
Зависимость радиуса пузырька от глубины такова:
Откуда
Скорости пузырька вблизи дна и у поверхности
относятся как
Отношение скоростей можно определить через отношение угловых коэффициентов касательных,
проведенных к графику зависимости в соответствующих точках. Для нашего графика (данного в
условии)
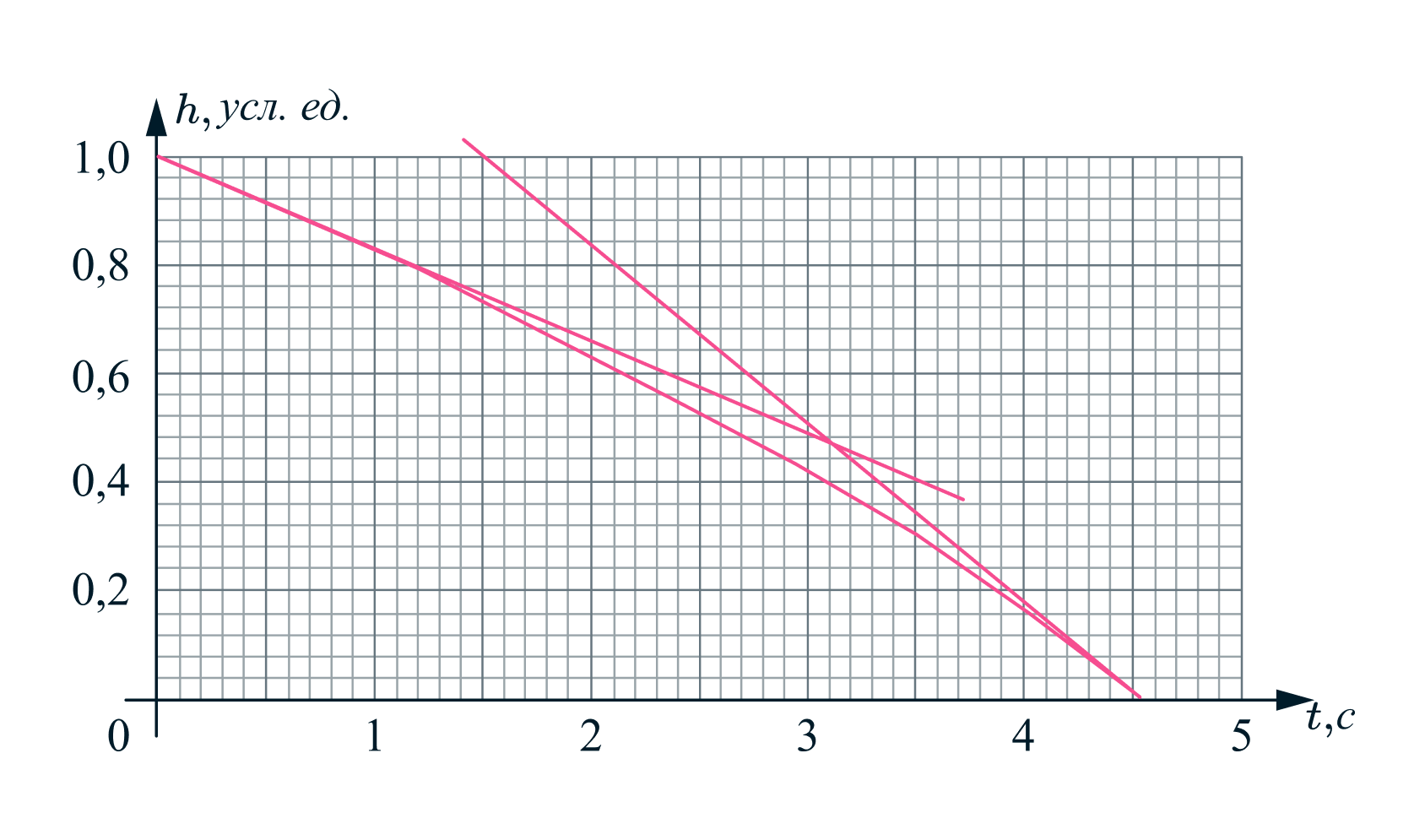
Для ответа на второй вопрос задачи достаточно заметить, что на любой глубине скорость пузырька,
пропорциональна квадрату его начального радиуса. Соответственно, для пузырька с начальным
радиусом скорость будет в четыре раза меньше, чем для пузырька радиусом
, а
время движения будет в четыре раза больше, то есть примерно
. При ответе на третий вопрос
задачи найдем радиус пузырька, имевшего
на глубине
, когда он достигнет глубины
.
Такой же пузырек в соответствие с графиком движется от глубины до поверхности
.
Пузырек, имеющий на этой глубине радиус
будет двигаться в
раз медленнее, то есть
достигнет поверхности за время
(Официальное решение ВсОШ)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




