.05 Изопроцессы
Ошибка.
Попробуйте повторить позже
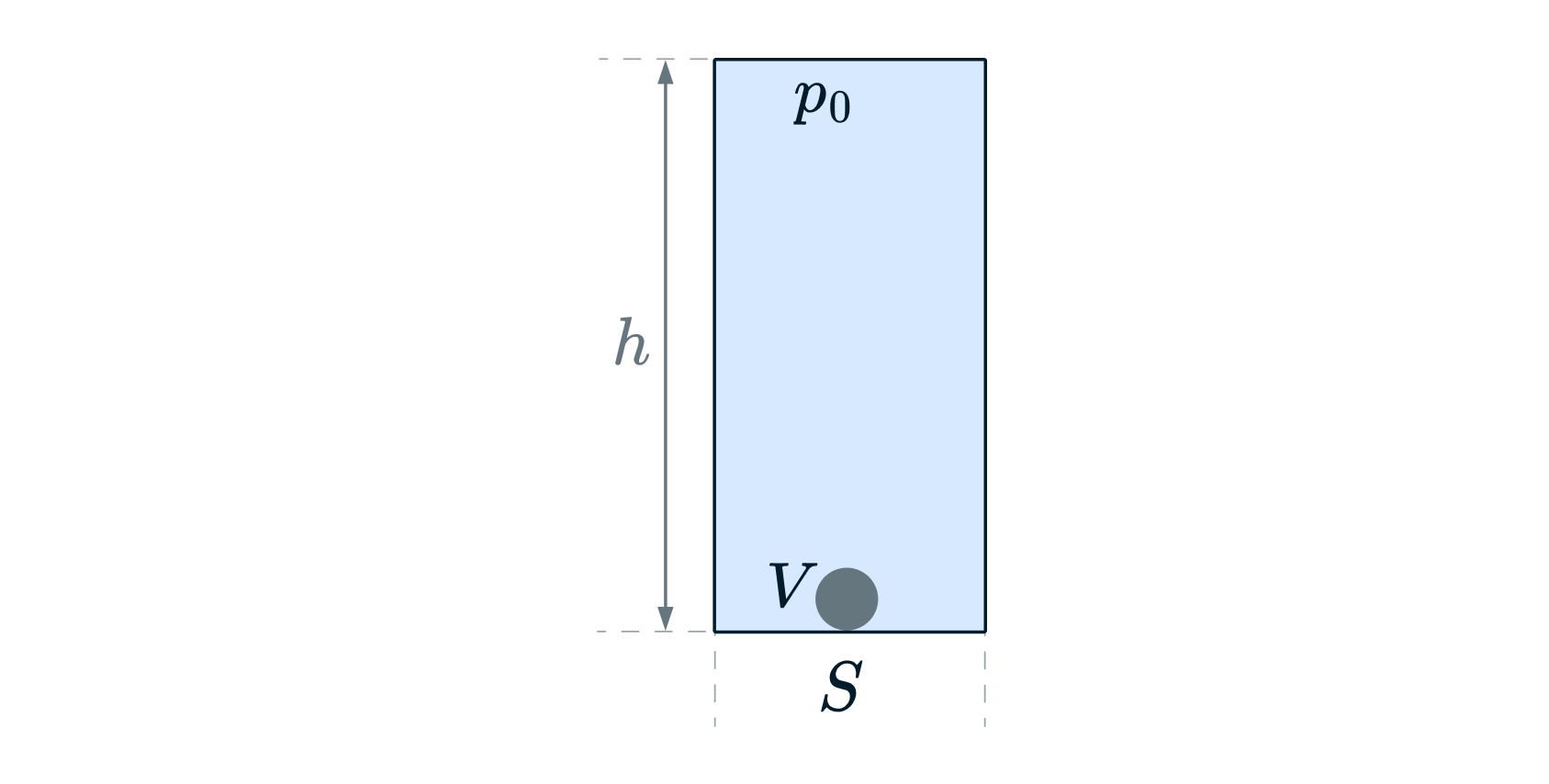
В высоком закрытом вертикально расположенном цилиндрическом сосуде сечением и высотой
находится вода, занимающая весь объём сосуда, кроме маленького пузырька воздуха объёмом
,
образовавшегося у дна (рис.). Давление воды в верхней части сосуда равно атмосферному давлению
.
Определите, каким будет давление воды в верхней части сосуда после того, как пузырёк поднимется
вверх. Процесс считать изотермическим. Модуль всестороннего сжатия жидкости равен
.
Рассмотрите предельные переходы:
1) ,
2) (сильно сжимаемая жидкость),
3) (несжимаемая жидкость).
Найдите численное решение задачи для случая ,
,
,
,
плотность воды
,
. Примечание. Модуль всестороннего сжатия жидкости
определяется соотношением
где — изменение давления,
— относительное изменение объёма жидкости.
Источники:
Давление воздуха в пузырьке у дна сосуда . Пусть после подъёма пузырька вверх
давление воздуха стало равным
, а объём
.
Поскольку , то
.
Так как процесс изотермический, . Обозначая отношение
через
, получим:
Решая квадратное уравнение, получаем:
Давление в верхней части сосуда
(Мы учли, что объём пузырька не может стать меньше нуля, и поэтому одно из решений не
подходит.) Числовой расчёт даёт для значение
Па.
Таким образом, при подъёме пузырька давление во всём сосуде возрастёт на величину
Па. При этом давление в пузырьке изменится на
Па. Следовательно,
. В предельных случаях расчёт даёт следующие результаты:
1. Из следует
.
2. Из следует
.
3. Из следует
.
Примечание. Так как относительное изменение давления в пузырьке при его подъёме достаточно мало,
можно было воспользоваться приближённой формулой, связывающей изменения давления и объёма
воздуха в пузырьке при его подъёме: . Из этой формулы следует
.
Формула для
приобретает следующий приближённый вид:
Предельные переходы дают те же результаты, что и при точном решении. Приближённое решение
будет рассматриваться как полное решение задачи при условии обоснованности его примени мости
.
(Официальное решение ВсОШ)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




