.03 Газовые процессы в трубках

Налетающие на пластину молекулы воздуха имеют среднеквадратичную скорость, равную

где – температура воздуха, – масса молекулы.
Среднее значение абсолютных величин проекций скоростей молекул на ось Oy, перпендикулярную к поверхности пластины, равно

При столкновении с пластиной "температура"молекул становится равной температуре пластины. Это означает, что после отражения от нижней поверхности пластины

А после отражения от верхней поверхности

В результате проекция импульса молекулы, попадающей на нижнюю поверхность пластины, меняется при соударении на величину

А молекулы, попадающей на верхнюю поверхность, - на величину

За время на каждую из поверхностей попадают молекулы, находящиеся от пластины на расстоянии, равном . Число этих молекул равно

где – число молекул в единице объема, – площадь пластины.

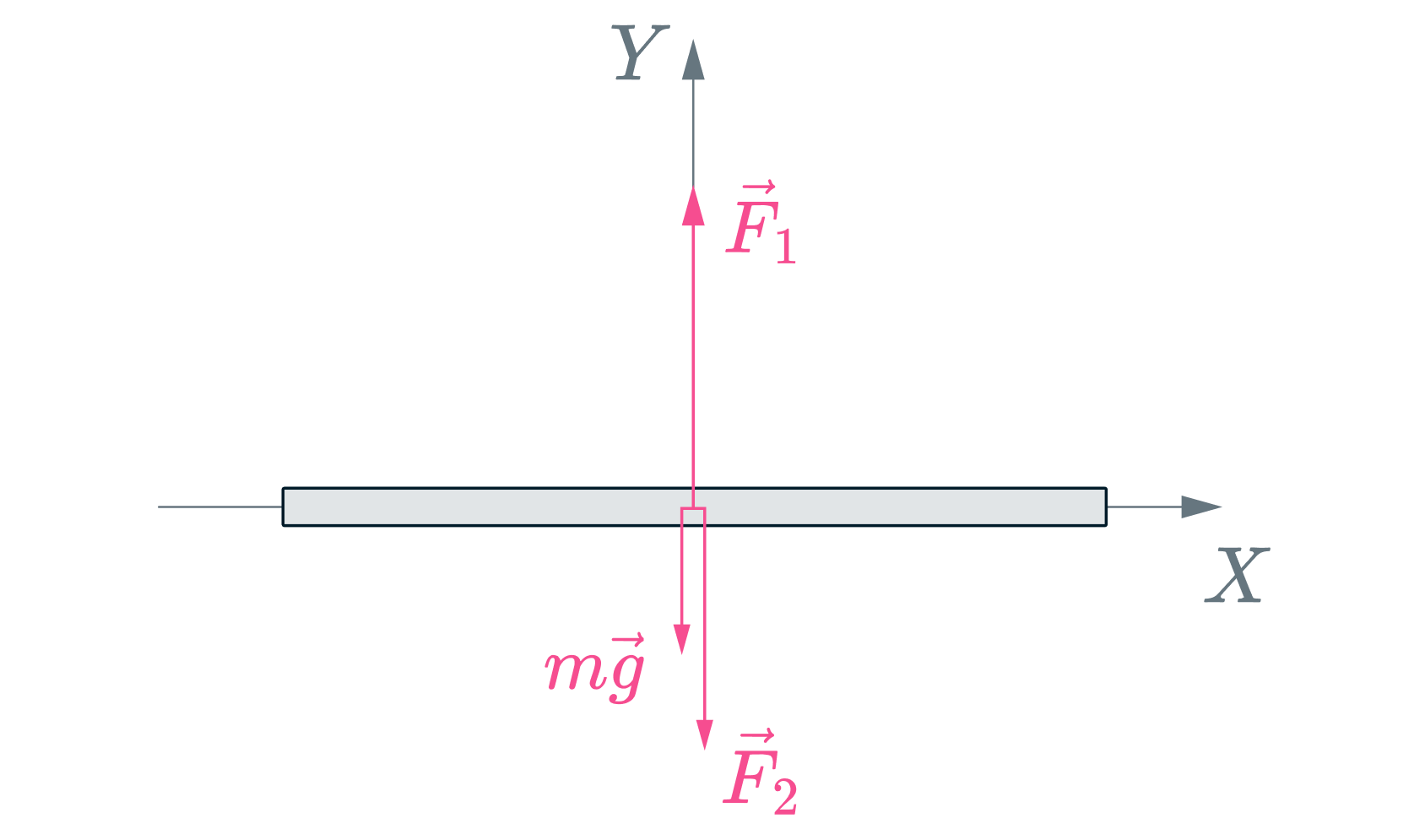
В соответствии со вторым и третьим законами Ньютона на пластину в вертикальном направлении действуют силы, равные по абсолютным величинам изменениям проекций импульсов молекул в единицу времени. На нижнюю поверхность пластины действует направленная вверх сила (рис.)

А на верхнюю - направленная вниз сила

Так как , то равнодействующая сил и направлена вверх и равна по абсолютной величине

Число молекул, содержащихся в объеме воздуха при давлении и температуре , равно

где – число молей воздуха в объеме , – число Авогадро.
Но

Так что число молекул в единице объема

Таким образом,