.01 Термодинамика процесса
Ошибка.
Попробуйте повторить позже
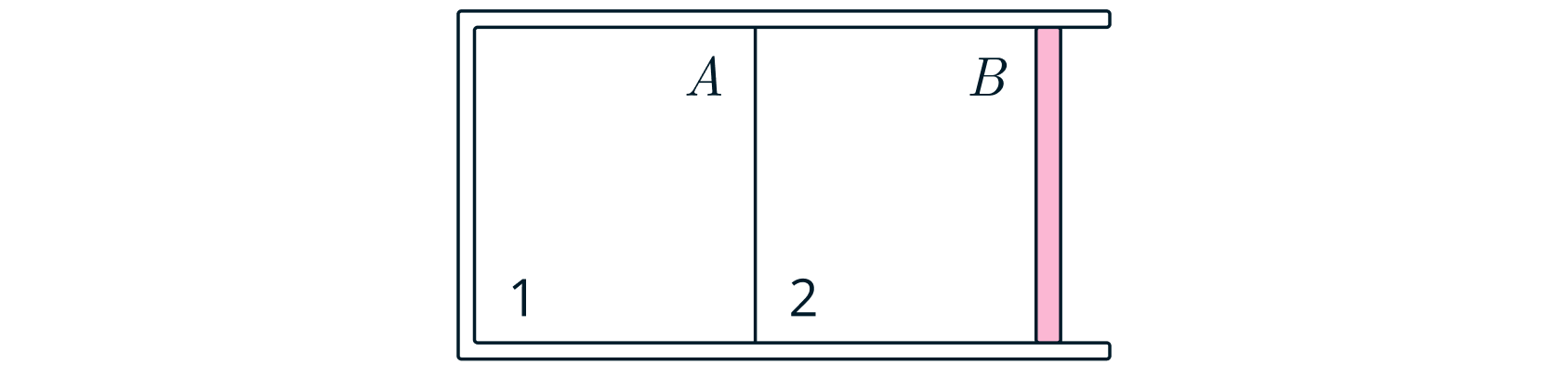
Неподвижная теплопроводящая перегородка делит объём теплоизолированного цилиндра на два отсека, в которых
находится по
моль гелия.
Во втором отсеке газ удерживается подвижным теплоизолированным поршнем Наружное атмосферное давление
равно
В начальном состоянии температура гелия в первом отсеке больше, чем во втором. В результате медленного
процесса теплообмена через перегородку температура в отсеках начинает выравниваться, а поршень перемещается. По
окончании процесса теплообмена объём гелия во втором отсеке увеличивается на
Трением поршня о цилиндр,
теплоёмкостью стенок цилиндра и поршня пренебречь.
1) Найдите отношение модулей изменения температуры в первом и втором отсеках после окончания теплообмена.
2) Найдите изменение температуры в первом отсеке.
(«Физтех», 2015, 11)
Источники:
1. В левой части сосуда происходит изохорный процесс () (т. к. перегородка неподвижна), в правой части
сосуда происходит изобарный процесс (
)
2. Поймем, как соотносятся и
в изобарном процессе:
В связи с этим:
3. Теперь нам известно, как соотносятся и
в изобарном процессе. Воспользуемся результатом первого пункта и
получим:
Тогда получаем ответ на первый вопрос задачи:
3. Для изобарного процесса:
Тогда воспользуемся ответом на первый пункт:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




