.01 Термодинамика процесса
Ошибка.
Попробуйте повторить позже
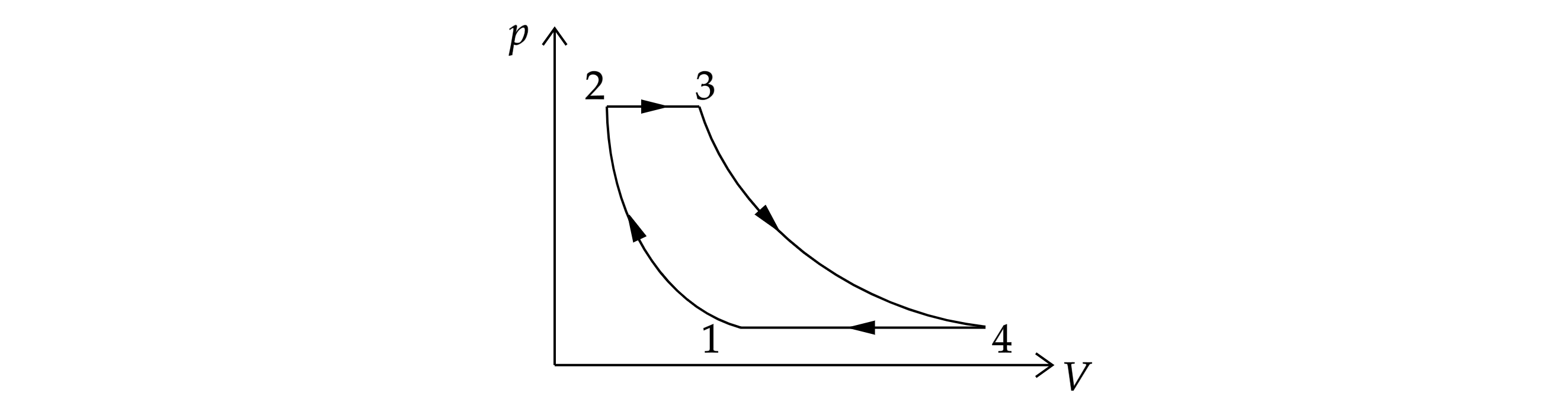
С идеальным газом проводят циклический процесс 1–2–3–4–1, состоящий из двух изотерм
(1–2 и 3–4) и двух изобар (2–3 и 4–1; см. рисунок). Известно, что отношение температур
на изотермах 1–2 и 3– 4 равно , а на участке изотермического расширения газ
получал в 3 раза больше тепла, чем на участке изобарического нагревания 2–3. Найти КПД
цикла.
Источники:
Пусть на участке изобарического нагревания 2-3 газ получил количество теплоты . Тогда на участке
изотермического расширения 3-4 газ получил количество теплоты
. И, следовательно, количество
теплоты, полученное от нагревателя, в течение цикла, равно
Найдем работу газа за цикл. Очевидно, работа газа на участке 2-3 и работа газа на участке 4-1 равны
по модулю. Действительно, работа газа в изобарическом процессе при давлении с изменением объема
равна
т.е. определяется только разностью начальной и конечной температур, которая в процессах 2-3 и 4-1
отличается только знаком. Поэтому работа газа за цикл равна Работу газа в этих
процессах найдем как площадь под графиком зависимости давление от объема. Очевидно, эти площади
отличаются в 2 раза. Действительно, из закона Клапейрона-Менделеева следует, что объем газа в
состоянии 3 в два раза больше объема в состоянии 2:
, а объем в состоянии 4 в два раза
больше объема в состоянии 1:
. Следовательно, изменение объема газа в процессе 3-4 в два раза
больше изменения объема газа в процессе 1-2:
Поэтому если разбить изменение объема
на малые элементы
, то изменение объема
можно разбить на такое же количество
элементов, каждый из которых вдвое больше соответствующего элемента
, а
давление газа в пределах соответствующих элементов одинаковое. В результате для работы газа
имеем
А поскольку процесс 3-4 изотермический, работа газа равна количеству теплоты, полученному в этом
процессе: Отсюда получаем
Поэтому КПД цикла
есть
(Официальное решение Росатом)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




