.03 Уравнение адиабаты. Политропические процессы. Теплоемкость газа
Ошибка.
Попробуйте повторить позже
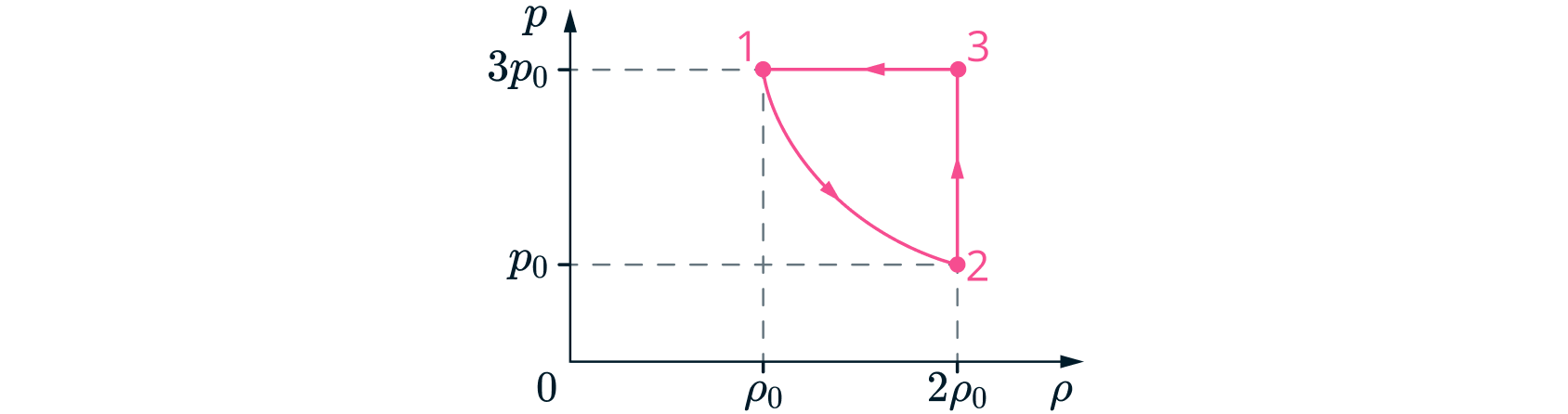
Циклический процесс, проводимый с одноатомным идеальным газом, представлен на графике в координатах ,
здесь
- давление,
- плотность газа. Количество вещества - один моль. В процессе 1-2 давление газа
изменяется по закону
, здесь
и
- постоянные. Максимальная внутренняя энергия газа в процессе
.
1. Постройте график процесса в координатах . В состоянии 1 объем газа
, давление газа
.
2. Найдите работу газа за цикл.
3. Какое количество теплоты будет отведено от газа в начале процесса сжатия при уменьшении температуры на
? Универсальная газовая постоянная
.
(«Физтех», 2025, 10)
Источники:
1. Выразим давления в состояниях и
через зависимость от плотности:
Отсюда можем выразить постоянные в этой зависимости:
Тогда можем выразить зависимость давления от объема в процессе :
Получаем линейную зависимость давления от объема. В процессе плотность постоянна, а значит и объем, т.е.
процесс изохорический. В процессе
давление постоянно, т.е. процесс изобарический. Построим цикл в координатах
:
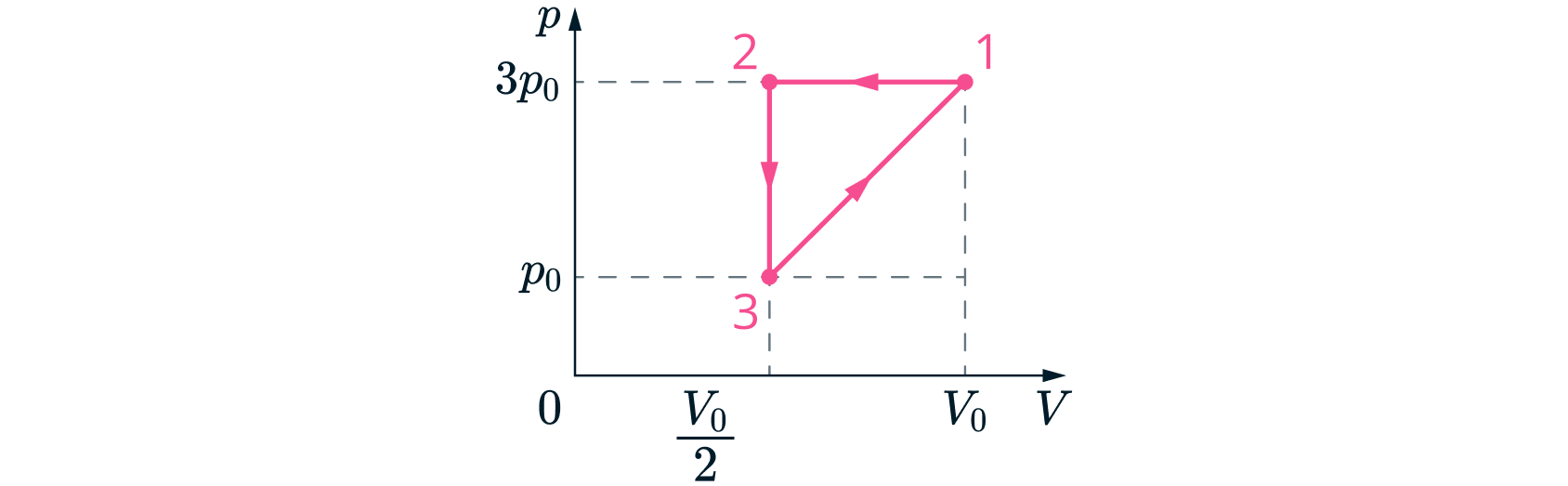
2. Работа газа за цикл:
Распишем максимальную внутреннюю энергию газа в процессе:
Тогда искомая работа:
3. Молярная теплоемкость газа в процессе по определению:
По первому началу термодинамики для малого количества тепла:
Для изменения внутренней энергии имеем:
где – молярная теплоемкость при постоянном объеме.
Объединяя уравнения, получим:
Запишем уравнение Менделеева-Клапейрона:
Возьмем малое приращение от него:
Поделив полученное уравнение на уравнение состояния, получим:
Подставим в формулу для теплоемкости:
В процессе сжатия:
В начале процесса сжатия:
Тогда:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




