.03 Уравнение адиабаты. Политропические процессы. Теплоемкость газа
Ошибка.
Попробуйте повторить позже
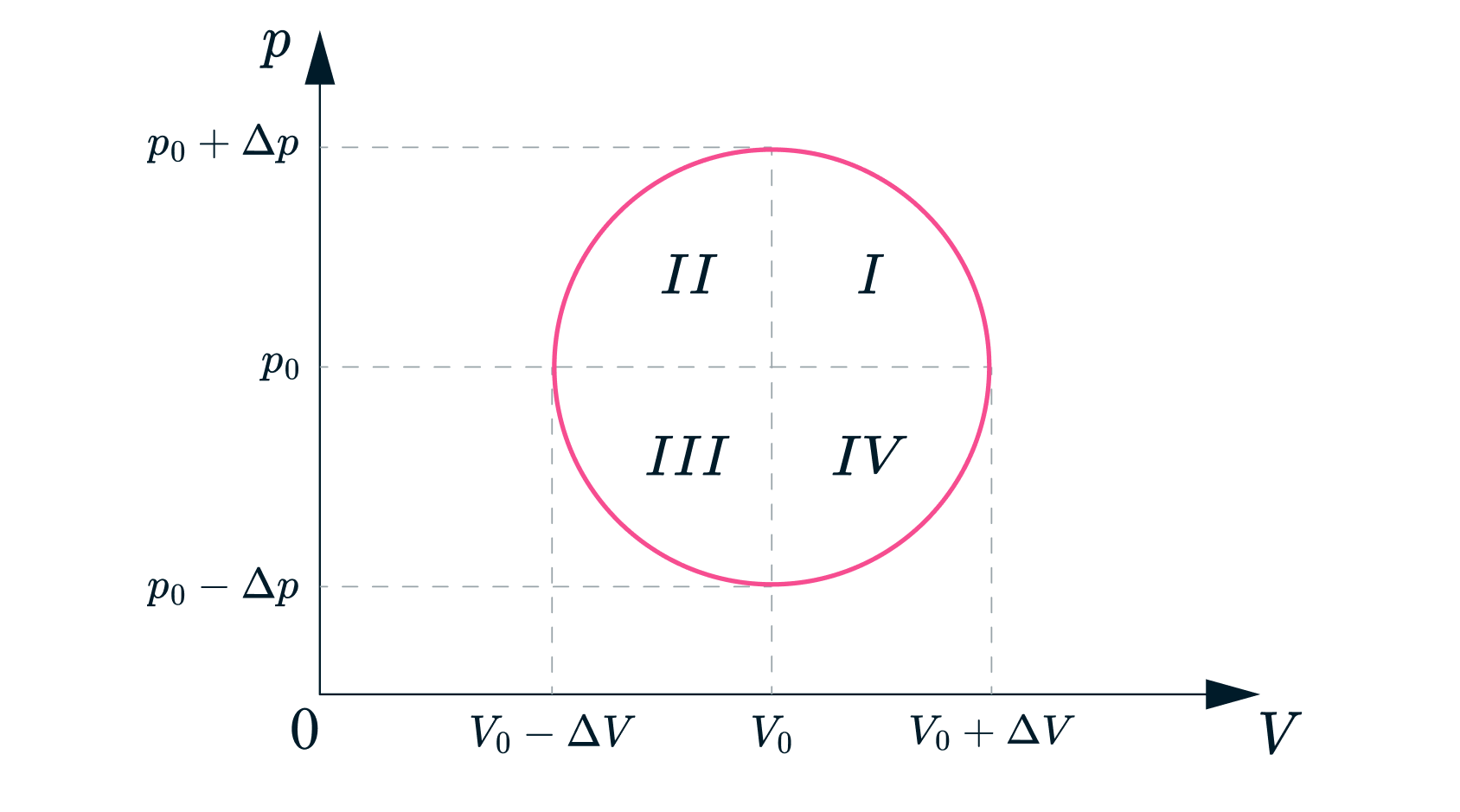
Над молем идеального многоатомного газа проводят круговой процесс, который, будучи изображённым
на
– диаграмме, при некотором масштабе имеет вид окружности. Центр окружности имеет
координаты (
,
), диаметр вдоль оси давлений равен
, а диаметр вдоль оси объёмов —
.
1) Найдите все пары диаметрально противоположных точек окружности, в которых теплоёмкости
одинаковы. Вычислите эти теплоёмкости.
2) Сравните теплоёмкости двух произвольных диаметрально противоположных точек, лежащих во 2 и 4
квадрантах окружности (см. рисунок); другими словами, определите, в какой из этих точек
теплоёмкость больше и почему.
Примечание. Считайте, что теплоёмкость газа при постоянном объёме не зависит от T.
(Всеросс., 2016, финал, 11 )
Рассмотрим моль идеального газа. По определению его теплоёмкость
Для идеального газа:
Выразим теплоёмкость:
В любых диаметрально противоположных точках A и B касательная к окружности имеет один и тот же наклон:
Значит, теплоёмкости могут быть равны либо когда обращается в ноль, либо бесконечность,
чему соответствует
и
соответственно, либо когда:
то есть когда точки A, B и центр окружности лежат на одной прямой, идущей из начала координат. Значит
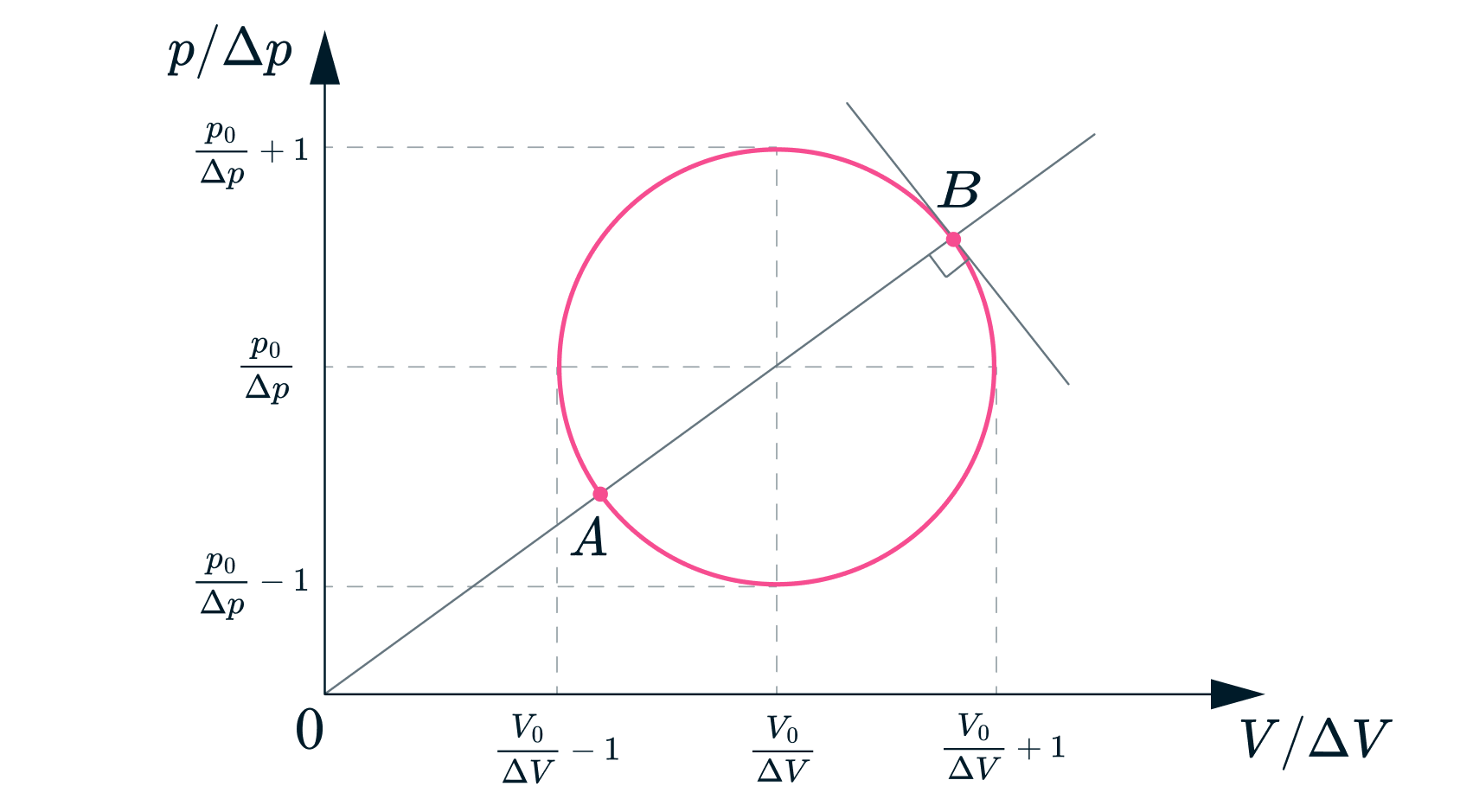
Перерисуем процесс в безразмерных осях координат (см. рис.). Проведём прямую через точки A и B.
Построим касательную к графику в точке B. Она будет перпендикулярна прямой AB. Таким образом,
если угловой коэффициент прямой AB равен k, то угловой коэффициент касательной будет равен
, следовательно:
Теплоёмкость равна:
Если , то
точки касания принадлежат изотермам.
Сравним теплоёмкость в точках C и D, лежащих во 2 и 4 квадрантах соответственно. Поскольку
то теплоёмкость больше там, где отношение меньше:
Получается, в нашем случае .
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




