.03 Уравнение адиабаты. Политропические процессы. Теплоемкость газа
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
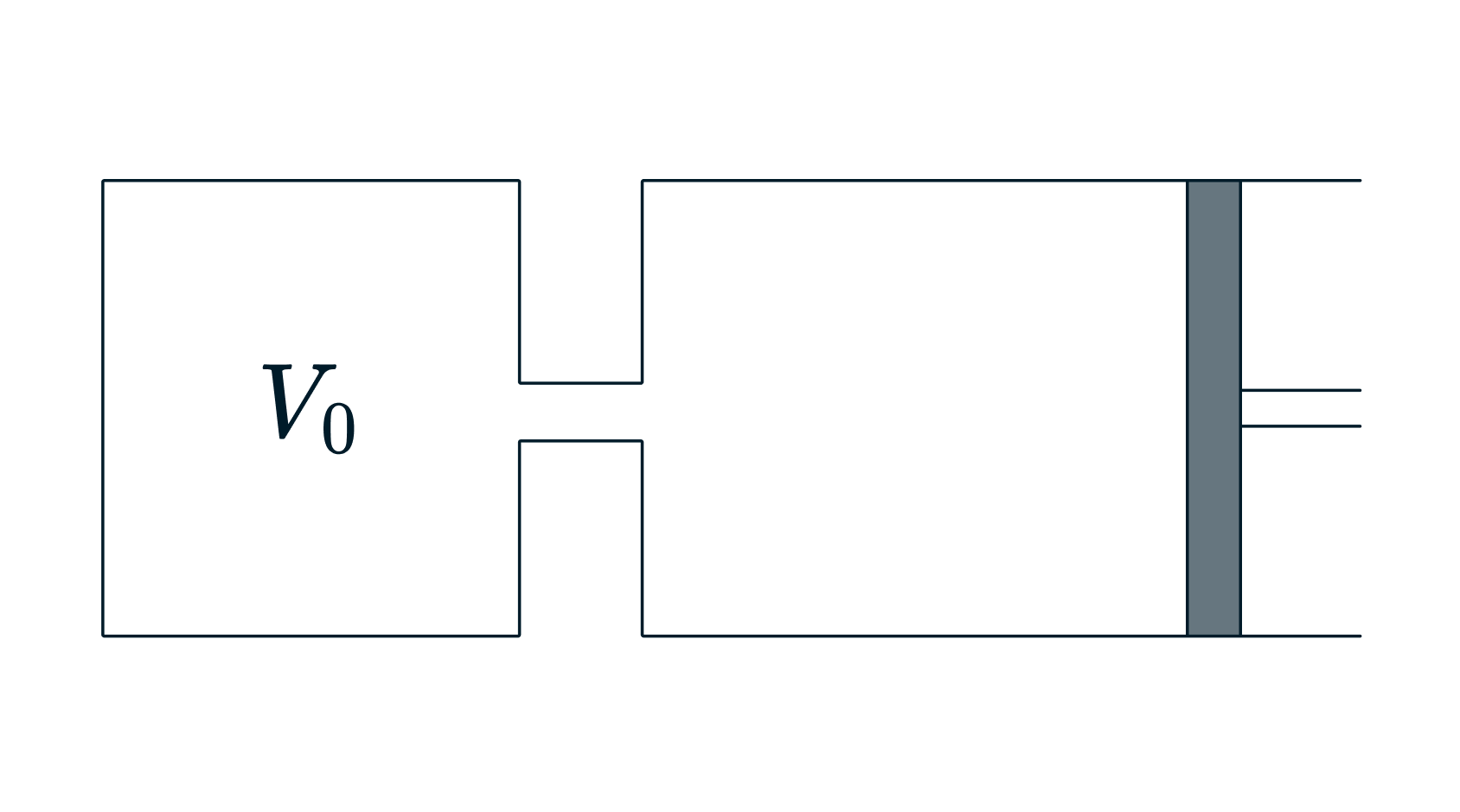
На рисунке изображена система, состоящая из баллона объёмом 
м
и цилиндра с
поршнем. Начальный объём баллона и цилиндра 
, где 
. В системе находится
воздух под давлением 
Па и при температуре 
К, равной температуре
наружного воздуха. Передвигая поршень, весь воздух из цилиндра закачивают в баллон.
Определите количество теплоты, которое передаётся окружающей среде в следующих двух
случаях.
1) Поршень передвигается медленно, так что в каждый момент времени вся система находится в
тепловом равновесии с окружающей средой.
2) Поршень передвигается достаточно быстро, так что за время его перемещения можно пренебречь
теплообменом с окружающей средой, но воздух внутри системы в каждый момент времени находится в
равновесном состоянии. После завершения процесса перекачки температура воздуха в баллоне
постепенно сравнивается с температурой окружающего воздуха. Примечание. Адиабатический процесс
описывается уравнением 
, где параметр 
.
(Всеросс., 2006, финал, 11 )
В обоих случаях конечная температура воздуха в баллоне равна 
, следовательно, его
внутренние энергии в начальном и конечном состоянии одинаковы. Поэтому окружающей
среде в каждом случае будет передано количество теплоты, равное работе внешних сил по
перемещению поршня. Начальное состояние: 
К, 
Па, 
м
,
. Конечное состояние: 
К, 
, 
м
. Показатель адиабаты
Первый случай (квазистатическое перемещение поршня): происходит изо термическое сжатие,
следовательно 
, откуда 
.. Поскольку внутренняя энергия не меняется, то по
первому закону термодинамики количество теплоты, полученное газом,
, или T 
. Из уравнения
адиабаты 
следует, что 
К. Работа газа при адиабатическом
сжатии
Дж
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
