Количество способов, исходов, слагаемых

Рассмотрим как могут выглядеть квадратики .

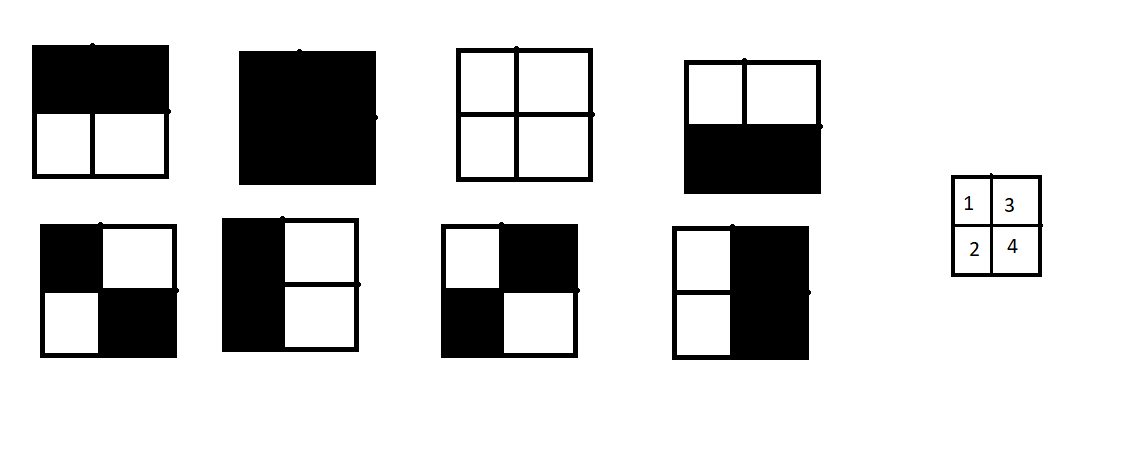
Заметим, что в каждом маленьком квадратике верхний и нижний ряд либо полностью совпадает, либо полностью противоположный. Хотелось бы доказать, что любые ряда в большой таблице либо полностью совпадают, либо полностью противоположные. Возьмем соседних ряда. Пусть они начинаются с одного цвета. Посмотрим какие могут быть вторые клетки в этих рядах. Заметим, что они так же должны быть одинаковыми, так как первые и вторые клетки двух соседних строк образуют квадрат . Аналогично и третьи клетки, и четвертые, и все последующие клетки в этих рядах будут совпадать. Значит, оба ряда будут совпадать. Если же первые клетки разных рядов будут разными, то тогда и вторые, и все последующие клетки будут разными.

Таким образом, мы доказали, что соседних ряда либо полностью совпадают, либо полностью противоположные. Посчитаем, сколько таблиц с таким свойством. Первую строку можно расставить как угодно и, значит, для нее вариантов, так как каждая клетка может быть или черной, или белой. Вторую строку придется заполнять либо как первую, либо полностью противоположно ей и, значит, для второй строки только варианта. Аналогично для строк с до и итого вариантов. Осталось доказать, что если выполнено наше свойство, то будет выполнено и условие задачи. Это так, потому что выше нарисовано как могут выглядеть все квадраты в таблице с таким свойством, и все они подходят под условие.