.05 Кинематические связи
Ошибка.
Попробуйте повторить позже
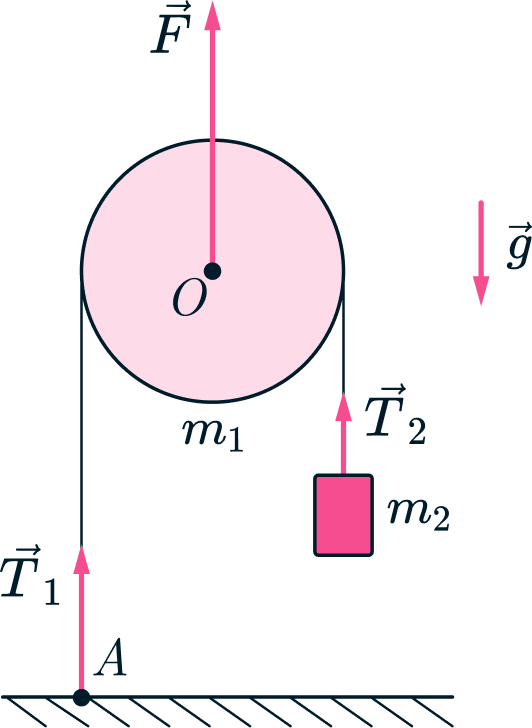
Блок, представляющий собой тонкий обруч с невесомыми спицами, может свободно вращаться вокруг горизонтальной оси,
проходящей через его центр . Масса обруча
равномерно распределена по его длине. Через блок
переброшена невесомая и нерастяжимая нить, к правому концу которой подвешен груз массой
. Левый
вертикальный участок нити закреплён на полу в точке
. Ось блока поднимают вверх, действуя на неё постоянной силой
. Ускорение свободного падения
. Считая, что при движении нить не скользит по блоку, найдите
следующие величины:
- Ускорения оси блока
и груза
.
- Отношение
, где
,
и
— силы натяжения левого и правого вертикальных участков нити. Числовое значение
округлите до сотых.
(Курчатов 2025, 11)
Пусть и
— мгновенные скорости оси блока и груза,
— мгновенное значение угловой скорости вращения блока
вокруг своей оси,
— радиус блока. Рассмотрим мгновенные скорости
и
точек блока
и
, лежащих
на концах его горизонтального диаметра. В точке
блок касается левого вертикального участка нити.
Так как нить нерастяжима, скорости всех точек этого участка равны скорости точки
, то есть нулю.
Поскольку нить не скользит по блоку, скорость
также обращается в нуль. В точке
блок касается
правого вертикального участка нити, скорости всех точек которого равны
. Поэтому
. Используя
закон сложения скоростей, находим связь скоростей
и
и, как следствие, связь ускорений
и
:
Отсюда получаем:

Рассмотрим полную механическую энергию системы, состоящей из блока, нити и груза. Для того чтобы правильно
записать кинетическую энергию блока, воспользуемся известным фактом, что если тонкий обруч массой
катится без
проскальзывания по столу, то его кинетическая энергия равна
, где
— скорость центра обруча. В
нашем случае роль стола играет левый вертикальный участок нити
. Блок как бы катится вверх по
этому неподвижному участку. Отсутствие проскальзывания соответствует обращению в нуль скорости
.
Таким образом, в нашей задаче кинетическая энергия обруча равна
. Учитывая равенство
,
получаем:
где и
— высоты оси обруча и центра масс груза над полом.
Рассмотрим баланс энергии системы за малое время :
Здесь в левой части стоит приращение энергии , в правой части — работа силы
на перемещении
. В
связи с этим равенством следует отметить два обстоятельства:
- Сила, действующая на нить со стороны пола в точке
, не совершает работу, поскольку скорость точки
равна нулю.
- Так как нить не скользит по блоку, силы трения, действующие между блоком и верхним участком нити, являются силами трения покоя. Суммарная работа этих сил равна нулю (другими словами, при взаимодействии нити с блоком не выделяется тепло).
Запишем приращение энергии :
Обозначим через приращение скорости оси блока за время
. Тогда для приращения квадрата скорости
имеем:
При уменьшении отношение
становится сколь угодно малым и может быть отброшено.
Тогда:
Приращения высот и
равны:
Собирая всё вместе, получаем:
Введём ускорение оси блока :
Тогда и выражение для
принимает вид:
Подставляя этот результат в уравнение баланса энергии, находим ускорение :
Ускорение груза в два раза больше:
Для того чтобы найти силы натяжения и
, запишем второй закон Ньютона для системы, состоящей из блока и
верхнего участка нити. Внешними силами, действующими на эту систему, являются сила
, сила тяжести
и
направленные вниз силы натяжения, действующие со стороны вертикальных участков нити. Так как нить невесома, эти
силы равны
и
. Получаем:
Запишем также второй закон Ньютона для груза:
Используя полученное выше выражение для ускорения и равенство
, после некоторых алгебраических
преобразований находим силы натяжения и их разность:
Отношение равно:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




