.05 Кинематические связи
Ошибка.
Попробуйте повторить позже
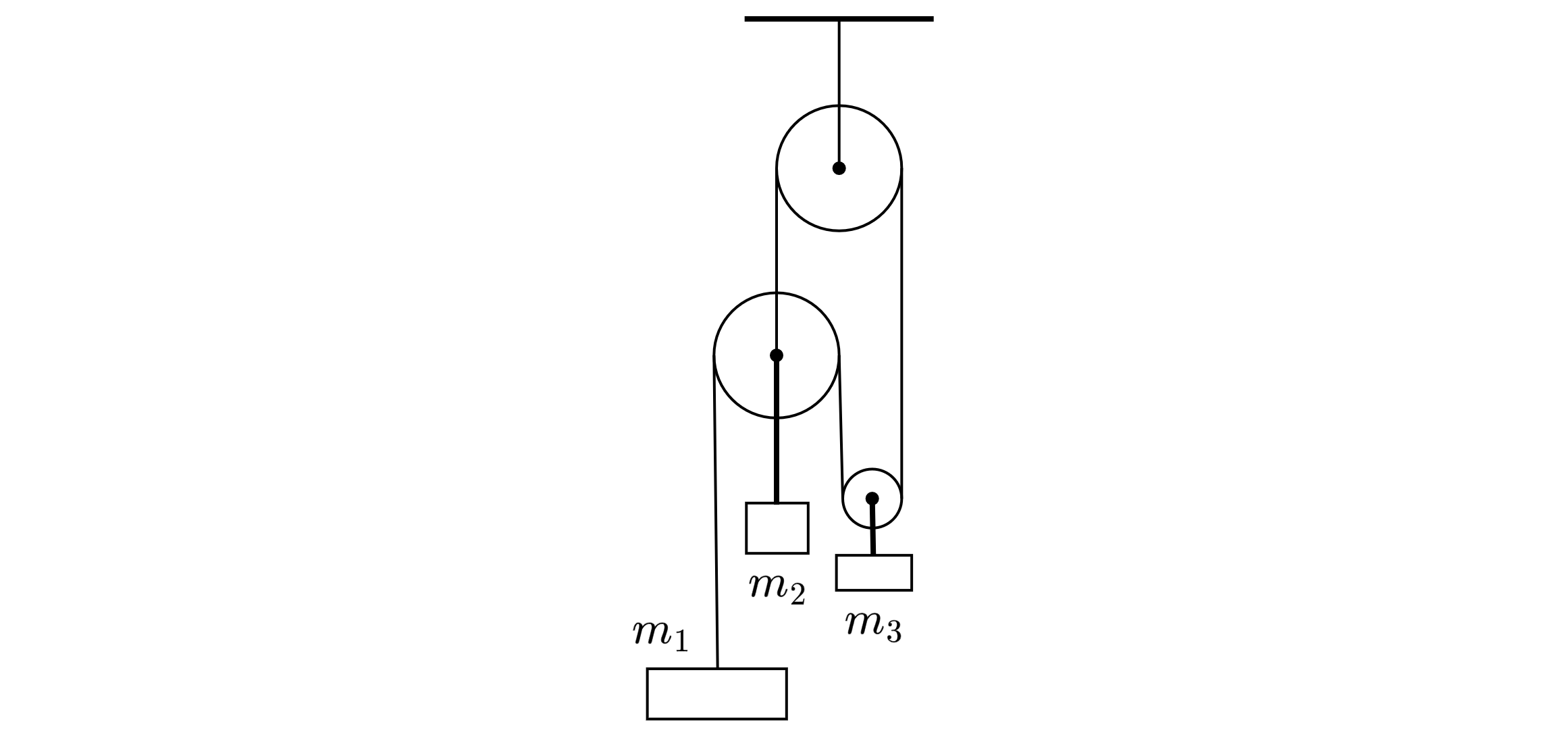
В системе, показанной на рисунке, неподвижный блок прикреплён к потолку комнаты, а все грузы удерживают
неподвижными так, чтобы отрезки лёгкой нерастяжимой нити, не лежащие на блоках, были вертикальны. Грузы массами
и
подвешены к осям блоков на жёстких лёгких стержнях. Все блоки лёгкие и могут вращаться вокруг своих осей
без трения. Определите ускорение груза массой
после одновременного отпускания всех грузов. Ускорение свободного
падения равно
.
(МОШ, 2009, 9)
Источники:

Запишем Второй закон Ньютона на вертикальную ось для грузов:
Уравнение кинематических связей, связанное с нерастяжимостью нити:
где - длина нитей на блоках, причем
.
Т.к.
Путем дифференцирования получаем
В итоге получаем
Тогда
| Критерии оценивания выполнения задачи | Баллы |
| Верно записана система уравнений Ньютона для грузов | 2 |
| Записано уравнение кинематической связи, следующей из нерастяжимости нити | 2 |
| Получена связь ускорений | 2 |
| Выражена сила натяжения нити | 2 |
| Представлен правильный ответ | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




