.05 Кинематические связи
Ошибка.
Попробуйте повторить позже
Изображённая на рисунке система состоит из грузов массами и
, двух неподвижных и одного подвижного блока.
Не лежащие на блоках участки нитей вертикальны. Определите ускорения грузов, считая, что груз массой
при
движении сохраняет горизонтальное положение, нити невесомы и нерастяжимы, блоки лёгкие, трения нет.
(МОШ, 2012, 9 )

Источники:
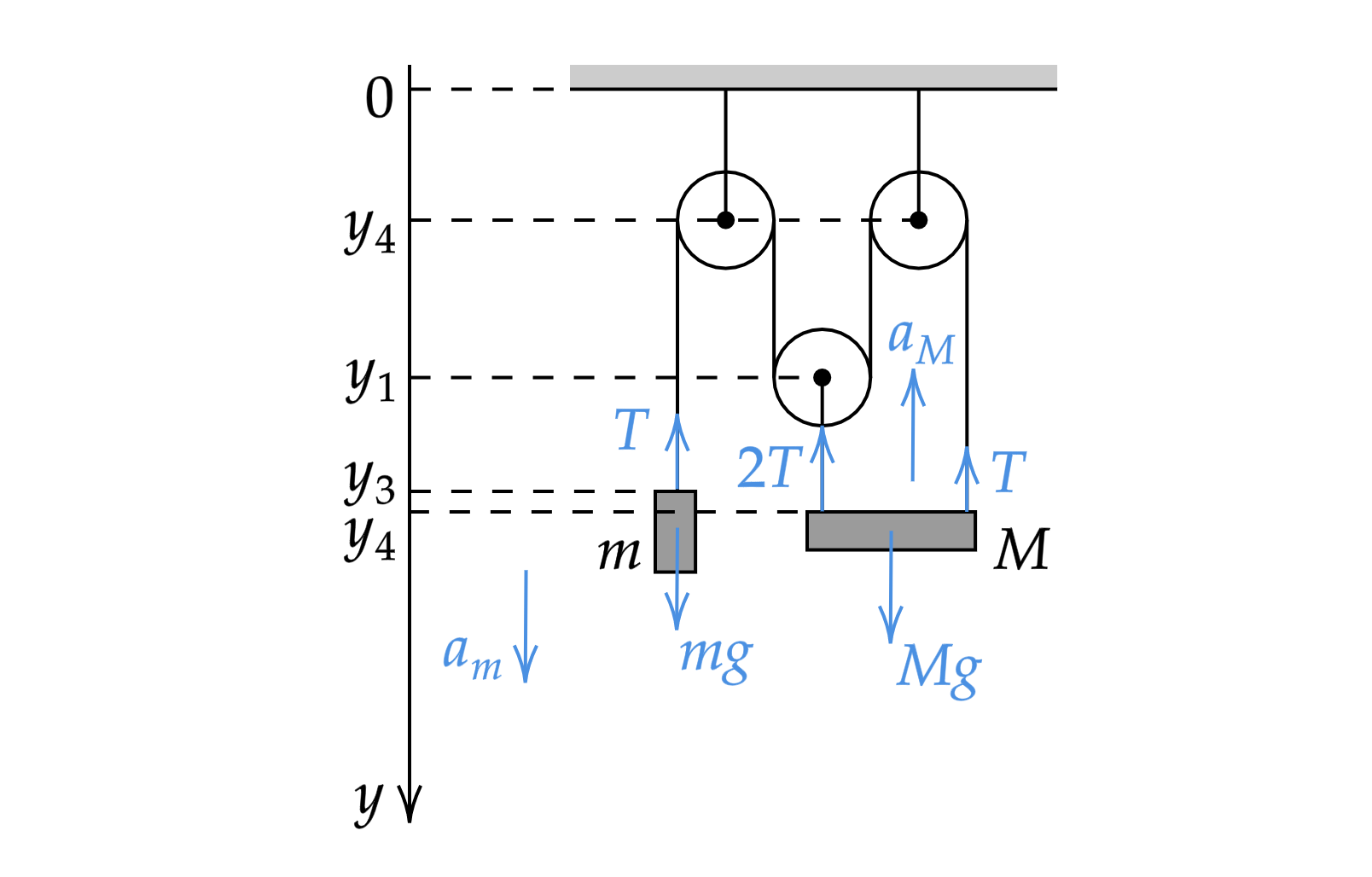
Найдем длину нити
Продифференцируем
Так как груз массой сохраняет горизонтальное положение, то
. Откуда
Опять дифференцируем
Перейдем от проекций к модулям
Запишем второй закон Ньютона
|
|
Складываем
А ускорение груза массой направлено противоположно и равно
| Критерии оценивания выполнения задачи | Баллы |
| Записана связь перемещений грузов (отличаются по величине в три раза, направлены противоположно) | 2 |
| Записана связь ускорений грузов (отличаются по величине в три раза, направлены противоположно) | 2 |
| Записан второй закон Ньютона для груза массой | 2 |
| Записан второй закон Ньютона для груза массой | 2 |
| Получены правильные ответы для ускорений грузов массой | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




