Геометрическая прогрессия
Ошибка.
Попробуйте повторить позже
Первооткрыватель летел над джунглями на вертолёте и заметил забытый храм инков. Храм выстроен в форме правильной
усечённой пирамиды с квадратными основаниями сторона нижнего основания равна 2048 и.е., сторона верхней площадки равна
486 и.е. (и.е. инкские единицы длины). Высоту храма путешественник измерить не сумел, поэтому посадил вертолёт на
верхней площадке и начал спускаться по боковой поверхности пирамиды, начиная от угла. Спускался он не напрямую —
склон для этого слишком крут — а наискосок, по линии, угол наклона которой к поверхности земли равен Когда он
добирался до бокового ребра, он переходил через ребро и шёл по следующей грани, под таким же углом
к поверхности
земли.
Он закончил спуск ровно у вершины нижнего основания пирамиды, насчитав по пути 5 сторон (иными словами, его путь выглядит как ломаная, и в этой ломаной получилось 5 отрезков). Какой высоты (в и.е.) был храм?
Источники:
Подсказка 1
Пусть сторона нижнего основания пирамиды равна a, сторона верхнего — b, угол спуска равен α, число пройденных граней равно n. Попробуйте ввести и выразить неизвестные. Что мы хотим найти?
Подсказка 2
Нас интересует высота храма. Обозначим ее за H. Через какой угол ее можно выразить?
Подсказка 3
Обозначим угол наклона боковой стороны пирамиды к земле через β. Выразите H через tg(β).
Подсказка 4
H = (a - b) ⋅ tg(β) / 2. Далее будем считать, что первооткрыватель поднимался, а не спускался. Что можно сказать о линиях, по которым двигался первооткрыватель?
Подсказка 5
Из подобия, первооткрыватель будет проходить по каждой грани меньшее расстояние. Будем считать, что переход по следующей грани будет равен некоторому q, умноженному на длину перехода по предыдущей грани. Какие подобные фигуры мы получим на гранях?
Подсказка 6
У нас получатся подобные трапеции с основаниями a и aq, aq и aq², aq² и aq³ и т.д.. У последней трапеции верхнее основание будет равно b, выразите q.
Подсказка 7
Так как b = aqⁿ, то q = (b / a)¹ᐟⁿ. Обозначьте высоту, на которую первооткрыватель поднялся по первой трапеции, за h. Выразите через эту величины H.
Подсказка 8
H = h + qh + ... + qⁿ⁻¹h. Найдите сумму геометрической прогрессии.
Подсказка 9
Она будет равна (h(a-b)) / (a(1-q)). Заметим, что в этом выражении нам известно все, кроме h. Введем обозначения: ребро, с которого начался подъем — AB, путь начат из A, первый отрезок пути соединяет точки A и P на боковом ребре. Из точки P проведем в плоскости ABP прямую, параллельную AB, она пересечет другое боковое ребро в точке P₁. Получим трапецию с основаниями a и aq. Попробуйте сделать некоторые построения и выразить h.
Подсказка 10
Ортогонально спроецируем точку P на основание пирамиды, получим точку R, тогда PR = h. Попробуйте выразить h через некоторый треугольник.
Подсказка 11
От точки R в плоскости основания проведите перпендикуляр к AB, пусть у нас получится точка L на AB.
Подсказка 12
Заметим, что ∠RBA = 45°, так как R падает на диагональ квадрата, являющегося основанием пирамиды. Что из этого следует?
Подсказка 13
Тогда LB = LR. Выразите h через LR.
Подсказка 14
LR = h / tg(β). Что еще можно заметить в треугольнике ALR?
Подсказка 15
AR = h / tg(α), AL = a - h / tg(β). А еще этот треугольник - прямоугольный. Запишите для него теорему Пифагора.
Подсказка 16
Можно решить квадратное уравнение относительно 1/h.
Подсказка 17
1/h = (1 / (a⋅tg(β))) ⋅ (1 + 1/tg(α) ⋅ √(tg²(β) - tg²(α))). Можем ли мы воспользоваться одним из свойств трапеции?
Подсказка 18
LB = 1/2 ⋅ (AB - PP₁). Подставьте известные нам величины.
Подсказка 19
В итоге получим, что 1/h = 2 / (a ⋅ (1 - q) ⋅ tg(β)). Но мы ведь и до этого получали 1/h.
Подсказка 20
Тогда 1/h = (1 / (a⋅tg(β))) ⋅ (1 + 1/tg(α) ⋅ √(tg²(β) - tg²(α))) = 2 / (a ⋅ (1 - q) ⋅ tg(β)) = 1/h.
Получим, что tg(β) = tg(α) ⋅ √((2(1+q²) / (1-q)²). Вспомните, чему равняется H.
Подсказка 21
Так как H = h(a-b) / (a(1-q)), h = a⋅(1-q)⋅tg(β)/2, и мы нашли tg(β), можем выразить H и подставить значения из условия задачи.
Пусть сторона нижнего основания пирамиды равна сторона верхнего равна
угол спуска равен
а число пройденных граней равно
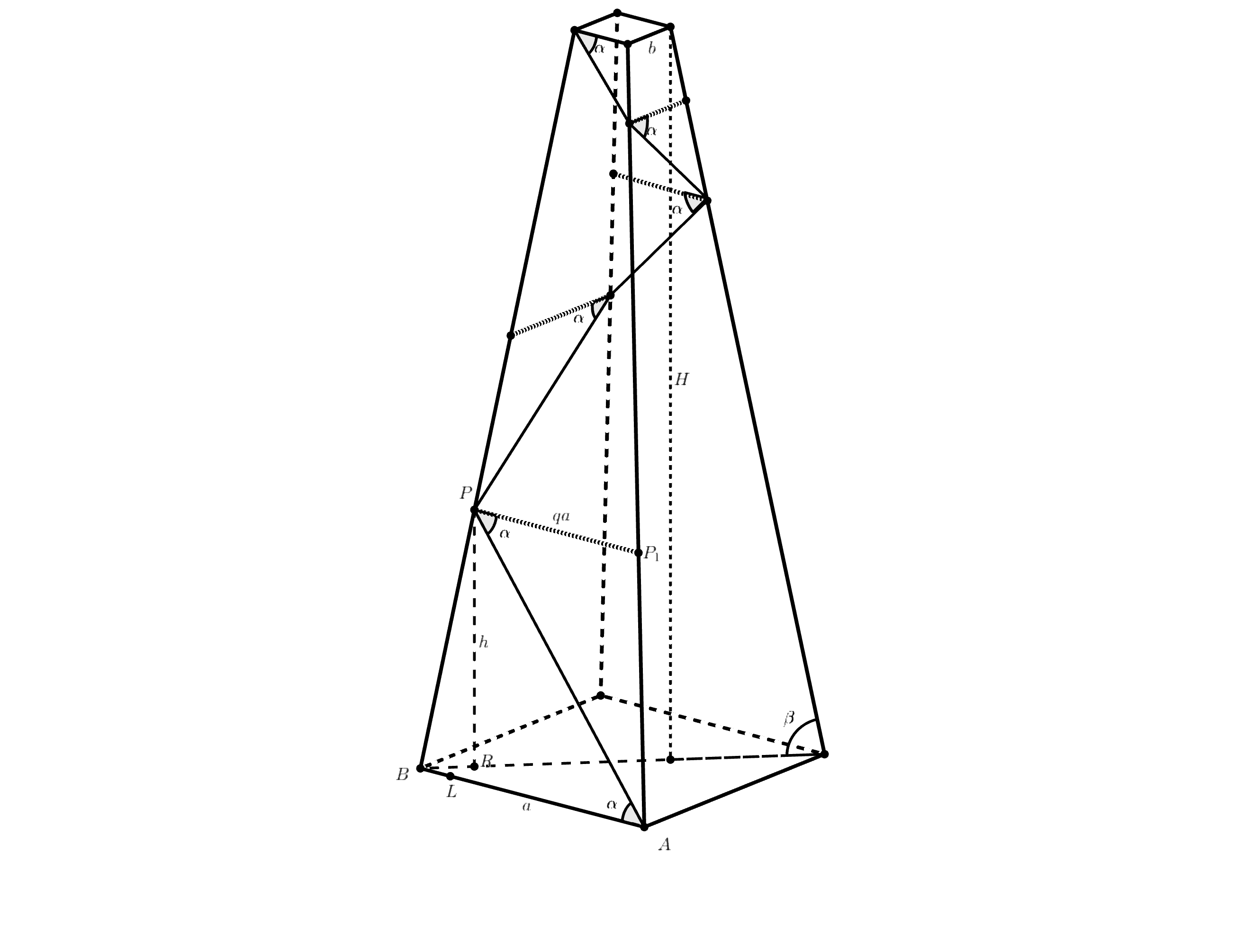
Будем считать, что первооткрыватель поднимался. Обозначим (пока неизвестные нам) величины — высоту постройки через угол
наклона боковой стороны пирамиды к земле через
Тогда
Посмотрим на пирамиду в проекции сверху.
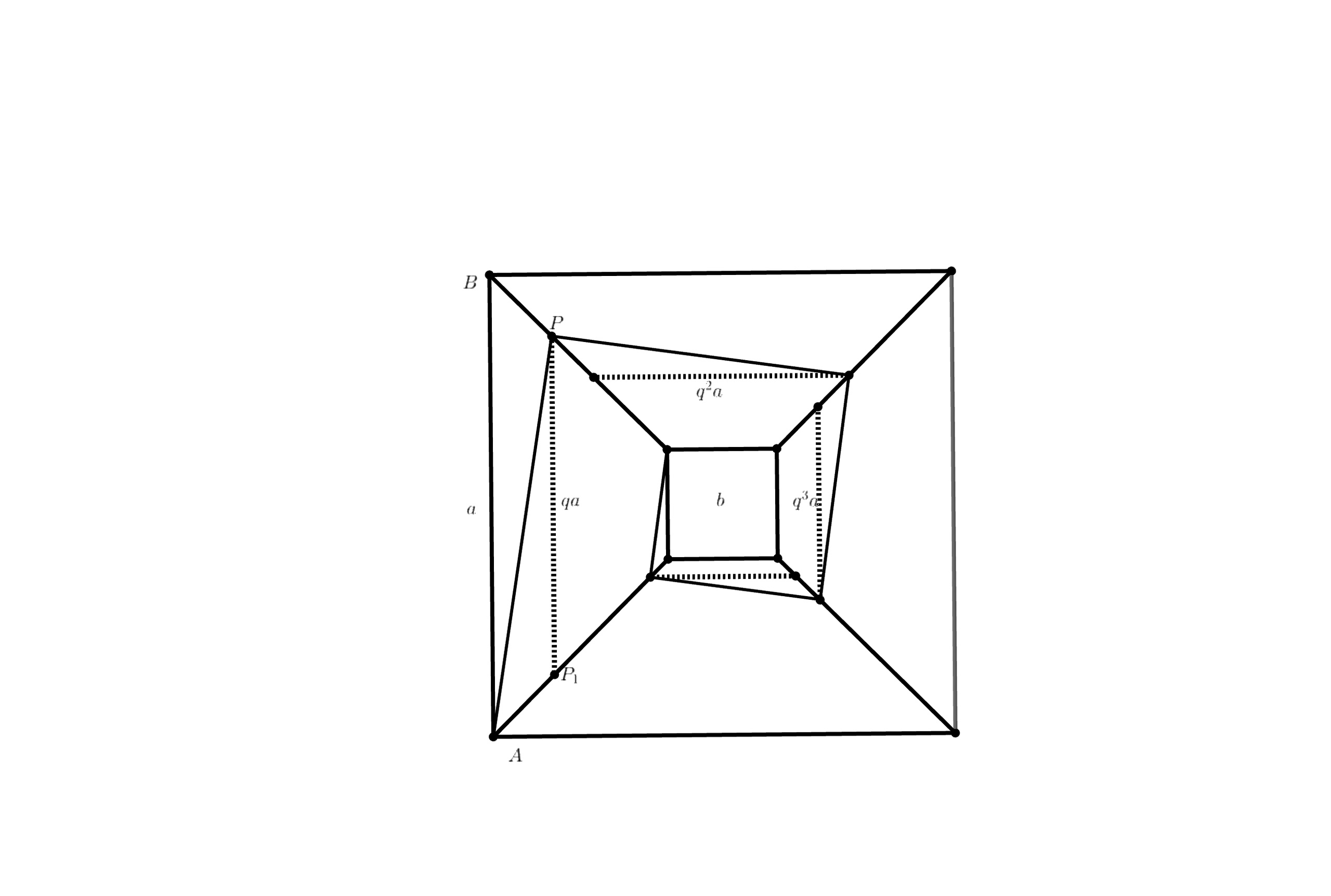
Заметим, что рисунки на гранях подобны друг другу — поднимаясь, первооткрыватель будет проходить по каждой грани все меньшее
расстояние, при том переход по следующей грани будет равен некоторому умноженному на длину перехода по предыдущей
грани.
У нас есть трапеции с основаниями и
и
и
и так далее. У последней трапеции верхнее основание будет равно
следовательно,
Обозначим высоту, на которую первооткрыватель поднялся по первой трапеции, за Тогда из подобия следует, что за второй переход
он добавит к высоте
за третий —
и так далее. Тогда
Нам известны все величины, кроме
Обозначим на пирамиде некоторые точки. Ребро основания, с которого начат подъем — это путь начат из
Первый отрезок пути
соединяет точки
и
на боковом ребре.
Из точки проведем в плоскости
прямую, параллельно
она пересечет другое боковое ребро в точке
Получится
трапеция
с основаниями
Точку
ортогонально спроецируем на основание пирамиды — получим точку
От точки
в плоскости основания пирамиды проведем перпендикуляр к
он пересечет
в точке
Тогда угол равен
так как R падает на диагональ квадрата, являющегося основанием пирамиды.
а
Кроме того,
Треугольник прямоугольный, поэтому
Решим квадратное уравнение относительно
Положительным решением будет
По свойствам трапеции
то есть
Тогда
Вспомним, что
Так как
можем подставить Получим
где
По условию,
В итоге
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




