Тема ПЛАНИМЕТРИЯ

Треугольники и их элементы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела планиметрия

Разделы подтемы Треугольники и их элементы

Точка и отрезок

Медианы

Высоты

Биссектрисы

Средняя линия и её свойства

Ортоцентр и его свойства

Лемма 255

Симедианы

Прямая Эйлера

Прямая Симсона

Ортологичные треугольники: теоремы Карно и Штейнера

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#76808

Дан треугольник $ABC.$ Обозначим через $I,I,I a b c$ центры вневписанных окружностей, касающихся сторон $BC,CA$ и $AB$ соответственно. Докажите, что треугольники $ABC$ и $IaIbIc$ ортологичны.

Показать доказательство

Т.к. $I b$ и $I c$ лежат на внешней биссектрисе угла $A,$ а $I a$ — на внутренней, то $II ⊥ AI . bc a$ Аналогично, $II ⊥ CI,I I ⊥BI . a b c ac b$ Получается, что $ABC$ — ортотреугольник треугольника $IaIbIc.$ А значит, $ABC$ и $IaIbIc$ ортологичны.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76809

В треугольник $ABC$ вписана окружность. Из середины каждого отрезка, соединяющего две точки касания, проводится перпендикуляр к противолежащей стороне. Докажите, что эти перпендикуляры пересекаются в одной точке.

Показать доказательство

Пусть $A ,B ,C 0 0 0$ — точки касания вписанной окружности со сторонами $BC, AC$ и $AB$ соответственно, a $A′,B′,C′$ — середины $B0C0,A0C0,A0B0$ соответственно.

$PIC$

Очевидно, что $AA′ ⊥ B0C0,$ а $B0C0 ∥B′C′.$ Получается, что $AA ′⊥ B′C′.$ Аналогично получается, что $BB ′ ⊥ A′C ′$ и $CC ′ ⊥A ′B′.$ Но $AA′,BB′,CC ′$ пересекаются в одной точке как биссектрисы $ABC.$ Получается, что перпендикуляры из вершин $ABC$ на соответствующие стороны $A′B′C′$ пересекаются в одной точке. Значит, по теореме Штейнера перпендикуляры из вершин $A′B′C ′$ на стороны $ABC$ тоже пересекаются в одной точке.

Ошибка.
Попробуйте повторить позже

Задача 3#76810

В остроугольном треугольнике $ABC$ на высоте $BH$ выбрана произвольная точка $P.$ Точки $A′$ и $C ′$ — середины сторон $BC$ и $AB$ соответственно. Перпендикуляр, опущенный из $′ A$ на $CP,$ пересекается с перпендикуляром, опущенным из $′ C$ на $AP,$ в точке $K.$ Докажите, что точка $K$ равноудалена от точек $A$ и $C.$

Показать доказательство

Пусть $B ′$ — середина $AC.$ Рассмотрим треугольники $A′B′C′$ и $AP C.$ Докажем их ортологичность. Проведем перпендикуляры из вершин второго треугольника на стороны первого. Соответствующими перпендикулярами будут $AP,CP$ и $BP$ ( $′ ′ BP ⊥ AC,AC ∥A C$ ). Они все пересекаются в одной точке $P.$ Значит, треугольники ортологичны.

$PIC$

Тогда опустим перпендикуляры из вершин первого треугольника на стороны второго. Этими перпендикулярами будут $C′K,B′K$ и серединный перпендикуляр к $AC.$ По т. Штейнера они пересекутся в одной точке, т.е. в точке $K.$ Значит, $K$ лежит на серединном перпендикуляре к $AC,$ что доказывает утверждение задачи.

Ошибка.
Попробуйте повторить позже

Задача 4#76811

На стороне $AB$ прямоугольника $ABCD$ вне его построен треугольник $ABE.$ Через точки $C$ и $D$ проведены перпендикуляры $CM$ и $DN$ соответственно к прямым $AE$ и $BE.$ Доказать, что точка $P$ пересечения прямых $CM$ и $DN$ принадлежит прямой, содержащей высоту треугольника $ABE.$

Показать доказательство

Опустим из $E$ перпендикуляр $EK$ на $CD.$ А из точки $K$ на прямую $AB$ — перпендикуляр $KL.$ Тогда $KL, CM$ и $DN$ пересекаются в одной точке, ортополе $CD$ относительно треугольника $ABE$ (по определению ортопола). Но т.к. $ABCD$ — прямоугольник, то прямые $EK$ и $KL$ совпадают. Тогда получается, что высота $EK,CM$ и $DN$ пересекаются в одной точке.

$PIC$

Замечание. Опустим из вершин $A,B$ и $C$ треугольника $ABC$ соответственно перпендикуляры $AA1,BB1$ и $CC1$ на произвольную прямую $ℓ.$ Тогда перпендикуляр из точки $A1$ на прямую $BC,$ перпендикуляр из точки $B1$ на прямую $AC$ и перпендикуляр из точки $C1$ на прямую $AB$ пересекаются в одной точке $P,$ называемой ортополом прямой $ℓ$ относительно треугольника $ABC.$

Ошибка.
Попробуйте повторить позже

Задача 5#76813

Дан шестиугольник $ABCDEF,$ в котором $AB = BC,CD = DE,EF = FA,$ а углы $A$ и $C$ — прямые. Докажите, что прямые $FD$ и $BE$ перпендикулярны.

Показать доказательство

Т.к. треугольники $ABF$ и $BCD$ прямоугольные, то

2 2 2 2 2 2 BF − BD =AB + AF − BC − CD

Из равенств сторон шестиугольника следует, что

AB2+ AF2 − BC2 − CD2 = (AB2− BC2)+ AF2 − CD2 = AF2− CD2 = EF2− ED2

В итоге получаем, что $BF2− BD2 = EF2− ED2$ Тогда по принципу Карно $BE ⊥ FD.$

Ошибка.
Попробуйте повторить позже

Задача 6#76815

Дан выпуклый четырёхугольник $ABCD$ такой, что $AB = CB$ и $AD =DC.$ Точки $K,L,M$ — середины отрезков $AB,CD$ и $AC$ соответственно. Перпендикуляр, проведённый из точки $A$ к прямой $BC,$ пересекается с перпендикуляром, проведённым из точки $C$ к прямой $AD,$ в точке $H.$ Докажите, что прямые $KL$ и $HM$ перпендикулярны.

Показать доказательство

$KM$ — средняя линия в треугольнике $ABC,$ а $ML$ — в треугольнике $ACD.$ Тогда $KM ∥BC$ и $ML ∥AD.$ Т.к. $AH ⊥ BC$ и $CH ⊥ AD,$ то $KM ⊥AH$ и $CH ⊥ ML.$

$PIC$

Применим принцип Карно для четверок точек $(A,H,K, M)$ и $(C,H,L,M ):$

( { HK2 − HM2 = AK2− AM2 ( HL2− HM2 =CL2 − CM2

Вычтем из первого второе. Учитывая, что $M$ — середина $AC,$ получим:

HK2 − HL2 = AK2− AM2 − CL2+ CM2 = AK2 − CL2

Поскольку $AB = BC$ и $CD = AD,$ то $AK = KM = BC ∕2$ и $CL = ML = AD∕2.$ Подставив в предыдущее выражение, получим: $HK2 − HL2 =MK2 − ML2.$ Что по принципу Карно доказывает перпендикулярность $HM$ и $KL.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#76816

Дан равнобедренный треугольник $ABC$ ( $AB = CB$ ). Точка $M$ — точка пересечения биссектрисы угла $B$ и описанной окружности треугольника $ABC.$ На продолжении стороны $AC$ за точку $C$ отметили точку $D.$ На продолжении $AB$ за точку $B$ и $BC$ за точку $C$ отметили точки $E$ и $F$ так, что $BDEF$ — параллелограмм. Доказать, что $MB$ перпендикулярно $EF.$

Показать доказательство

$PIC$

Т.к. треугольник $ABC$ равнобедренный, то $BM$ — диаметр описанной окружности, а значит, $∠BAM = ∠BCM = 90∘.$

EM2 − ED2 = EA2 +AM2 − ED2

Поскольку $ED ∥BC,$ a $ABC$ равнобедренный, то $ED = EA.$ Получаем $EM2 − ED2 = AM2.$

FM2 − F D2 = FC2 +CM2 − FD2

Поскольку $FD ∥AB,$ a $ABC$ равнобедренный, то $FD = FC.$ Получаем $2 2 2 FM − FD =CM .$

Т.к. $AM = MC,$ то получим, что $2 2 2 2 2 2 EM − ED = AM = CM = FM − F D .$ По принципу Карно $EF ⊥ MD.$

Ошибка.
Попробуйте повторить позже

Задача 8#79117

Точки $M$ и $N$ — середины сторон $AB$ и $BC$ соответственно треугольника $ABC.$ На продолжении отрезка $CM$ за точку $M$ отмечена точка $D.$ Оказалось, что $BC = BD = 2$ и $AN =3.$ Докажите, что $∘ ∠ADC = 90.$

Показать доказательство

$PIC$

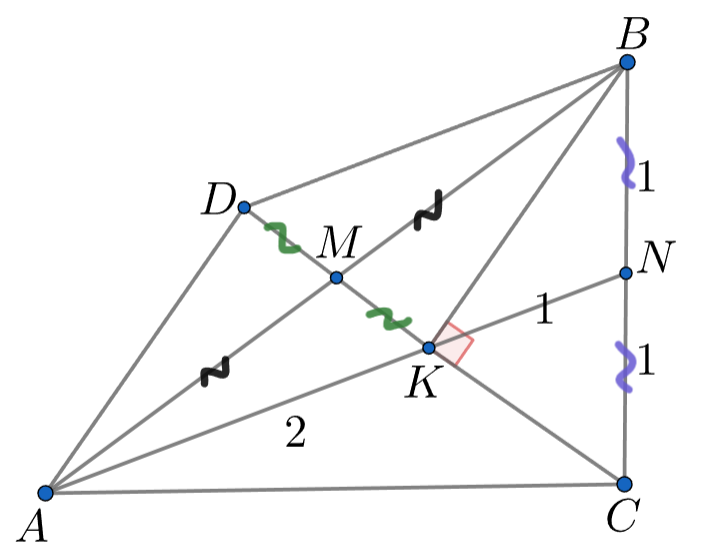
Обозначим через $K$ точку пересечения медиан $AN$ и $CM.$ По свойству медиан $KC = 2KM$ и $AK = 2KN.$ Поскольку к тому же $AN = 3,$ то $KN = 1.$ Таким образом в треугольнике $BKC$ медиана к стороне $BC$ равна $1= BC∕2,$ поэтому $∠BKC = 90∘.$ Это означает, что $BK$ — высота треугольника $BCD,$ в котором $BD = BC.$ Следовательно, $BK$ — его медиана. Поэтому $DK = KC = 2KM,$ откуда $KM = DK ∕2= DM.$ Получается, что диагонали четырехугольника делятся точкой пересечения пополам, то есть $ADBK$ — параллелограмм. Значит, $BK ∥AD.$ откуда $∠ADC = ∠BKD =90∘$ , что и требовалось доказать.

Ошибка.
Попробуйте повторить позже

Задача 9#80746

Пусть длины сторон треугольника являются натуральными числами $a,b,c$ , и одна из его высот равна сумме двух других. Доказать, что число $2 2 2 a + b+ c$ является точным квадратом (натурального числа).

Источники: Всесиб-2024, 11.3 (см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1

Нам нужно как-то записать условие на то, что одна высота равна сумме двух других. Через что тогда можно выразить высоту, чтобы равенство не хотелось сразу стереть из-за его громоздкого вида?

Подсказка 2

Верно, через площадь треугольника и сторону. Тогда наше равенство будет выглядеть как 2S/a = 2S/b + 2S/c => 1/a = 1/b + 1/c => bc = ab + ac. Если мы хотим сказать, что сумма квадратов сторон равна точному квадрату, то давайте подумаем какому конкретно квадрату это может быть равно(квадрат, который выражен через a,b,c).

Подсказка 3

Действительно, подходит квадрат (b + c - a)^2, ведь раскрывая скобки, мы получим, что a^2 + b^2 + c^2 + 2bc - 2ab - 2ac = a^2 + b^2 + c^2, так как bc = ab + ac. Что и требовалось доказать.

Показать доказательство

Пусть $S$ — площадь треугольника, а $h,h ,h a b c$ — высоты к сторонам $a,b,c$ соответственно.

Из формулы площади треугольника имеем, что

2S 2S 2S ha = a-,hb = b-,hc =-c

Без ограничения общности будем считать, что $ha = hb+hc$ . Тогда

1 1 1 a = b +c

Откуда $bc= ac+ ab$ . Но тогда $2bc= 2ac+2ab$ и можно сказать, что

a2+ b2 +c2 = a2+ b2+ c2+2bc− 2ac− 2ab= (b+ c− a)2

Ошибка.
Попробуйте повторить позже

Задача 10#82777

В треугольнике $ABC$ сторона $AC$ наименьшая. На сторонах $AB$ и $BC$ взяты точки $K$ и $L$ соответственно, причём $KA = AC = CL.$ Пусть $M$ — точка пересечения $AL$ и $KC,$ а $I$ — точка пересечения биссектрис треугольника $ABC.$ Докажите, что прямая $MI$ перпендикулярна прямой $AC.$

Подсказки к задаче

Подсказка 1

Что можно сказать про треугольник АСК?

Подсказка 2

Верно, он равнобедренный! А биссектриса AI равнобедренного треугольника — это вкусно. Воспользуйтесь тем, что это больше, чем биссектриса!

Подсказка 3

Биссектриса, проведённая к основанию в равнобедренном треугольнике, также является медианой и высотой. Что можно сказать про прямые AI и СК?

Подсказка 4

Верно, они перпендикулярны! Проведите подобные рассуждения для биссектрисы СI треугольника ACL.

Подсказка 5

Посмотрите на треугольник ACM. Что в нем является высотами? А что еще проходит через точку пересечения высот?

Подсказка 6

Да, это третья высота! MI является высотой и как раз перпендикулярна тому, что нам нужно! А значит, задача решена!

Показать доказательство

По условию $AC = AK,$ значит, $△ ACK$ — равнобедренный, тогда биссектриса $AI$ равнобедренного треугольника $ACK$ также является его высотой, то есть $AI ⊥ CK.$

Аналогично $CI$ является высотой равнобедренного треугольника $ACL,$ то есть $CI ⊥AL.$

$PIC$

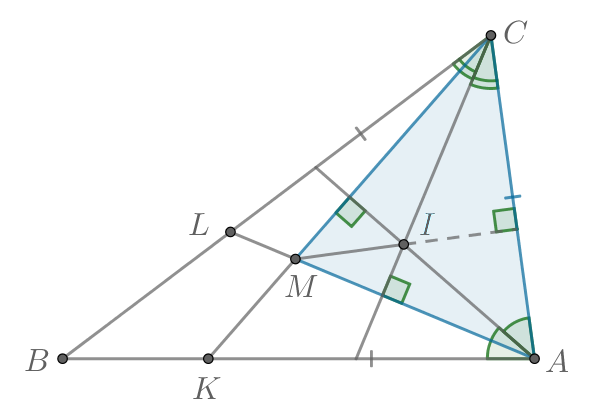
Рассмотрим треугольник $ACM.$ В нем $AI$ и $CI$ — высоты, значит, $I$ — ортоцентр треугольника $ACM,$ следовательно, $MI$ — его третья высота, то есть $MI ⊥AC.$

Ошибка.
Попробуйте повторить позже

Задача 11#83235

В остроугольном треугольнике $ABC$ проведены биссектриса $BL$ и высота $BK.$ Прямые $BL$ и $BK$ пересекают вторично описанную окружность треугольника $ABC$ в точках $W$ и $T$ соответственно. Оказалось, что $BC = BW.$ Докажите, что $TL ⊥ BC.$

Источники: КМО - 2024, вторая задача второго дня для 10-11 классов, автор Шурыгин В.Е. (cmo.adygmath.ru)

Показать доказательство

Из вписанности $∠BAL =∠BAC =∠BW C$ . Получается, что в треугольниках $BAL$ и $BW C$ равны две пары соответствующих углов, значит, равные углы и в третьей паре: $∠BLA = ∠BCW$ . Но из условия $BC = BW$ следует $∠BW C = ∠BCW$ , отсюда $∠BAL = ∠BLA.$

$PIC$

Получается, что треугольник $BAL$ равнобедренный $(BA = BL )$ , тогда $BT$ — его ось симметрии. Значит, $∠BTL =∠BT A$ . Но $∠BT A= ∠BCA =90∘− ∠CBK$ . Видим, что $∠BTL = 90∘− ∠CBT$ , откуда $TL⊥ BC.$

Замечание.

После установления симметрии треугольника $BAL$ относительно $BT$ , можно завершить решение разными способами. Например, заметив, что

∠TCW + ∠CW B =∠T BW + ∠CAB = ∠TBA +∠CAB = 90∘.

Тогда $CT ⊥ BW$ , и в силу $CK ⊥ BT$ , получаем, что $L$ — точка пересечения двух высот в треугольнике $BCT.$ Значит, $TL$ — третья высота, то есть $TL ⊥ BC.$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#83839

Вершину треугольника соединили с точкой, делящей его противоположную сторону в отношении $2:1$ . Докажите, что получившийся отрезок разбивает данный треугольник на два треугольника, у которых есть по равной медиане.

Показать доказательство

Нам дан треугольник $ABC,$ в котором точка $K$ делит $AC$ в отношении $AK :KC = 2:1.$ Рассмотрим медианы $KT$ и $CP$ в треугольниках $ABK$ и $KBC$ соответственно.

$PIC$

$T$ и $P$ — середины $AB$ и $BK$ соответственно, следовательно, $TP$ — средняя линия треугольника $ABK.$ Тогда $AK :TP = 2:1$ и $AK ∥ TP,$ но $AK :KC =2:1,$ значит, $TP = KC$ и $TP ∥KC.$ Следовательно, $KTP C$ — параллелограмм, поэтому $KT = CP.$

Ошибка.
Попробуйте повторить позже

Задача 13#83841

Точки $P$ и $Q$ — середины сторон выпуклого четырехугольника $ABCD$ . Отрезки $AP$ и $AQ$ делят диагональ $BD$ на 3 равные части. Докажите, что $ABCD$ — параллелограмм.

Показать ответ и решение

Обозначим точки пересечения $AP$ и $AQ$ с диагональю $BD$ как $X$ и $Y$ соответственно, тогда $BX = XY = YD.$ Рассмотрим треугольник $BY C,$ заметим, что $XP$ — средняя линия, т.к. $BX =XY$ и $BP = PC.$ Следовательно $XP ∥CY.$ Аналогично получаем, что $CX ∥ YQ.$ Значит, $AXCY$ является параллелограммом.

Проведём диагональ $AC.$ $O$ — точка пересечения $AC$ и $XY,$ т.к. $AXCY$ — параллелограмм, то $O$ делит $AC$ и $XY$ пополам.

$PIC$

Но $BX = YC,$ следовательно $O$ делит и $BD$ пополам. $O$ — точка пересечения диагоналей четырехугольника $ABCD,$ делящая их пополам, значит, $ABCD$ — параллелограмм.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 14#84492

Во вписанном четырёхугольнике $ABCD$ точка $O$ — точка пересечения диагоналей. Точка $O 1$ симметрична $O$ относительно $AD$ и лежит на описанной окружности четырёхугольника. Докажите, что $O1O$ — биссектриса угла $BO1C.$

Показать доказательство

Пусть $OO 1$ пересекает $AD$ в точке $T.$

$PIC$

Тогда $AT$ — медиана и высота в треугольнике $AOO1,$ а значит, биссектриса. Откуда дуги $CD$ и $DO1$ равны. Аналогично дуги $AB$ и $CD$ равны. А значит, $O$ — центр вписанной окружности в треугольник $BO1C.$

Ошибка.
Попробуйте повторить позже

Задача 15#84494

В равнобедренном треугольнике $ABC$ из середины основания $AB$ к боковой стороне $AC$ проведен отрезок $DE$ — биссектриса угла $ADC.$ Из точки $E$ на боковую сторону $BC$ опущена высота $EF.$ Докажите, что отрезок $FD$ является биссектрисой угла $EF B.$

Показать доказательство

Пусть $EF$ пересекает $CD$ в точке $X.$

$PIC$

Заметим, что четырёхугольник $BDXF$ вписанный, так как противоположные углы по $90∘.$ Тогда $∠A= ∠B = ∠DXE.$ В треугольниках $AED$ и $XED$ соответственно равны две пары углов, поэтому получаем оставшееся равенство $∠AED =∠XED.$

Тогда $ED$ является биссектрисой внешнего угла $△CEF.$ При этом $CD$ является биссектрисой внутреннего угла $△CEF$ . Значит, $D$ — центр вневписанной окружности треугольника $CEF.$ Значит, $FD$ — биссектриса угла $EFB.$

Ошибка.
Попробуйте повторить позже

Задача 16#84745

В прямоугольном треугольнике $ABC$ с прямым углом $C$ проведена высота $CH.$ Пусть $I,I 1$ и $I 2$ центры вписанных окружностей треугольников $ABC,ACH$ и $BCH$ соответственно. Докажите, что $CI$ перпендикулярно $I1I2.$

Показать доказательство

$PIC$

Заметим, что

∠CAI +∠ACI2 = ∠A-+90∘− ∠BCH--= 90∘ 2 2

А значит, $AI ⊥CI2,$ откуда $I1I ⊥ CI2.$ Аналогично $I2I ⊥ CI1,$ откуда следует, что $I$ это ортоцентр треугольника $AI1I2.$ А значит $CI ⊥I1I2.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#85482

В остроугольном треугольнике $ABC$ высоты $AH ,BH A B$ и $CH C$ пересекаются в точке $H$ . Через точки, в которых окружность радиуса $HHA$ с центром $H$ пересекает отрезки $BH$ и $CH$ , проведена прямая $ℓA$ . Аналогично проведены прямые $ℓB$ и $ℓC$ . Докажите, что точка пересечения высот треугольника, образованного прямыми $ℓA,ℓB,ℓC$ , совпадает с центром окружности, вписанной в треугольник $ABC$ .

Источники: ММО - 2024, второй день, 11.4 (см. mmo.mccme.ru)

Показать доказательство

Покажем, что биссектрисы треугольника $ABC$ содержат высоты треугольника, образованного прямыми $ℓ ,ℓ ,ℓ A B C$ . Для этого докажем, что точка пересечения прямых $ℓB,ℓC$ лежит на биссектрисе угла $∠BAC$ , а прямая $ℓA$ перпендикулярна этой биссектрисе.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямая $ℓA$ перпендикулярна биссектрисе угла $∠BAC$ .

Пусть $R$ и $S$ - это точки пересечения окружности с центром в $H$ радиуса $HHA$ с отрезками $BH$ и $CH$ соответственно. Тогда треугольник $RHS$ - равнобедренный с основанием $RS$ , поэтому прямая $RS$ (она же $ℓA$ ) перпендикулярна прямой $pA$ , содержащей биссектрису угла $∠BHC$ . Поэтому достаточно доказать, что прямая $pA$ параллельна биссектрисе угла $∠BAC$ .

$PIC$

Пусть $MA$ и $NA$ — середины дуг $HCHHB$ и $⌣ HBAHC$ окружности $ωA$ , построенной на $AH$ как на диаметре. Из свойств вписанных углов следует, что $AMA$ — биссектриса $∠BAC,HNA$ — биссектриса $∠HCHHB$ . Заметим также, что $MANA$ - диаметр окружности $ωA$ . Значит, отрезки $MANA$ и $AH$ пересекаются в центре окружности $ωA$ как её диаметры и делятся точкой пересечения пополам. То есть четырёхугольник $AMAHNA −$ параллелограмм (и даже прямоугольник, поскольку его углы - вписанные, опирающиеся на диаметры окружности $ωA$ , то есть прямые). В частности, $AMA ∥HNA$ , что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямые $ℓ B$ и $ℓ C$ пересекаются на биссектрисе угла $∠BAC$ .

Пусть прямые $ℓ B$ и $ℓ C$ пересекают отрезки $BH, CH$ в точках $P$ и $Q$ соответственно, а точку пересечения $ℓ B$ и $ℓ C$ обозначим через $X$ . Также обозначим углы $∠A,∠B$ и $∠C$ треугольника $ABC$ через $2α,2β$ и $2γ$ соответственно.

$PIC$

Поскольку $HP = HHC$ и $HQ = HHB$ , то треугольники $HHCP$ и $HHBQ$ - равнобедренные с углами, равными $∠HCHB = ∠BAC = 2α$ , напротив оснований. Поэтому $∠HP HC = ∠HQHB =90∘− α= β+ γ$ . Пусть прямые $ℓB$ и $ℓC$ пересекают отрезок $AH$ в точках $U$ и $V$ соответственно. Тогда треугольник $PUH$ - равнобедренный с основанием $PU$ , значит $∠XP H = ∠UPH = 180∘−∠2BHA-= γ$ . Рассуждая аналогично для треугольника $QV H$ , получаем, что $∠XQH = β$ . Тогда получаем

∠XP HC =∠HP HC − ∠HP X = β+ γ− γ = β =∠XQHC,

откуда следует, что $X$ лежит на окружности, описанной около треугольника $HCP Q$ . Аналогично точка $X$ лежит на окружности, описанной около треугольника $HBP Q$ . Таким образом, пять точек $X,HB$ , $P,Q,HC$ лежат на одной окружности.

Тогда по свойству вписанных углов $∠XHBHC = ∠XQHC =β$ . Четырёхугольник $BHCHBC −$ вписанный, поскольку $∠BHCC = ∠BHBC = 90∘$ . Значит, $∠HCHBC = 180∘− ∠ABC =180∘− 2β$ , то есть $∠AHBHC = 2β$ . Отсюда следует, что $HBX$ - биссектриса угла $∠AHBHC$ . Аналогично $HCX −$ биссектриса угла $∠AHCHB$ . Значит, точка $X$ является центром окружности, вписанной в треугольник $AHBHC$ , в частности, лежит на биссектрисе угла $∠BAC$ .

_________________________________________________________________________________________________________________________________________________________________________________

Повторяя рассуждения для двух других биссектрис треугольника $ABC$ , получаем, что точка пересечения биссектрис треугольника $ABC$ совпадает с точкой пересечения высот треугольника, образованного прямыми $ℓ ,ℓ ,ℓ . A B C$

Ошибка.
Попробуйте повторить позже

Задача 18#85494

В остроугольном треугольнике $ABC$ проведена высота $AH$ . Точки $M$ и $N$ - середины отрезков $BH$ и $CH$ . Докажите, что точка пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, равноудалена от точек $B$ и $C$ .

Источники: ММО - 2024, первый день, 11.2 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть перпендикуляры через M и N пересекаются в точке P. Тогда над каким дополнительным построением можно подумать, чтобы сделать MP и NP чем-то хорошим? Не забудьте, что M и N являются серединами отрезков.

Подсказка 2

Да, давайте попробуем опустить перпендикуляры X и Y из точки H на стороны треугольника. В таком случае MP и NP являются средними линиями, так как они параллельны основаниям и делят одну из сторон пополам. Но как тогда можно переформулировать вопрос задачи удобным образом для нас?

Подсказка 3

Верно, это значит, что четырёхугольник CXYB должен быть вписанным, так как в таком случае P центр описанной окружности и равноудален от B и C. Теперь только осталось посчитать уголочки, используя вписанный четырёхугольник и равные углы в прямоугольном треугольнике с проведённой высотой. Победа!

Показать доказательство

Первое решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точки, симметричные $B$ и $C$ относительно прямых $MP$ и $NP$ , через $B0$ и $C0$ . Тогда прямые $MP$ и $NP$ — cерединные перпендикуляры к отрезкам $BB0$ и $CC0$ , поэтому достаточно доказать, что четырёхугольник $BB0C0C$ — вписанный.

$PIC$

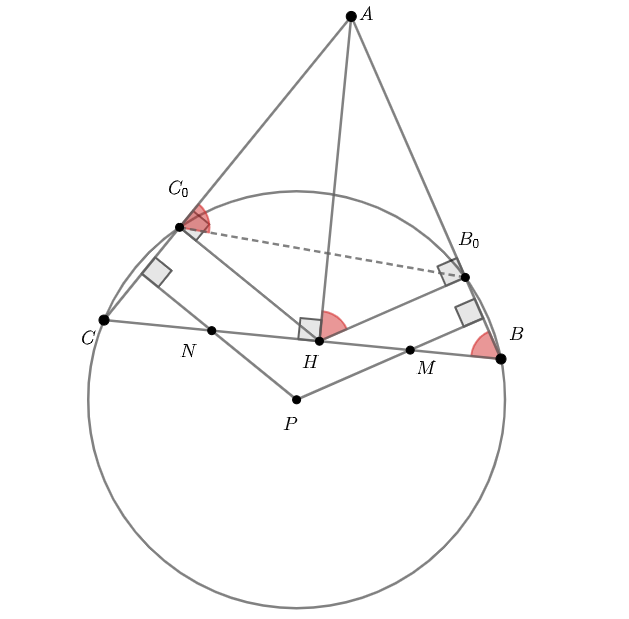
Заметим, что $MP$ и $NP$ содержат средние линии треугольников $BB0H$ и $CC0H$ , параллельные сторонам $B0H$ и $C0H$ соответственно. Значит, $HB0 ⊥ AB,HC0 ⊥ AC.$

Четырёхугольник $HB0AC0$ вписан в окружность, построенную на $AH$ как на диаметре, поэтому $∠B0C0A = ∠B0HA$ по свойству вписанных углов. При этом $∠B0HA =90∘− ∠HAB0 = ∠ABC$ . Значит, четырёхугольник $BB0C0C$ вписанный.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точку пересечения высот треугольника $ABC$ — через $K$ .

$PIC$

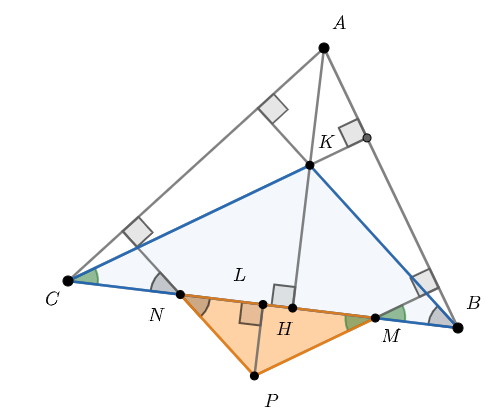
Тогда заметим, что треугольники $△BKC$ и $△NP M$ подобны по двум углам. Действительно, $∠MNP = 90∘− ∠BCA = ∠CBK$ . Аналогично, выполнено равенство $∠NMP = ∠BCK$ . Также заметим, что коэффициент подобия этих треугольников равен $2$ , поскольку $MBNC = 2$ .

Опустим из $P$ перпендикуляр $P L$ на $BC$ . Тогда из доказанного подобия следует, что $HLCM-= 2,$ т. е. $LM = NH$ . Следовательно, $BL = BM + ML = BM + NH = 12BC,$ а значит, $P$ лежит на серединном перпендикуляре к отрезку $BC$ , откуда следует требуемое.

Ошибка.
Попробуйте повторить позже

Задача 19#85508

Точки $P,Q$ лежат внутри окружности $ω$ . Серединный перпендикуляр к отрезку $PQ$ пересекает $ω$ в точках $A$ и $D$ . Окружность с центром $D$ , проходящая через $P$ и $Q$ , пересекает $ω$ в точках $B$ и $C$ . Отрезок $PQ$ лежит внутри треугольника $ABC$ . Докажите, что $∠ACP =∠BCQ$ .

Источники: Турнир городов - 2024, весенний тур, 11.2 (см. turgor.ru)

Подсказки к задаче

Подсказка 1

Про окружность ω пока толком ничего не известно, а вот окружность с центром в D даёт сразу 4 равных отрезка (равенство радиусов) на чертеже. Посмотрите, что из этого можно взять для окружности ω.

Подсказка 2

Так как BD=DC, то дуги ВD и DC в ω равны, значит, AD — биссектриса ∠BAC.

Подсказка 3

Пусть I — точка пересечения отрезка АD и дуги BPQC, тогда по теореме о трилистнике I — центр вписанной в ΔABC окружности. Что же можно взять из этого факта, если в задаче нам нужно доказать равенство углов?

Подсказка 4

Конечно! То, что CI — биссектриса ∠BСА. Для завершения доказательства не хватает равенства ∠PCI и ∠ICQ, но это совсем несложно получить, если Вы ещё не забыли, чем по условию является AD для отрезка PQ.

Показать доказательство

$PIC$

Первое решение.

Пусть $I$ — точка пересечения отрезка $AD$ и дуги $BPQC$ . Так как $DB = DC$ , то $AD$ — биссектриса угла $BAC$ и по теореме о трилистнике $I$ — центр вписанной в треугольник $ABC$ окружности. Следовательно, $CI$ — биссектриса угла $ACB$ . С другой стороны, так как $AD −$ серединный перпендикуляр к $P Q$ , то $PI = QI$ , то есть $CI$ — биссектриса угла $PCQ$ . Из этих двух утверждений следует утверждение задачи.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим $∠ACQ =α,∠QCP = β,∠PCB = γ$ . Необходимо доказать, что $γ = α$ .

Заметим, что

α+ β+ γ = ∠ACB = ∠ADB = ∠BDP +∠PDA

Далее, $∠BDP = 2∠BCP = 2γ$ , как центральный и вписанный в окружность ( $DP Q$ ), а также $∠P DA = 12∠PDQ = 12 ⋅2∠PCQ = β$ , как центральный и вписанный в окружность ( $DPQ$ ). Тогда

α+ β+ γ = ∠BDP + ∠PDA = 2γ+β

γ =α

______________________________________________________________________________________________________________________________________________________

Замечание.

В условии задачи дано, что точки $P$ и $Q$ лежат не только внутри окружности $ω$ , но и внутри вписанного в неё треугольника $ABC$ . Последнее условие на самом деле излишне. Из остальных условий задачи следует, что точки $P$ и $Q$ изогонально сопряжены относительно треугольника $ABC$ . Но если обе изогональные точки лежат внутри описанной окружности, то они лежат и внутри треугольника, поскольку при изогональном сопряжении три сегмента, ограниченные сторонами треугольника и дугами описанной окружности, переходят в три угла, вертикальных углам треугольника

Ошибка.
Попробуйте повторить позже

Задача 20#85553

В остроугольном треугольнике $PVG$ обозначили точку пересечения высот через $H$ , центр описанной окружности через $O$ . Площади треугольников $OHP$ и $OHV$ равны 5 и 3 соответственно. Найдите площадь треугольника $OHG$ .

Источники: ПВГ - 2024, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Итак, на нашем чертеже треугольник и две точки внутри него. Как-то пусто, и совсем не понятно, что с такой картинкой делать. Значит нужно придумать, что еще тут построить. Может быть, отметить какую-нибудь точку так, чтобы о прямой, соединяющей эту точку и центр описанной окружности нам было что-то известно. Что это может быть за точка?

Подсказка 2

Пусть М - середина стороны PV. Тогда ОМ перпендикулярна PV, а GM - медиана треугольника. Пусть GM пересекает отрезок ОН в точке Т. Вот, теперь чертеж выглядит поинтереснее! Рассмотрите его и найдите подобие.

Подсказка 3

Итак, треугольники GHT и OTM подобны. Но с каким коэффициентом? Чтобы это узнать, нужно заметить, что Н - это не абы что, а ортоцентр, и вспомнить его свойства.

Подсказка 4

По свойству ортоцентра GH = 2*OM. Получается, GT : TM = 2 : 1. Как тогда относятся друг к другу площади треугольников GHO и OHM?

Подсказка 5

Так же как 2 к 1! Теперь выразите площадь OHM через известные нам площади. Тут самое главное не забыть рассмотреть случаи!

Показать ответ и решение

В точке $H$ пересекаются три высоты треугольника. Так как $O$ — центр описанной окружности, то в точке $O$ пересекаются серединные перпендикуляры треугольника. Пусть точка $M$ — середина стороны $PV$ , тогда $GM$ медиана. Точка $T$ — точка пересечения медианы и прямой $OH$ .

$PIC$

Треугольники $MOT$ и $GHT$ подобны (следует из параллельности прямых $MO$ и $HG$ , которые обе перпендикулярны прямой $P V$ ). Так как $HG = 2⋅MO$ (этот факт из школьной геометрии хорошо известен как "свойство ортоцентра"), то коэффициент подобия равен 2. Значит, $GT :TM = 2:1$ , то есть медиана $GM$ делится точкой $T$ в отношении $2:1$ . Это означает, что $T$ - точка пересечения медиан треугольника $P VG$ . Поэтому площадь $△OHG$ в 2 раза больше площади $△OHM$ .

Так как $M$ — середина $P V$ , то

S = S△OHP-+S△OHV--⇒ S = S + S . △OHM 2 △OHG △OHP △OHV

Здесь ошибкой был бы вывод о том, что, значит, $S =5+ 3= 8 △OHG$ . Дело в том, что выше доказано, что одна из этих трех площадей является суммой двух других. Но какая именно, зависит от рисунка, который мы сделаем. Важно, где прямая $OH$ пересекает стороны треугольника. Если треугольник $P VG$ правильный, то точки $O$ и $H$ совпадают и указанные в условии задачи три площади вырождаются (это здесь невозможно, так как дано, что площади равны 3 и 5). Если прямая $OH$ проходит через любую вершину треугольника, то тогда одна из трех площадей равна 0 , а две другие — ненулевые, но равны между собой (тоже не наш случай). Если же прямая $OH$ пересекает две стороны (рассмотренный выше случай), то мы доказали, что одна из этих трех площадей (в одном случае это $OHG$ , в другом — $OHP,$ в третьем — $OHV )$ является суммой двух других.