Трапеция
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и
Боковая сторона
равная
перпендикулярна основаниям. На
сторонах
и
взяты соответственно точки
и
такие, что
Найдите все углы треугольника
Источники:
Подсказка 1
Нам дана очень хорошая трапеция, давайте найдём ее углы и попробуем понять что-то хорошее о четырёхугольнике АMCN.
Подсказка 2
Он вписанный! Так как сумма углов MCN и MAN равна 180º. Попробуем найти угол AMN, может на рисунке есть угол, равный ему?
Подсказка 3
Вписанные углы AMN и ACN опираются на одну и ту же дугу, а значит, они равны! А как найти угол ACN? Обратите внимание на равные отрезки, они помогут определить угол ВСА, а зная его, мы легко можем найти ACN, а значит, и все углы треугольника AMN)
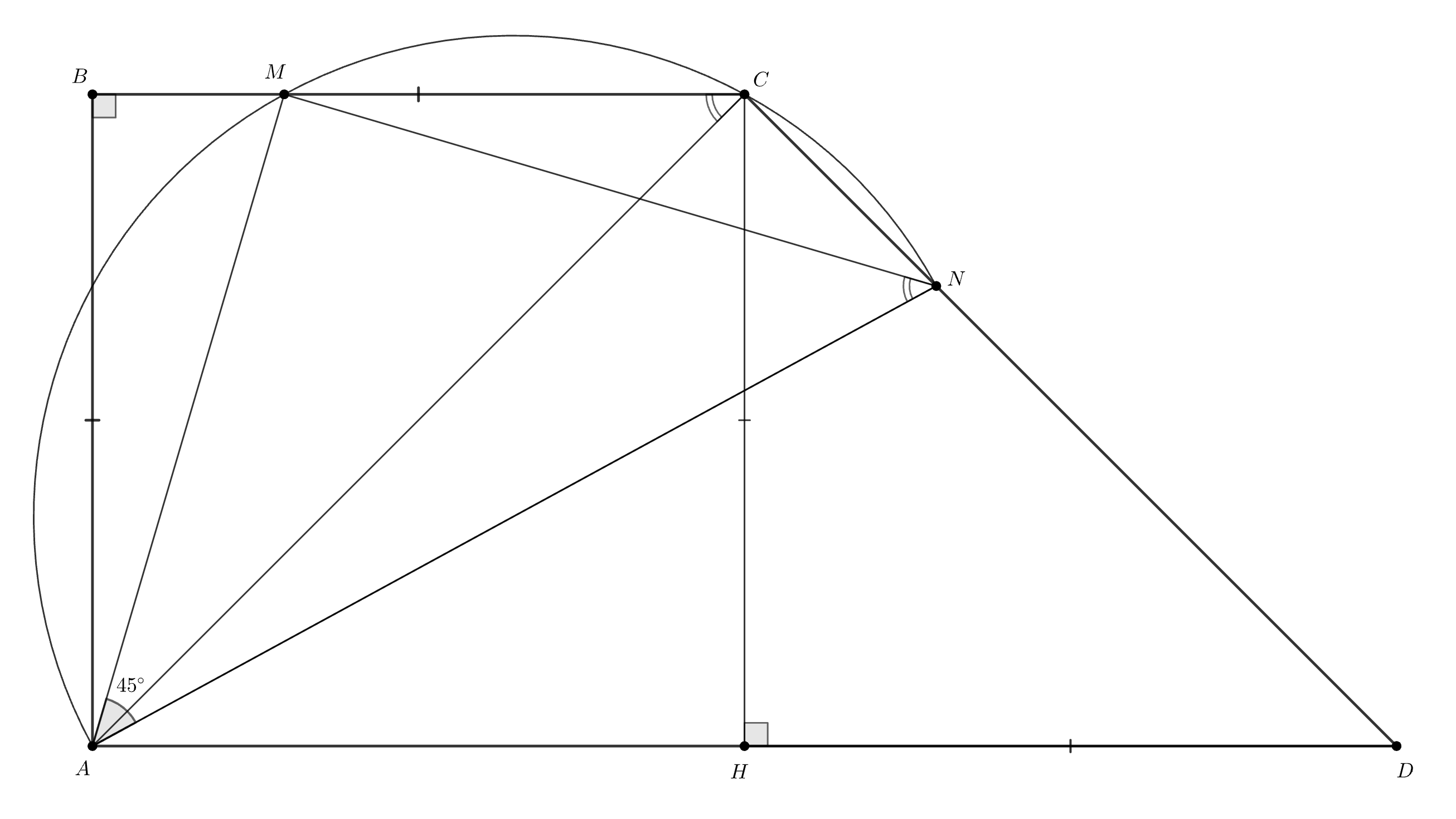
Поскольку и
получаем, что
Проведем высоту
Она будет равна
так как
тогда
Кроме того,
По условию,
так как
четырехугольник
является вписанным.
как вписанные углы, опирающиеся на одну
дугу.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




