Средняя линия и её свойства

Пусть пересекается с в точке

Первое решение.

Прямая, проходящая через середину отрезка параллельно это средняя линия треугольника она равна половине То есть

Прямая, проходящая через точку отрезка параллельно это средняя линия треугольника она равна половине То есть

В итоге

__________________________________________________________________________________________________

Второе решение.

Мы видим медиану и хочется немедленно её удвоить.

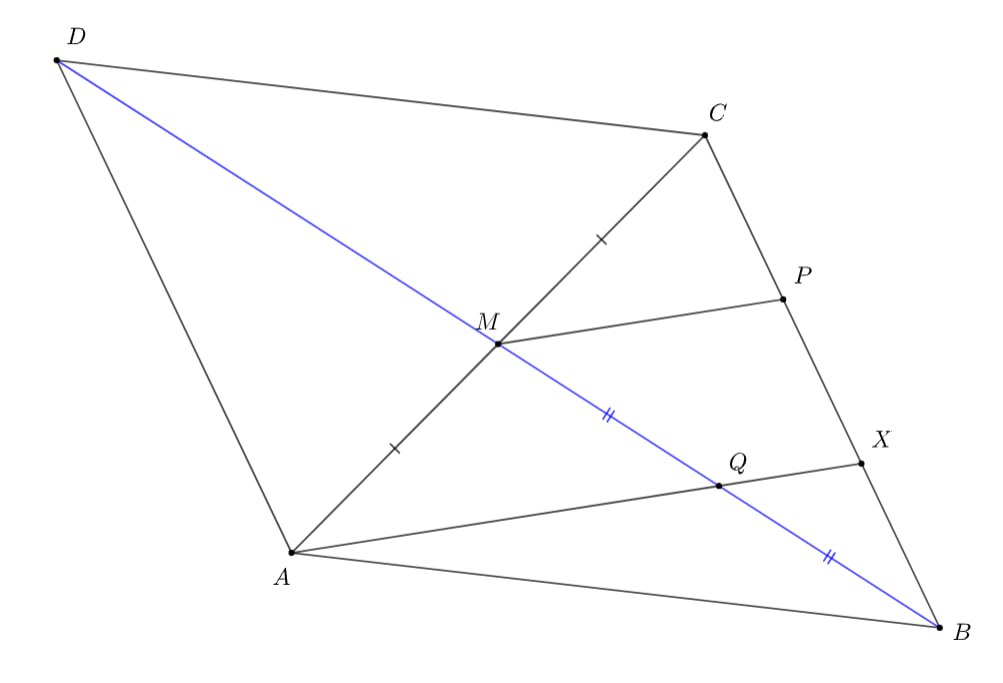
Тогда мы получаем параллелограмм и за счёт равенства накрест лежащих углов при параллельных прямых с коэффициентом подобия

Из подобия мы выяснили, что

Прямая, проходящая через точку параллельно это средняя линия треугольника она равна половине В итоге

__________________________________________________________________________________________________

Третье решение.

По теореме Менелая для треугольника и прямой

По теореме Менелая для треугольника и прямой

Прямая, проходящая через точку параллельно это средняя линия треугольника она равна половине В итоге