Медианы
Ошибка.
Попробуйте повторить позже
На медиану треугольника
опустили перпендикуляр
и перпендикуляр
из некоторой точки
на стороне
(
и
— различные точки, лежащие внутри
Оказалось, что
Докажите, что
Подсказка 1
С суммой BD+AB неудобно работать, было бы удобнее спрямить ее в одну прямую. Для этого продлим АВ на BD за точку А, отметим так точку Е.
Подсказка 2
Нам бы хотелось доказать, что ЕМ параллельно DK, а там еще и равные отрезки отсекаются ими, есть какое-то утверждение, помогающее нам доказать эта параллельность!
Подсказка 3
Теорема Фалеса, например! Таким образом, нашли еще один прямой угол - теперь в треугольнике ЕМВ. Осталось им воспользоваться и доказать требуемое!
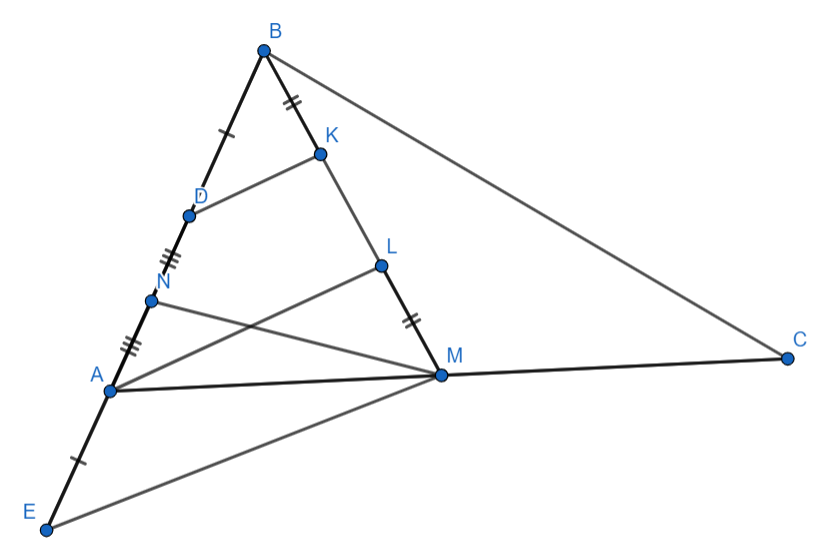
Продлим за точку
на
Из
и
по теореме Фалеса следует
то есть
Пусть
— середина
и
Тогда
как средняя линия, и
как медиана
из прямого угла, откуда и получаем требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




