Биссектрисы
Ошибка.
Попробуйте повторить позже
В неравнобедренном остроугольном треугольнике проведены высота из вершины
и биссектрисы из двух других вершин.
Докажите, что описанная окружность треугольника, образованного этими тремя прямыми, касается биссектрисы, проведенной из вершины
Источники:
Подсказка 1
Давайте обозначим за I точку пересечения биссектриc. Если наша окружность и касается биссектрисы угла A, то только в точке I. Поэтому логично будет применить обратную теорему об угле между касательной и хордой...
Подсказка 2
Давайте обозначим за K- точку пересечения CI и AH, за N- BI и AH. Тогда легко видеть, что уголок ∠IKN=90°-∠ACB/2. Осталось доказать, что∠AIN также равен 90°-∠ACB/2...
Подсказка 3
∠AIN- внешний для треугольника △AIB, где мы знаем уголки ∠IBA=∠ABC/2 и ∠IAB=∠BAC/2. Найдите уголок ∠AIN и завершите решение!
Пусть — центр вписанной окружности
а биссектрисы
пересекают высоту в точках
соответственно. Не умаляя
общности,
и
Отсюда следует
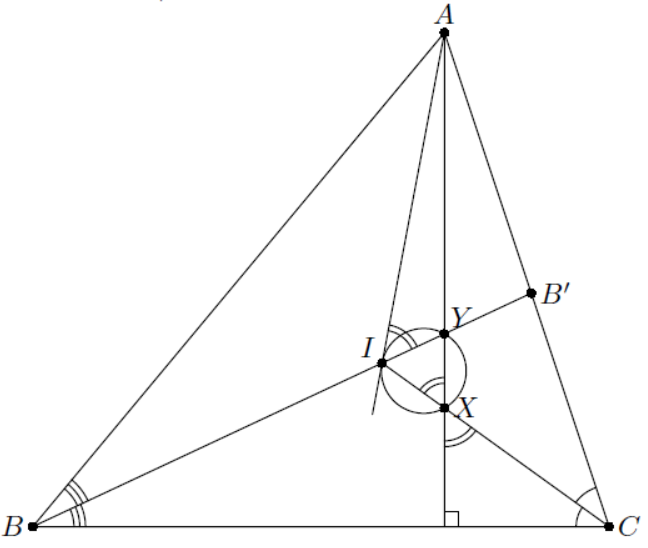
Используем то, что — внешний угол в
Угол между прямой и хордой
равен вписанному углу
опирающемуся на эту хорду. Следовательно,
является
касательной.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




