Параллелограмм
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
параллелограмма
. На отрезке
нашлась такая точка
, что
. Найдите
градусную меру угла
В ответ внесите число.
Источники:
Подсказка 1
У нас есть параллелограмм ABCD и точка E- середина стороны AB. Естественным построением в данном случае будет продление отрезка DE до пересечения с прямой BC. Что же оно нам дает?
Подсказка 2
Пускай луч DE пересекает прямую BC в точке K. Посмотрим на треугольники △AED и △KEB. У них AE=EB и ∠KEB=∠AED. Чего им не хватает, чтобы быть равными?
Подсказка 3
Еще одного уголочка! Но ведь прямые AD и CK параллельны, поэтому ∠EAD=∠EBK ⇒ △AED =△KEB. В частности, BK=AD=BC=BF. Повнимательнее посмотрите на треугольник △KFC и завершите решение!
Продолжим до пересечения с прямой
в точке
. Так как
, то
Кроме того,
и
, значит, равны треугольники
и
Тогда
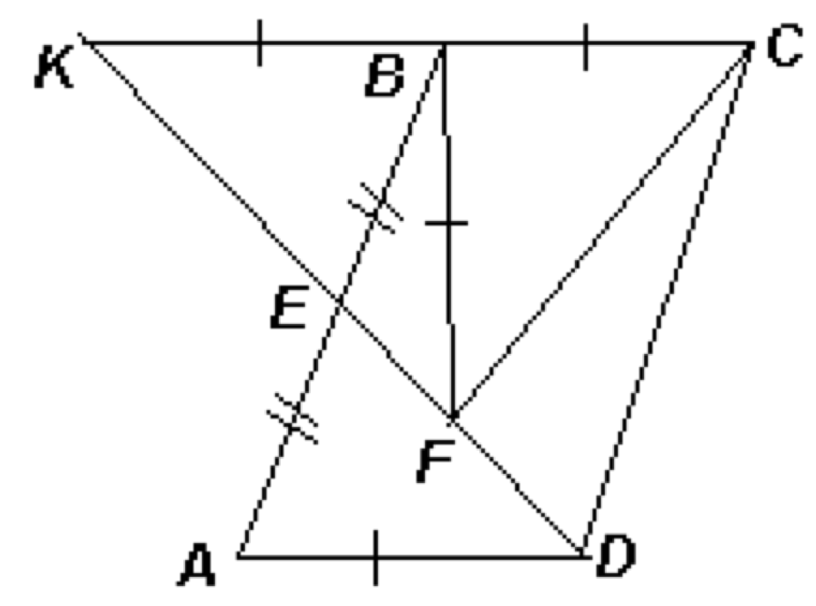
Таким образом, в треугольнике медиана
равна половине стороны, к которой она проведена, поэтому этот треугольник —
прямоугольный с прямым углом
Следовательно, и угол
— прямой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




