Трапеция
Ошибка.
Попробуйте повторить позже
В трапеции оказалось, что
и
Найдите угол
Источники:
Подсказка 1
Сделаем рисунок. Пока не очень понятно, откуда на картинке возьмётся нужное, да и условие про сумму длин двух сторон явного результата не даёт. Значит, надо придумать дополнительные построения! Какие распространённые конструкции Вы знаете?
Подсказка 2
Хочется, чтобы у нас появился ещё один (или не один) отрезок, равный AB + CD. Для этого можно провести прямые через середину боковой стороны BC и оставшиеся вершины трапеции. Что интересного можно сказать о треугольниках, полученных в результате пересечения проведённых прямых с прямыми, содержащими основания трапеции?
Подсказка 3
Итак, у нас образовался четырёхугольник с тремя равными и двумя параллельными сторонами. Это ...?
Подсказка 4
Докажите, что это параллелограмм. Подумайте, в каком параллелограмме могут быть равны 3 стороны.
Подсказка 5
Тут уже неплохо считаются многие углы, но чего-то всё равно не хватает. Попробуем добавить в конструкцию ещё равнобедренных треугольников, а может и более "интересных", например, ... . Отразите точку B относительно диагонали ромба.
Подсказка 6
Осталось лишь увидеть тот самый равносторонний треугольник, ещё немного поработать с углами и симметрией и наслаждаться победой!
Отметим середину стороны точку
Продлим луч
до пересечения с прямой
в точке
и луч
до пересечения с
прямой
в точке
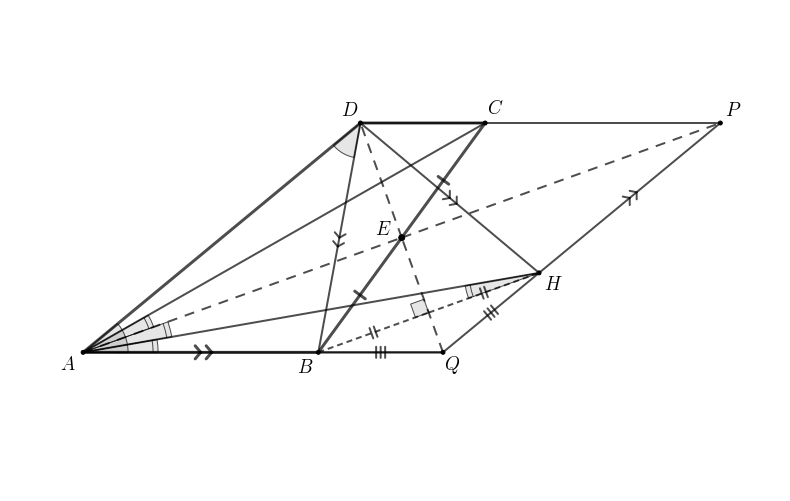
Из равенства треугольников и
получаем, что
Откуда — равнобедренный треугольник. Аналогично равны треугольники
и
откуда равнобедренным является
треугольник
Получаем, что четырёхугольник
является ромбом.
Отразим точку относительно диагонали
получим точку
Так как
То и
Получаем, что в равнобедренном треугольнике
угол
равен
значит, треугольник
равносторонний.
Треугольник равнобедренный, поэтому
то есть трапеция
равнобедренная. Из этого получаем,
что
То есть
В силу симметрии в ромбе
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




