Трапеция
Ошибка.
Попробуйте повторить позже
Диагонали и
равнобокой трапеции
пересекаются в точке
. Известно, что
:
. Окружность
с
центром
, проходящая через вершины
и
, пересекает продолжение основания
за точку
в точке
. Оказалось, что
. Найдите отношение основания
к радиусу окружности
.
Источники:
Подсказка 1
Давайте попробуем выразить каким-либо образом основание через радиус, чтобы в результате отношения радиусы сократились. Давайте проведем высоту из точки O на основание AD, тогда из прямоугольного треугольника мы можем найти, что AD = 2*AO*cos∠DAO. Таким образом, отношение AD к радиусу окружности будет равно 2cos∠DAO. Подумайте, откуда мы можем найти косинус данного угла?
Подсказка 2
Давайте обратим свое внимание на треугольник KBO, всё таки про него нам довольно много известно из условия. Он равнобедренный, а его сторона OK равна OA и OD. По условию нам дано отношение оснований нашей равнобокий трапеции. Подумайте, как, используя данное отношение, мы можем выразить KB и BO через сторону OK.
Подсказка 3
Если воспользоваться тем, что OK=OA=OD и тем, что △AOD подобен △BOC, можем найти, что BO=KB=2*OK/3. По сути, нам известны три стороны одного треугольника, выраженные через одну и ту же переменную, просто с разными коэффициентами. В таких случаях очень удобно использовать теорему косинусов. Давайте воспользуемся ей для угла KBO, так как ∠KBO = 180 - ∠OBC = 180 - ∠DAO. Таким образом, мы легко находим 2cos∠DAO.
Обозначим радиус окружности за ,
. Из
получаем
(с учётом условия
задачи).
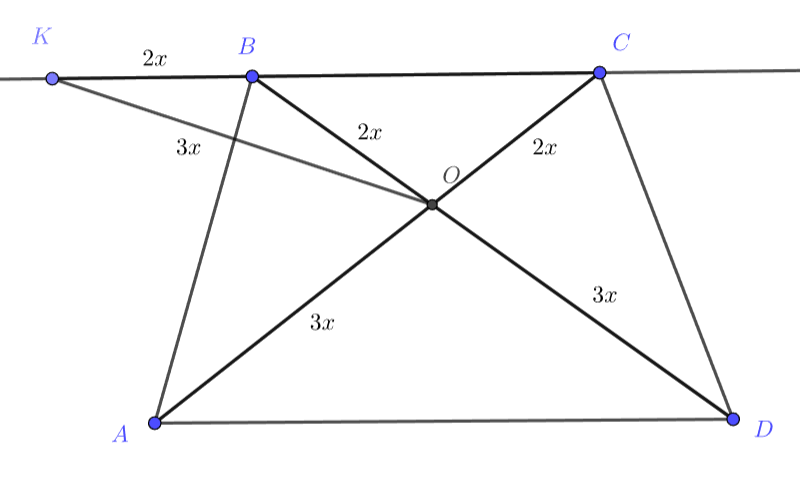
По теореме косинусов для
Если провести высоту треугольника , то легко понять, что
, отсюда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




