Трапеция
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На сторонах и
равнобедренной трапеции
с основаниями
и
отметили точки
и
соответственно. Оказалось, что
— параллелограмм. Докажите, что
где
и
— середины сторон
и
соответственно.
Отметим центр параллелограмма
Он лежит на средней линии
трапеции, поскольку
Продлим
до
пересечения с
и
в точках
и
соответственно. Заметим, что
и
а значит
потому что
Также отметим, что
Теперь видно, что
по первому признаку, а значит у них
равные высоты
и
проведённые к
и
В силу равнобедренности трапеции
Но тогда
а вместе с этим
Следовательно,
что и требовалось.
Ошибка.
Попробуйте повторить позже
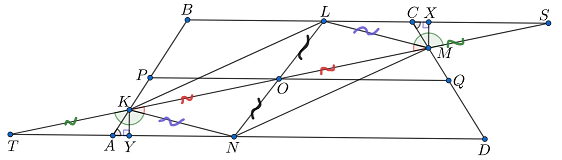
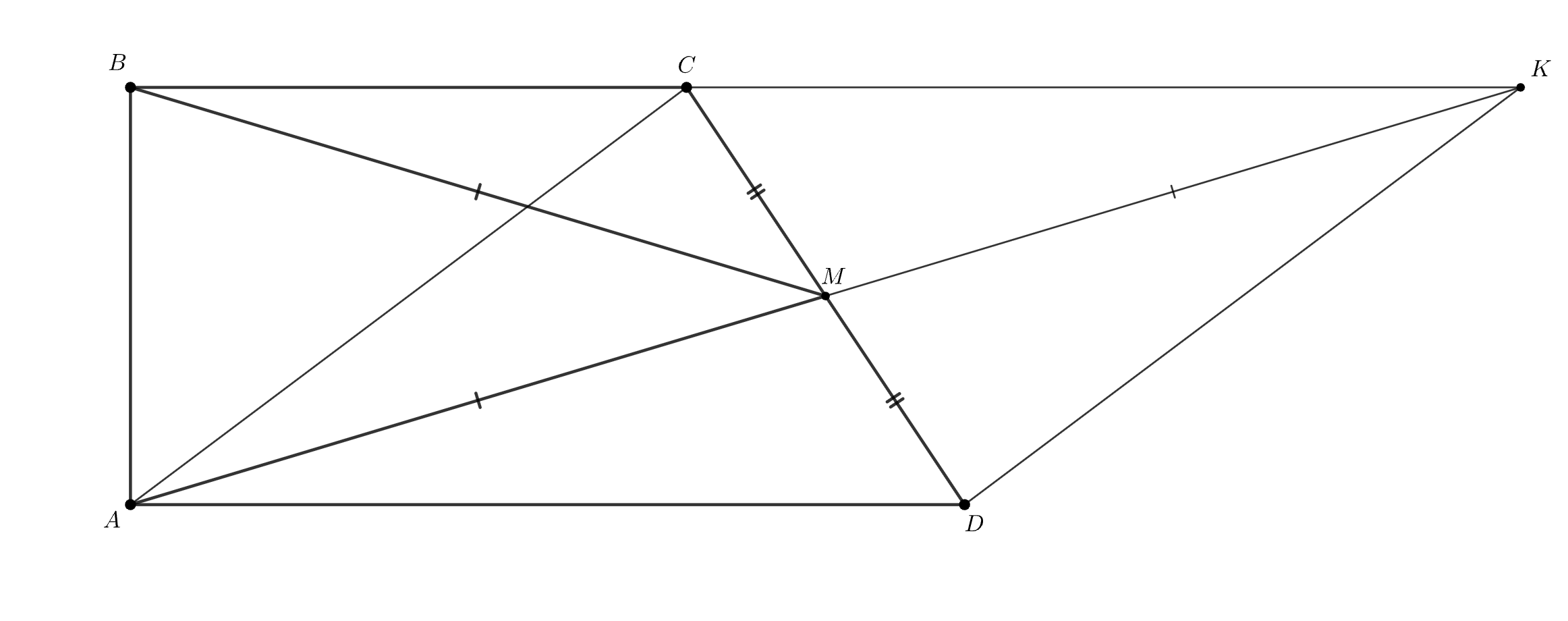
В трапеции основание
в четыре раза больше основания
а угол
в два раза больше угла
Найдите
отношение
где
— средняя линия трапеции.
Подсказка 1
Как можно воспользоваться условием на то, что один угол в два раза больше другого?
Подсказка 2
Проведем биссектрису CK угла BCD!
Подсказка 3
Чем является четырёхугольник BCKA?
Подсказка 4
BCKA — паралеллограмм! А что еще за собой повлекло проведение секущей CK?
Подсказка 5
Углы CKD и KCD равны! Тогда мы можем выразить почти все отрезки на рисунке через сторону BC ;)
Пусть основание равно
тогда из условия получаем, что
Зная оба основания, можем посчитать среднюю линию трапеции:
Пусть тогда по условию
Проведём биссектрису угла
которая пересекает
в точке
Тогда
По параллельности оснований трапеции Так как
то
а значит, четырёхугольник
— параллелограмм.
Тогда:
Осталось заметить, что треугольник равнобедренный, поэтому
Значит,
Ошибка.
Попробуйте повторить позже
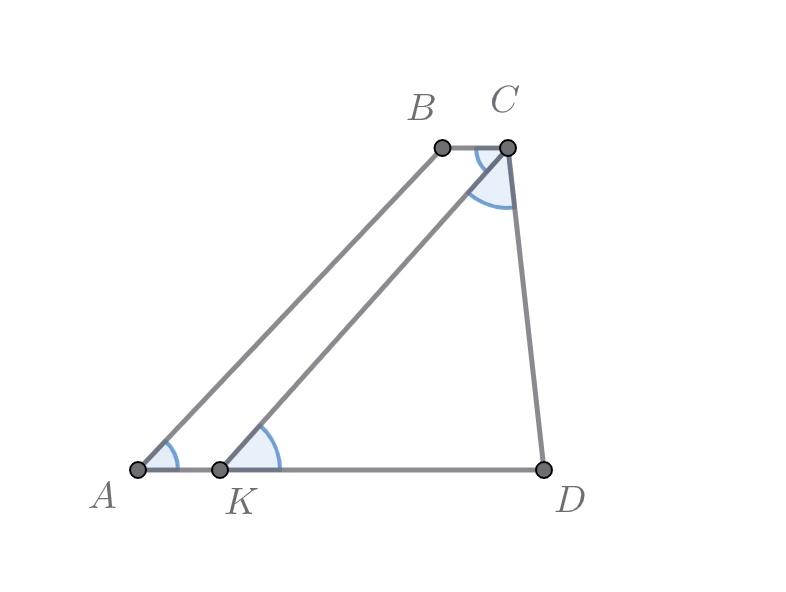
Даны лежащие в одной плоскости две трапеции и
с общим основанием
и одинаковыми высотами, равными
При этом
расстояние между точками
и
равно
Продолжения боковых сторон
и
пересекаются в точке
а сторон
и
— в точке
Найдите площадь четырехугольника
Источники:
Подсказка 1
Обратите внимание, что в этой задаче в рамках условия возможны разные рисунки. Отличие будет в расположении точек B, C, E, F.
Подсказка 2
В обоих случаях для решения достаточно вычислить длины высоты APQD и отрезка PQ. Обратите внимание, на рисунках большое количество подобных треугольников. Они в этом помогут.
Во-первых, заметим, что и точки
и точки
лежат по одну сторону от прямой
так как в противном случае
а
по условию
По обратной теореме Фалеса параллельна
Возможны две конфигурации:
1) Точки
расположены последовательно.
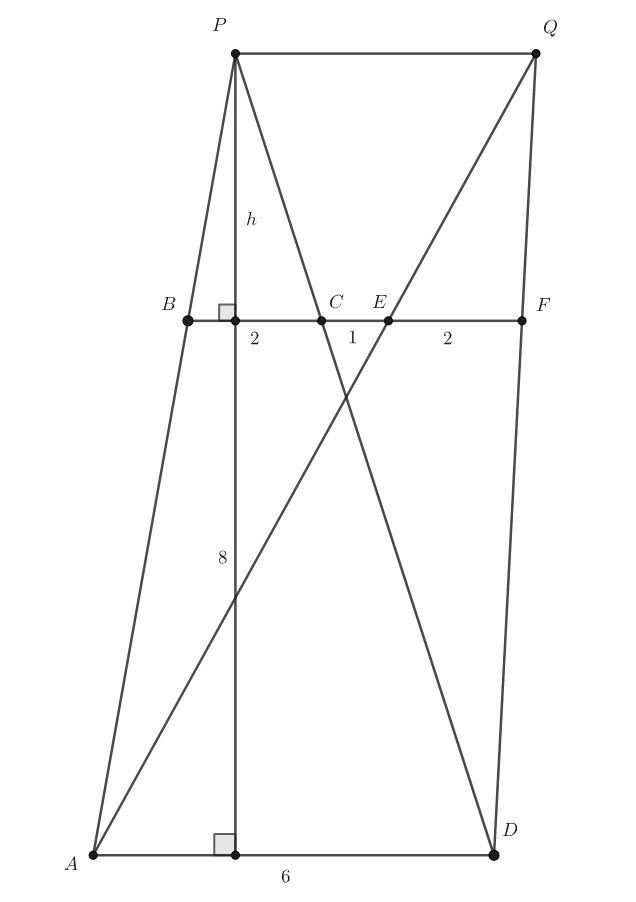
Если обозначить расстояние от точки до прямой
через
то из подобия треугольников
и
вытекает:
Отсюда Далее из подобия треугольников
и
:
Отсюда Тогда площадь трапеции
равна
2) Точка расположена между точками
и
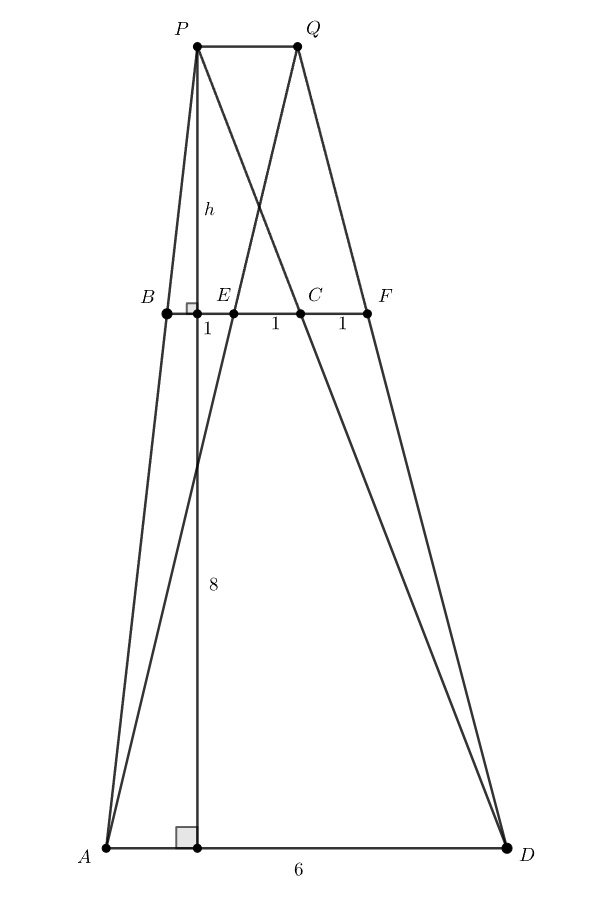
Аналогично:
Отсюда И из подобия треугольников
и
Отсюда Площадь трапеции
равна
или
Ошибка.
Попробуйте повторить позже
Углы при большем основании трапеции равны и
а меньшая боковая сторона равна
Найдите разность оснований.
Подсказка 1:
Попробуйте найти на рисунке отрезок, равный разности оснований.
Подсказка 2:
Чтобы это сделать, нужно на большем основании с одного из концов отметить отрезок, равный меньшему основанию. Тогда оставшаяся часть будет разностью. Как это сделать?
Подсказка 3:
Можно сделать параллельный перенос отрезка BC на прямую AD так, чтобы точка B перешла в точку A. На какой вектор надо перенести, чтобы так получилось?
Пусть и
— основания трапеции
причем
Через вершину проведем прямую, параллельную боковой стороне
Пусть эта прямая пересекает основание
в точке
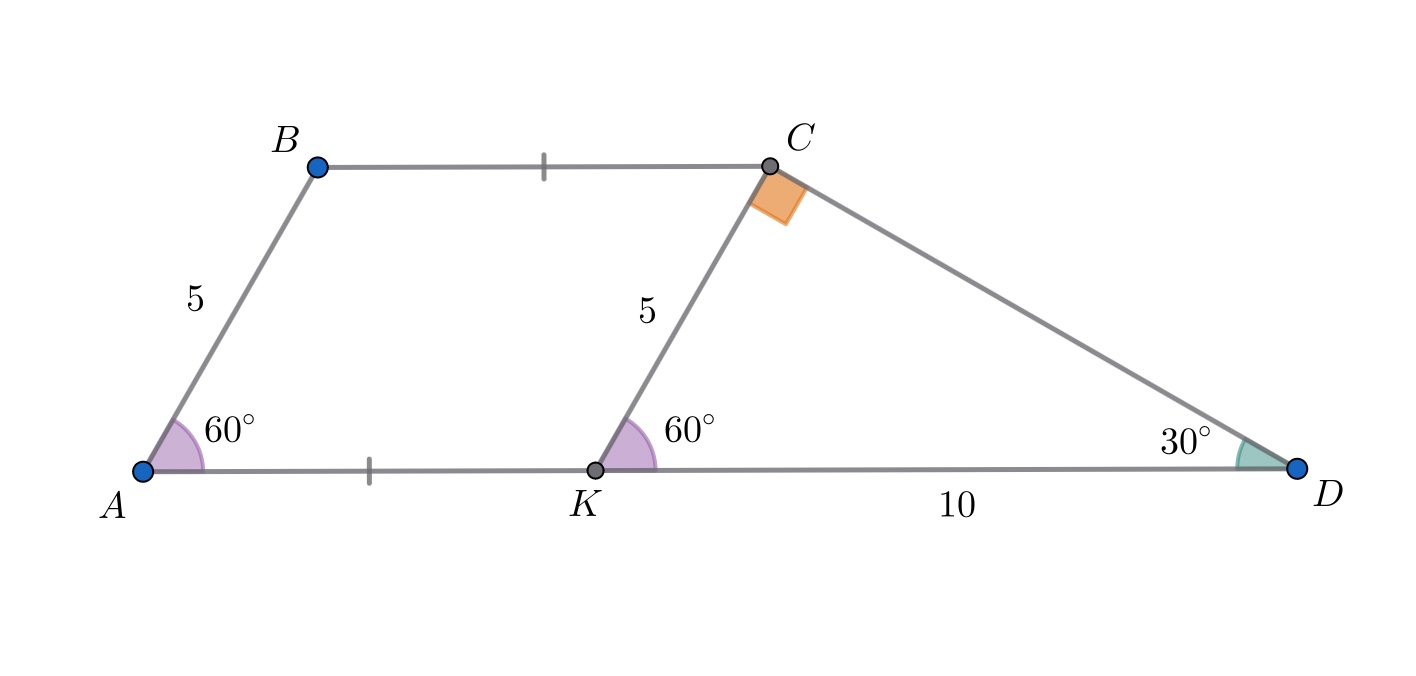
Тогда — параллелограмм. Поэтому получаем следующие равенства отрезков:
Из равенства соответственных углов получаем:
В прямоугольном треугольнике катет
лежит против угла в
следовательно,
Ошибка.
Попробуйте повторить позже
В прямоугольной трапеции меньшая диагональ равна большей боковой стороне. Найдите большую диагональ, если большая боковая сторона
равна а меньшее основание равно
Пусть — большая боковая сторона трапеции
— меньшее основание,
— большая диагональ.
Опустим перпендикуляр
на большее основание
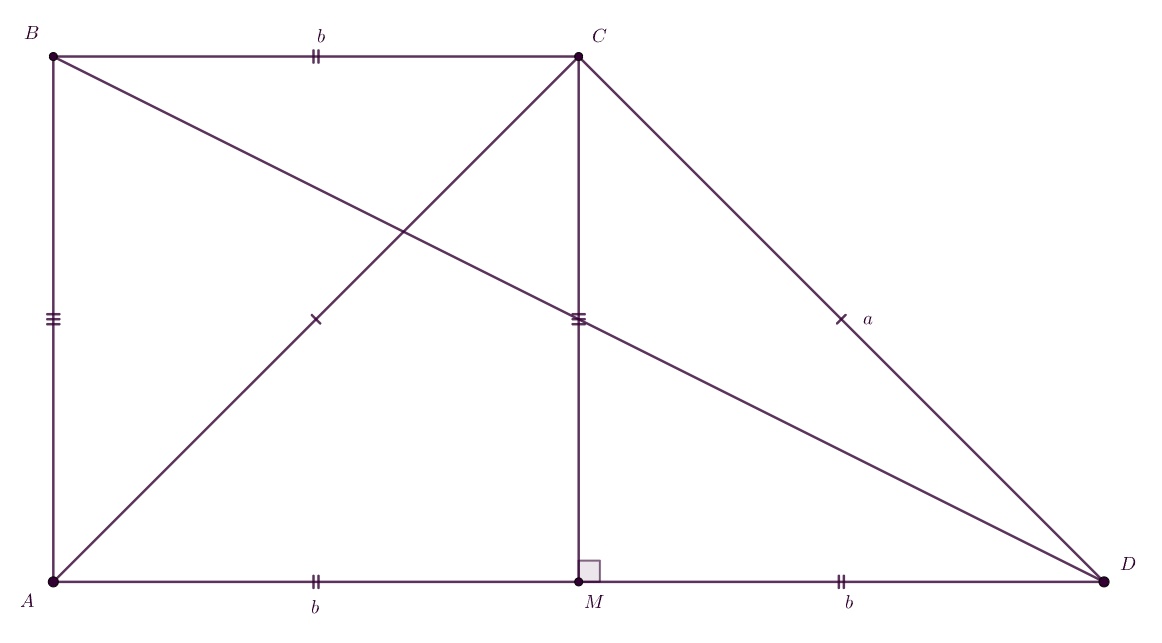
Поскольку то
а так как
то
Значит,
Следовательно,
Ошибка.
Попробуйте повторить позже
Дана трапеция Известно, что
а биссектрисы углов
и
пересекаются в точке
лежащей внутри
трапеции. Докажите, что описанные окружности треугольников
и
касаются.
Источники:
Подсказка 1:
В данном случае для доказательства касания достаточно показать, что окружности имеют общую точку, лежащую на их линии центров. Подумайте, почему это так.
Подсказка 2:
Значит, нужно понять, какая прямая является их линией центров. Для этого нужно узнать какую-то дополнительную информацию про окружности. Обратите внимание на треугольник CED.
Подсказка 3:
Биссектрисы односторонних углов пересекаются под прямым углом, поэтому треугольник CED прямоугольный. А что можно сказать про прямую, содержащую его медиану, проведённую к гипотенузе?
Подсказка 4:
Чтобы она стала линией центров этих окружностей, она должна стать средней линией трапеции. Действительно, она же тогда будет проходить через середины боковых сторон.
По условию и
, поэтому
— основания трапеции. Пусть
и
— середины
и
так что
—
средняя линия трапеции
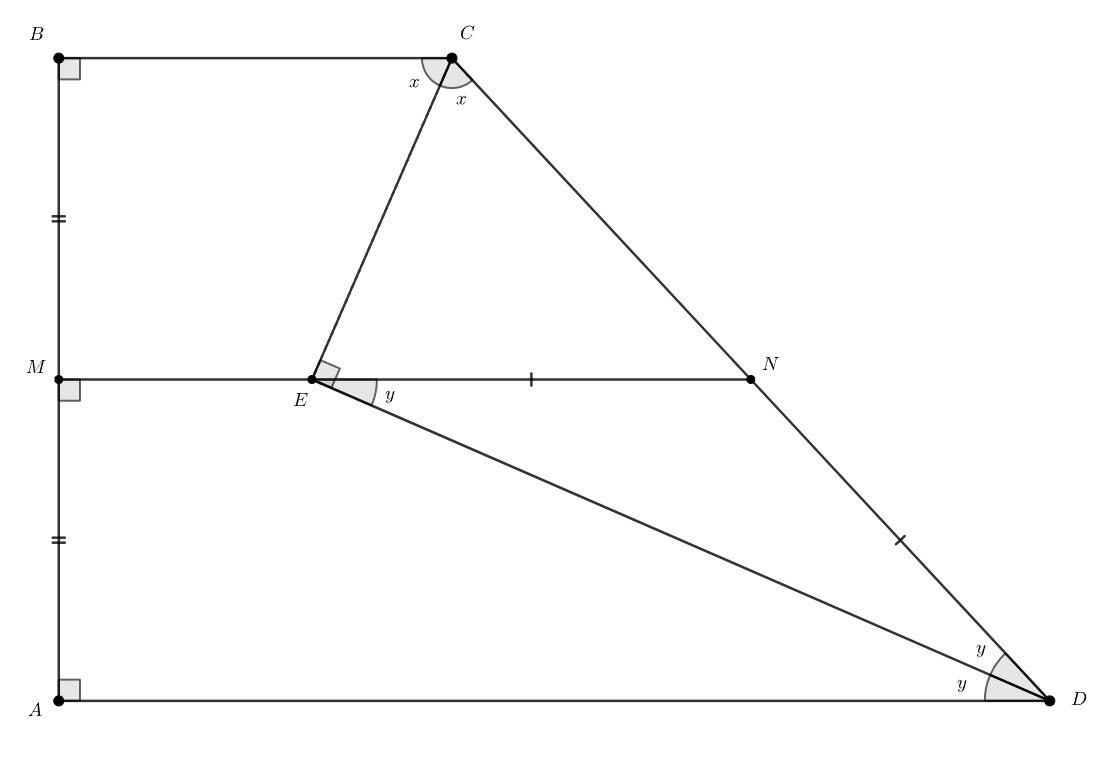
При этом параллельна основаниям, поэтому
и значит,
— серединный перпендикуляр к
Значит, центр
окружности
лежит на прямой
Положим
Из параллельности следует, что
, поэтому
.
Видим, что треугольник — прямоугольный (
), а значит,
— центр окружности
Далее, в прямоугольном треугольнике имеем
поэтому
, а из равенства углов
следует
поэтому
лежит на прямой
Итак, — общая точка окружностей
и
лежащая на их линии центров
Значит, эти окружности касаются (в
точке
).
Ошибка.
Попробуйте повторить позже
Середина основания трапеции равноудалена от концов другого основания. Обязательно ли данная трапеция равнобокая?
Пусть — середина основания
трапеции
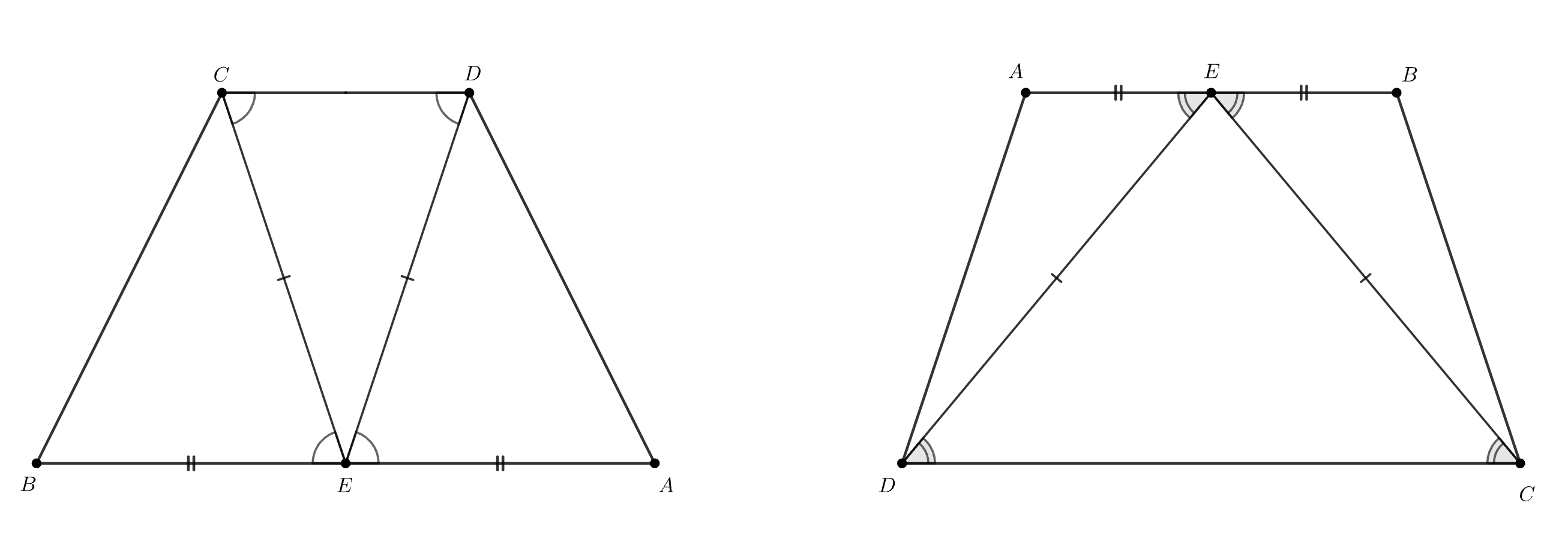
Треугольник — равнобедренный, следовательно
. Основания трапеции параллельны, поэтому
и
Значит по двум сторонам и углу между ними. Поэтому
то есть трапеция равнобокая.
Да, обязательно
Ошибка.
Попробуйте повторить позже
Середина боковой стороны трапеции равноудалена от двух противоположных от неё вершин. Докажите, что трапеция прямоугольная.
Пусть точка — середина боковой стороны
трапеции
По условию,
Продлим отрезок
на его длину за
точку
получим отрезок
Так как
то
— параллелограмм.
следовательно, точка
лежит на прямой
В
треугольнике
другими словами, медиана равна половине стороны, к которой проведена, следовательно,
треугольник является прямоугольным, тогда
Ошибка.
Попробуйте повторить позже
Произвольную точку внутри равностороннего треугольника
соединили с вершинами. Докажите, что на каждой стороне
треугольника можно выбрать по одной точке так, чтобы расстояния между ними были равны
и
.
Проведем
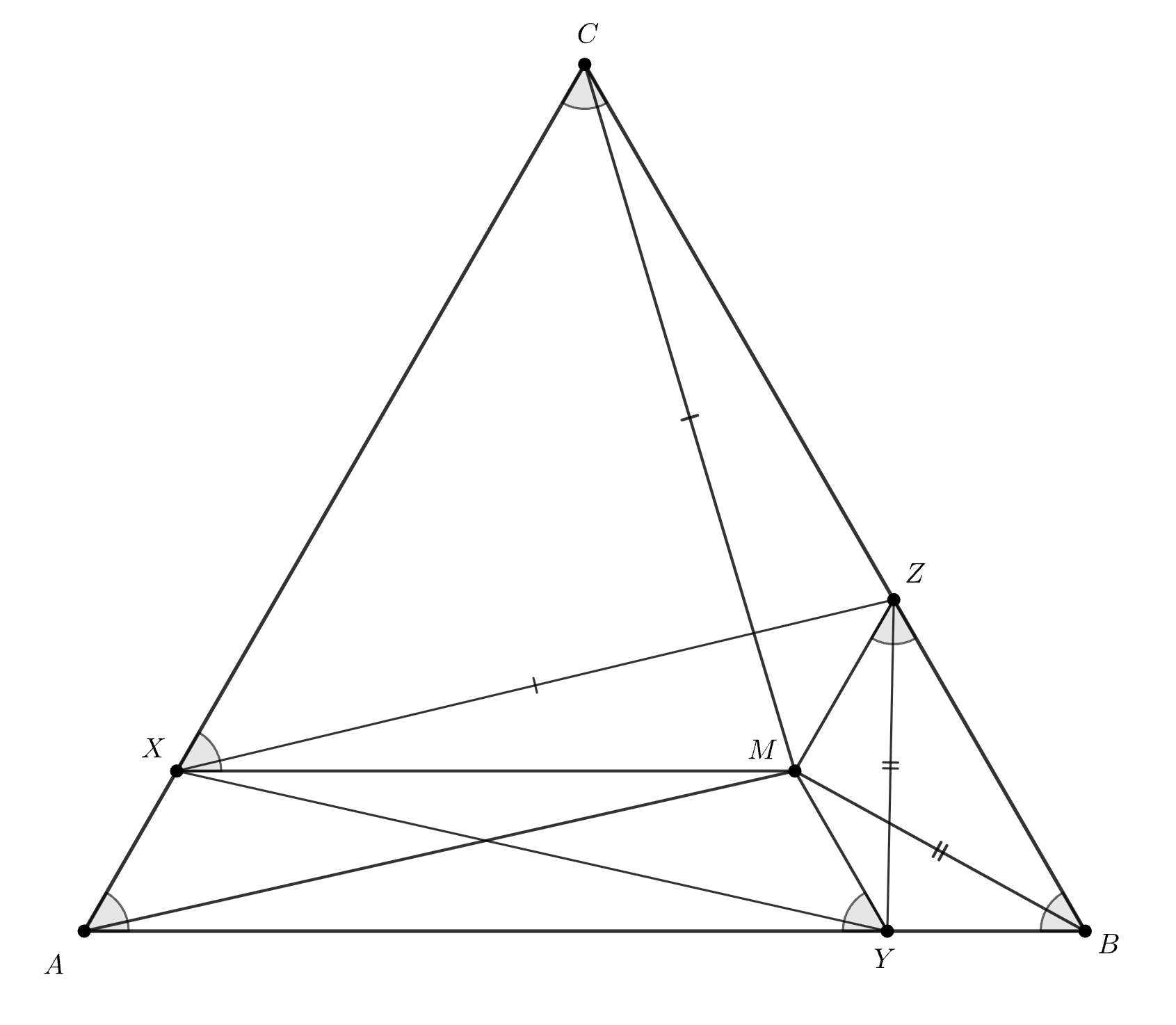
По построению,
Заметим, что трапеции
и
— равнобедренные. Так как в равнобедренной трапеции диагонали равны,
—
искомый.
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и
Боковая сторона
равная
перпендикулярна основаниям. На
сторонах
и
взяты соответственно точки
и
такие, что
Найдите все углы треугольника
Источники:
Подсказка 1
Нам дана очень хорошая трапеция, давайте найдём ее углы и попробуем понять что-то хорошее о четырёхугольнике АMCN.
Подсказка 2
Он вписанный! Так как сумма углов MCN и MAN равна 180º. Попробуем найти угол AMN, может на рисунке есть угол, равный ему?
Подсказка 3
Вписанные углы AMN и ACN опираются на одну и ту же дугу, а значит, они равны! А как найти угол ACN? Обратите внимание на равные отрезки, они помогут определить угол ВСА, а зная его, мы легко можем найти ACN, а значит, и все углы треугольника AMN)
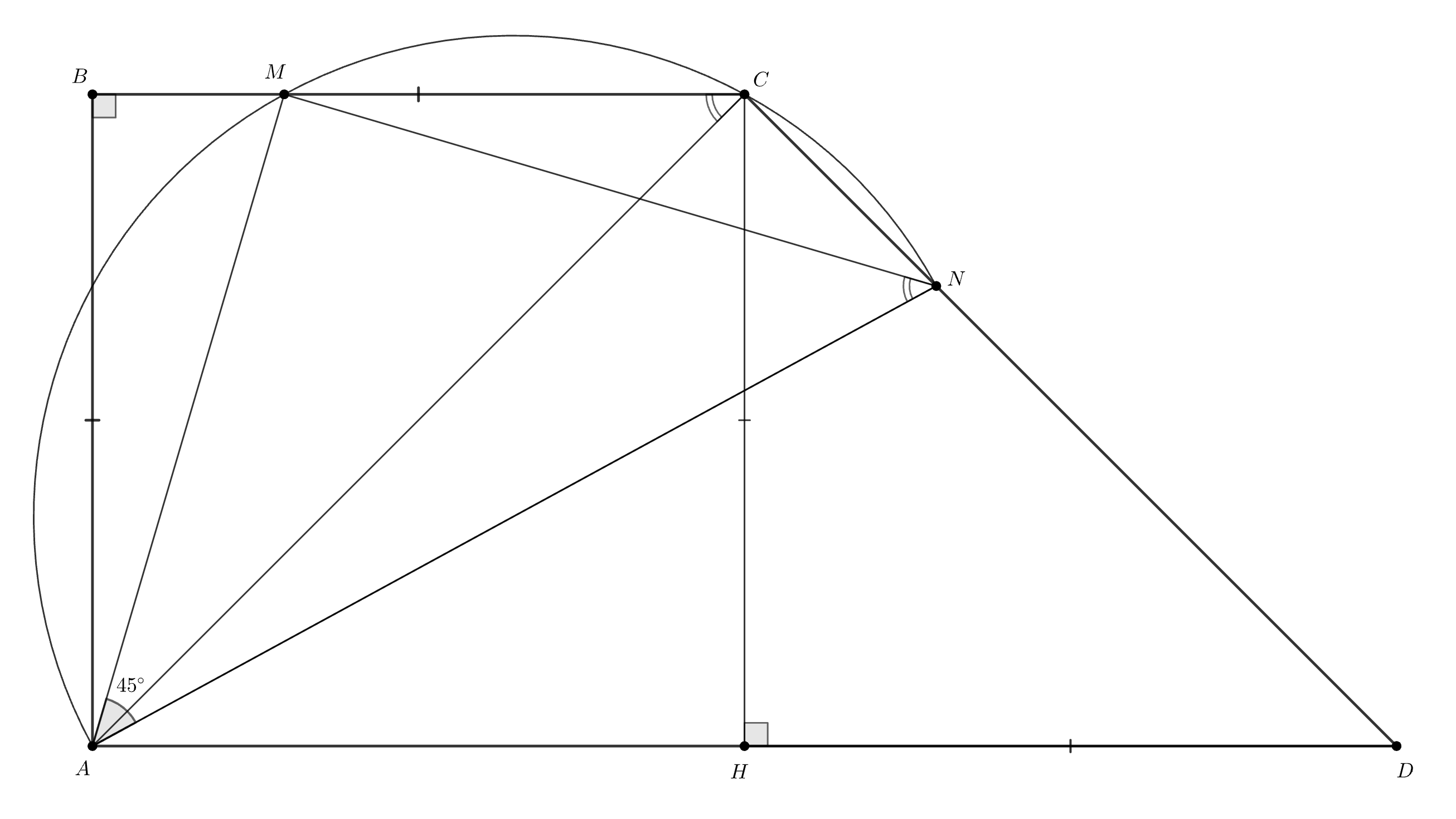
Поскольку и
получаем, что
Проведем высоту
Она будет равна
так как
тогда
Кроме того,
По условию,
так как
четырехугольник
является вписанным.
как вписанные углы, опирающиеся на одну
дугу.
Ошибка.
Попробуйте повторить позже
В трапеции оказалось, что
и
Найдите угол
Источники:
Подсказка 1
Сделаем рисунок. Пока не очень понятно, откуда на картинке возьмётся нужное, да и условие про сумму длин двух сторон явного результата не даёт. Значит, надо придумать дополнительные построения! Какие распространённые конструкции Вы знаете?
Подсказка 2
Хочется, чтобы у нас появился ещё один (или не один) отрезок, равный AB + CD. Для этого можно провести прямые через середину боковой стороны BC и оставшиеся вершины трапеции. Что интересного можно сказать о треугольниках, полученных в результате пересечения проведённых прямых с прямыми, содержащими основания трапеции?
Подсказка 3
Итак, у нас образовался четырёхугольник с тремя равными и двумя параллельными сторонами. Это ...?
Подсказка 4
Докажите, что это параллелограмм. Подумайте, в каком параллелограмме могут быть равны 3 стороны.
Подсказка 5
Тут уже неплохо считаются многие углы, но чего-то всё равно не хватает. Попробуем добавить в конструкцию ещё равнобедренных треугольников, а может и более "интересных", например, ... . Отразите точку B относительно диагонали ромба.
Подсказка 6
Осталось лишь увидеть тот самый равносторонний треугольник, ещё немного поработать с углами и симметрией и наслаждаться победой!
Отметим середину стороны точку
Продлим луч
до пересечения с прямой
в точке
и луч
до пересечения с
прямой
в точке
Из равенства треугольников и
получаем, что
Откуда — равнобедренный треугольник. Аналогично равны треугольники
и
откуда равнобедренным является
треугольник
Получаем, что четырёхугольник
является ромбом.
Отразим точку относительно диагонали
получим точку
Так как
То и
Получаем, что в равнобедренном треугольнике
угол
равен
значит, треугольник
равносторонний.
Треугольник равнобедренный, поэтому
то есть трапеция
равнобедренная. Из этого получаем,
что
То есть
В силу симметрии в ромбе
Ошибка.
Попробуйте повторить позже
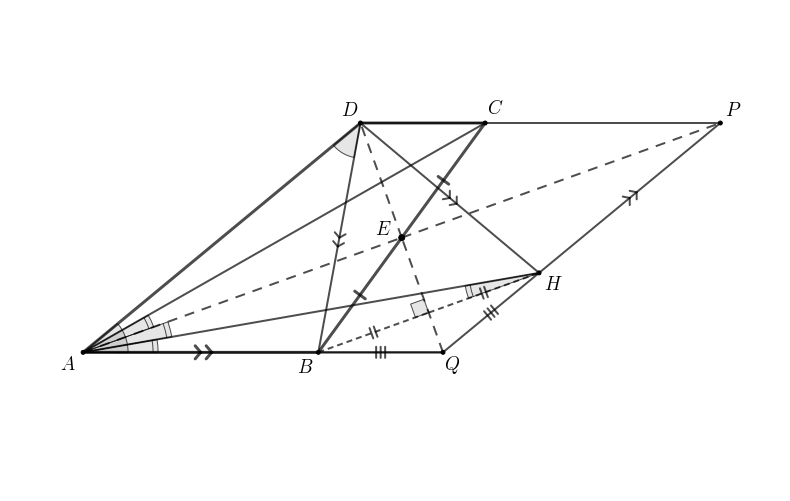
В трапеции углы
и
при основании
соответственно равны
и
Точка
лежит на основании
причём
Точка
лежит на основании
прямая
параллельна боковой стороне
и делит площадь трапеции
пополам. Найдите
Пусть
Тогда
Так как
— параллелограмм, то
Проведем высоту
Получим,
что
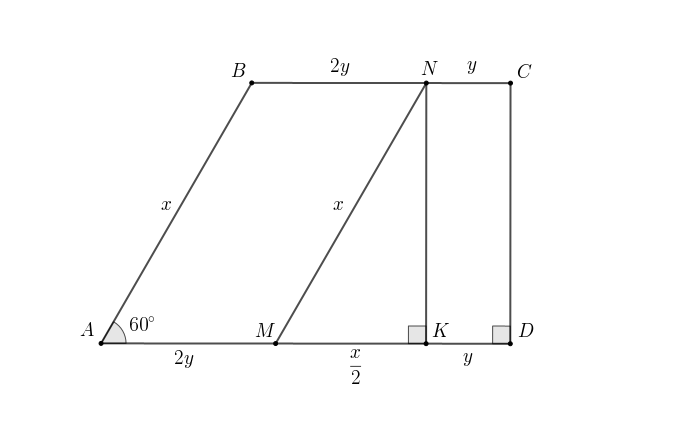
По условию, площадь параллелограмма равна площади трапеции
Поскольку
является для них высотой, верно,
что
Тогда
Ошибка.
Попробуйте повторить позже
В трапеции сумма углов при одном из оснований равна Найдите длину отрезка, соединяющего середины оснований, если длина
отрезка, соединяющего середины диагоналей, равна
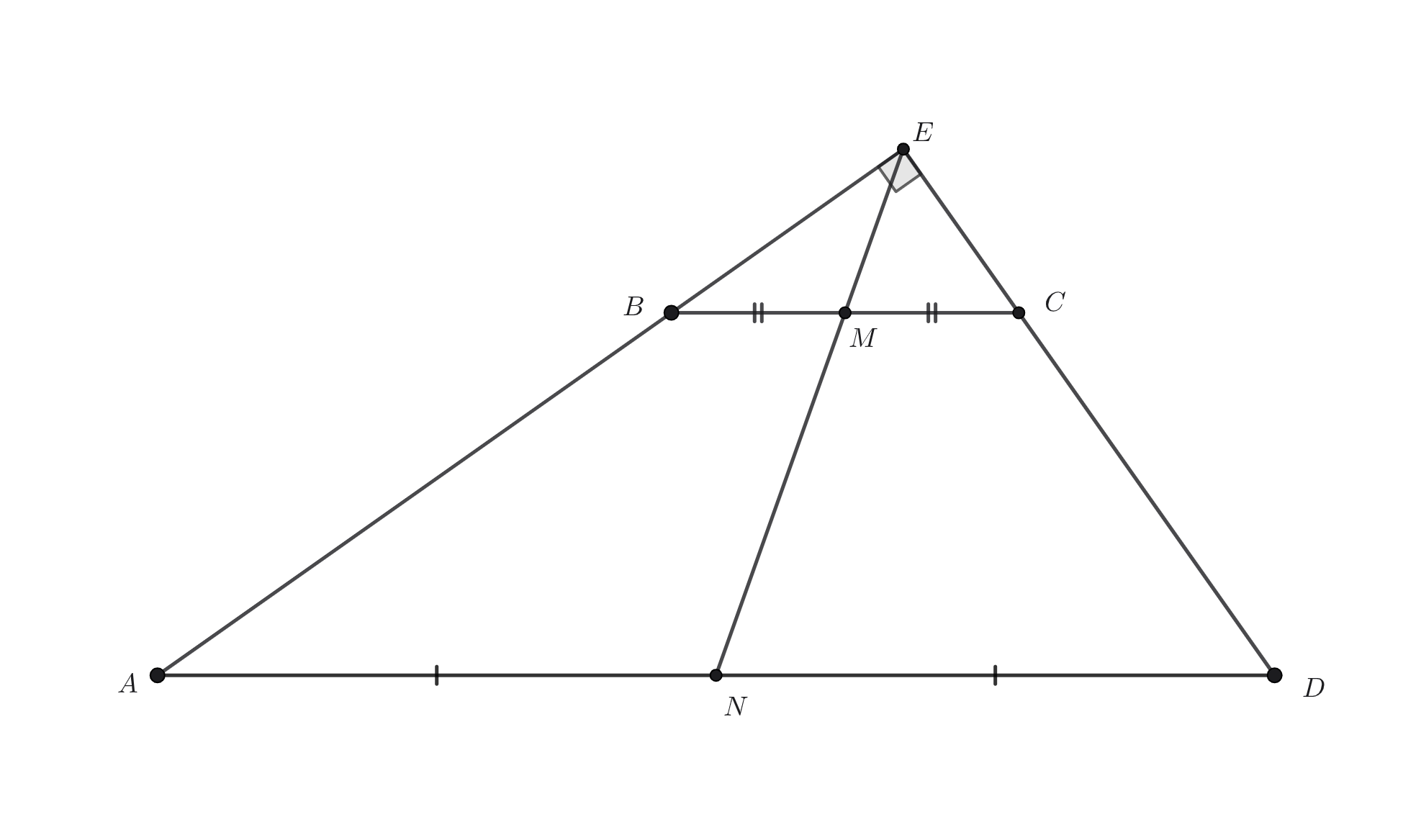
Продлим боковые стороны трапеции до пересечения. Пусть пересекает
в точке
По условию
откуда
Пусть а точки
и
— середины сторон
и
соответственно. Отсюда
— медиана прямоугольного
треугольника
По свойству прямоугольного треугольника
Получается, треугольник
— равнобедренный, то
есть
Аналогично,
— медиана прямоугольного треугольника
откуда
то есть треугольник
— равнобедренный и
Заметим, что
как соответственные углы при параллельных прямых
и
и секущей
Отсюда
Так как то точки
лежат на одной прямой, откуда
Получается, искомый отрезок, соединяющий середины оснований нашей трапеции, равен полуразности оснований. С другой стороны, мы
знаем, что длина отрезка, соединяющего середины диагоналей трапеции, так же равна полуразности оснований. По условию длина этого
отрезка равна отсюда искомая длина так же равна
Ошибка.
Попробуйте повторить позже
В трапеции
Докажите, что
Первое решение.
В силу параллельности
Отложим от точки отрезок
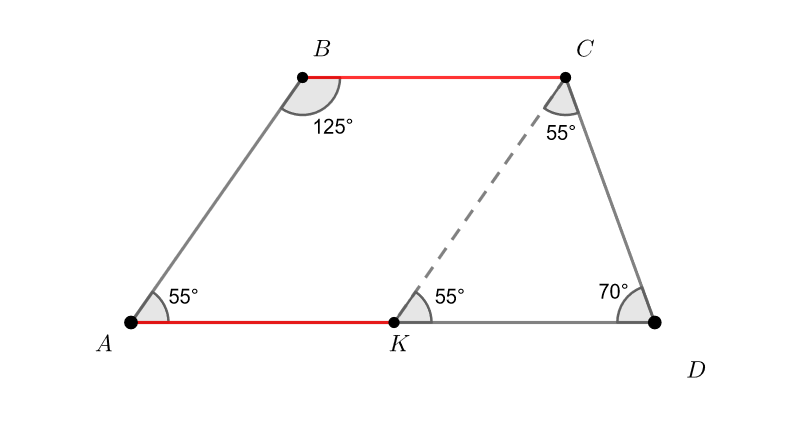
Тогда — параллелограмм (т. к.
а
Значит, как односторонние углы при секущей
Найдем угол
Получили, что Тогда
— равнобедренный, в котором
В итоге,
______________________________________________________________________________________________________________________________________________________
Второе решение.
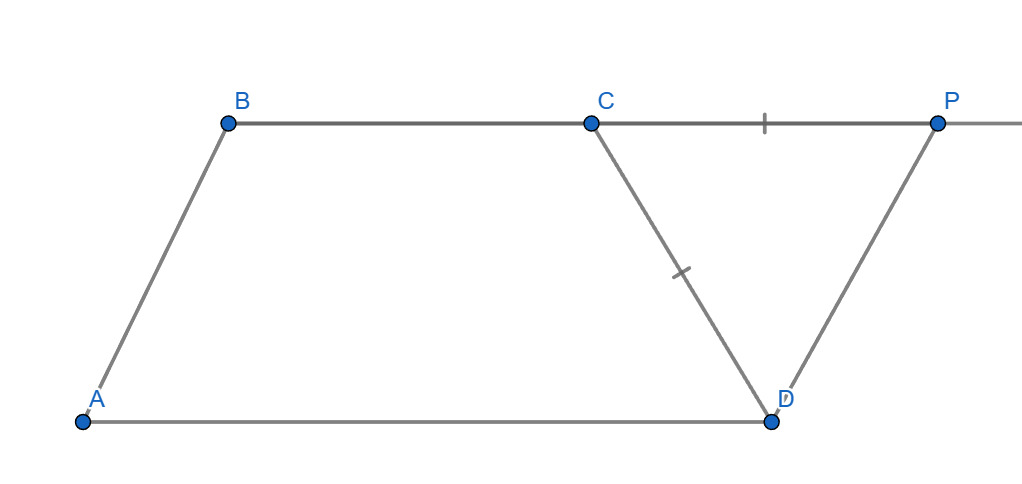
Отложим на прямой за точку
отрезок
равный
Т.к. можем получить
Треугольник равнобедренный, т.к.
поэтому
Получаем, что
Следовательно, значит,
Но мы знаем, что
поэтому
— параллелограмм.
Значит,
Ошибка.
Попробуйте повторить позже
Основания трапеции равны и
Найдите отрезок, соединяющий середины оснований, если диагонали трапеции перпендикулярны.
Подсказка 1
Как воспользоваться условием на диагонали трапеции для решения задачи? Определите расположение точки пересечения диагоналей O относительно отрезка, соединяющего середины оснований E и F.
Подсказка 2
Точка O будет лежать на отрезке EF! И этот факт всегда выполняется в трапеции! Докажите это воспользовавшись подобием треугольников. После этого длину EF можно будет вычислить, как сумму EO + OF.
Подсказка 3
Если E, F --- середины оснований трапеции BC, AD, то докажите подобие треугольников BOC и AOD, после чего докажите подобие BOE и DOF. Тогда равны углы BOE = DOF и O лежит на EF. Легко теперь найти EO, OF --- медианы к основаниям в прямоугольных треугольниках BOC, AOD.
Пусть нам дана трапеция (
— ее основания). Точки
— середины оснований
и
соответственно,
— точка
пересечения диагоналей трапеции. Докажем, что
лежит на отрезке
.
![]()
Треугольники подобны по двум углам. Тогда:
Но
Значит, в силу равенства
и отношению сторон:
Из подобия получаем равенство углов , что говорит о том, что
лежат на одной прямой.
Диагонали трапеции перпендикулярны, поэтому прямоугольные. В прямоугольных треугольниках медиана к гипотенузе
равны ее половине, то есть
Ошибка.
Попробуйте повторить позже
В трапеции основание
в два раза меньше основания
Из вершины
опущен перпендикуляр
на сторону
Докажите, что
Подсказка 1
Какие бывают способы доказать равенство сторон? Самый очевидный - найти их длины. Менее очевидный - доказать равнобедренность треугольника через то, что в нем медиана, высота и биссектриса к основанию совпадают. Вычислять длины CE, CD, сложно, поэтому попробуйте применить второй подход. Еще полезно поразмышлять, как использовать условие, что длина BC в 2 раза меньше длины AD. Может попытаться получить равные отрезки?
Подсказка 2
Пусть O - середина отрезка ED. В какой тогда точке должна пересекать прямая CO основание AD, чтобы ECD был равнобедренным?
Подсказка 3
Чтобы ECD был равнобедренным, CO должна быть медианой и высотой. Но тогда прямая CO будет содержать среднюю линию треугольника AED, то есть пересечет AD в середине. Осталось понять, почему это будет правдой?
Пусть — середина основания
По условию основание
в два раза меньше
то есть:
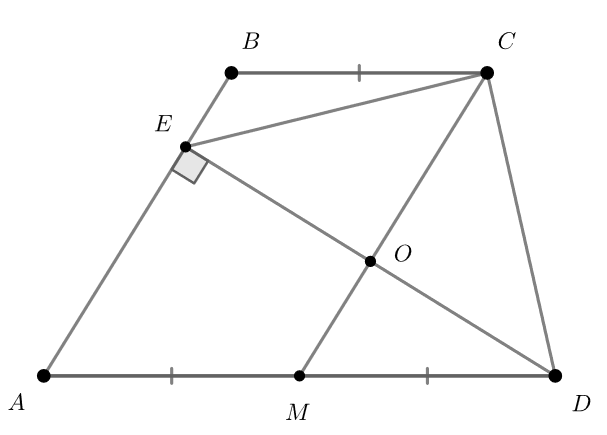
Тогда — параллелограмм, потому что стороны
равны и параллельны. Следовательно, будут параллельны
Так
как
— высота к
получаем
При этом — прямая, содержащая среднюю линию в треугольнике
так как параллельна
и проходит через середину
Следовательно,
проходит через точку
— середину
В итоге, — высота и медиана треугольника
Значит, он равнобедренный и
Ошибка.
Попробуйте повторить позже
В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
Пусть дана трапеция
— отрезок, соединяющий середины оснований
и
— точка пересечения диагоналей
и
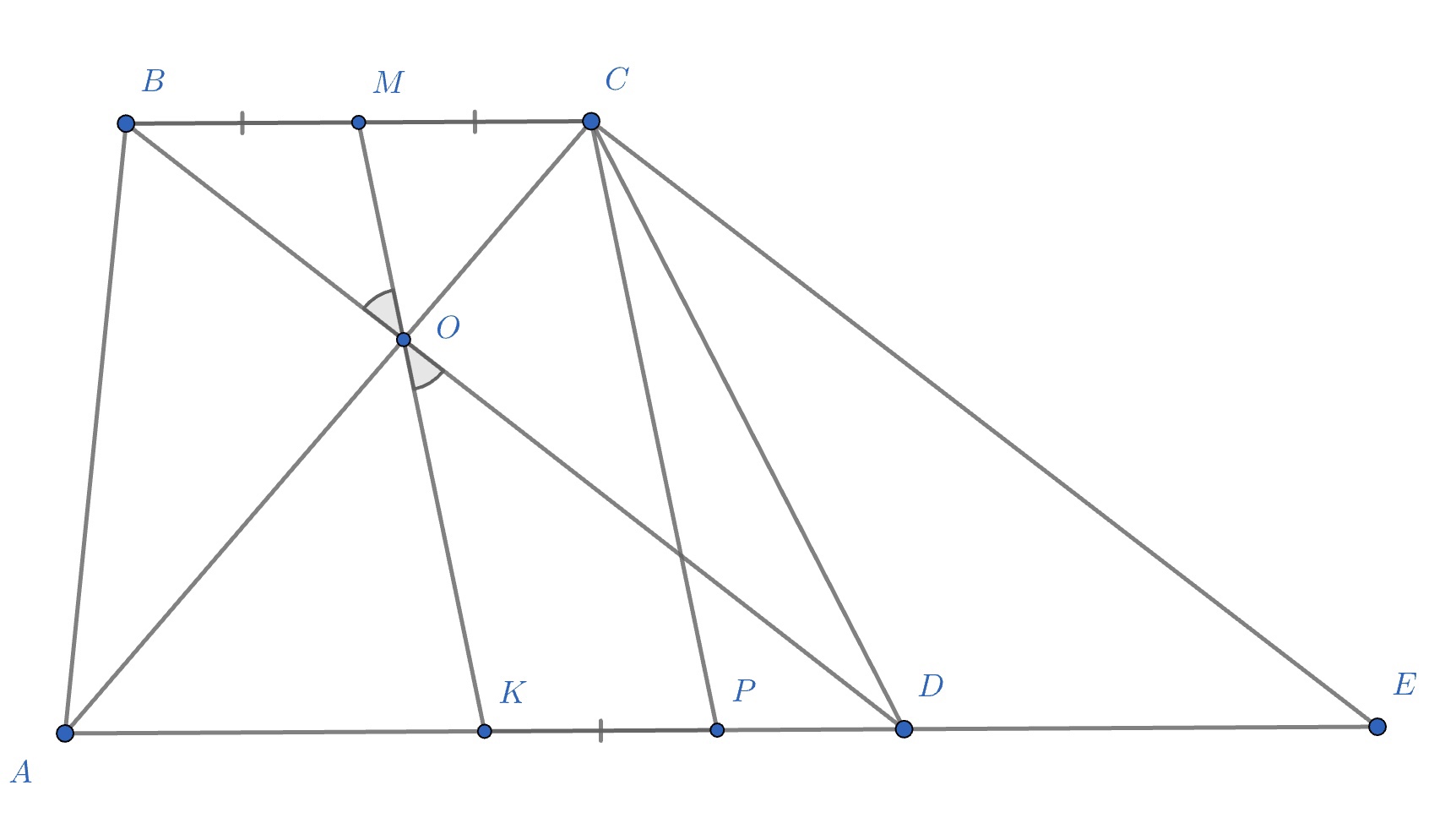
Тогда, так как треугольники
и
подобны.
и
— соответствующие элементы в подобных
треугольниках (медианы). Значит,
Следовательно, точки
и
лежат на одной прямой.
Проведём где точка
лежит на продолжении стороны
Тогда, так как
и
—
параллелограмм.
Так как диагональ в параллелограмме делит его на равных треугольника,
Заметим, что так как они имеют общее основание
а вершины
и
лежат на прямой, параллельной
основанию
(что означает, что их высоты из точки
будут равны). Получаем:
Значит,
Таким образом, нам нужно найти площадь у которого известны
стороны:
по условию,
так как
— параллелограмм.
Проведём лежит на
Тогда, так как
и
— параллелограмм. Значит,
Таким образом, значит,
— медиана
Получается, в
нам также известна медиана:
Сделаем выносной чертёж
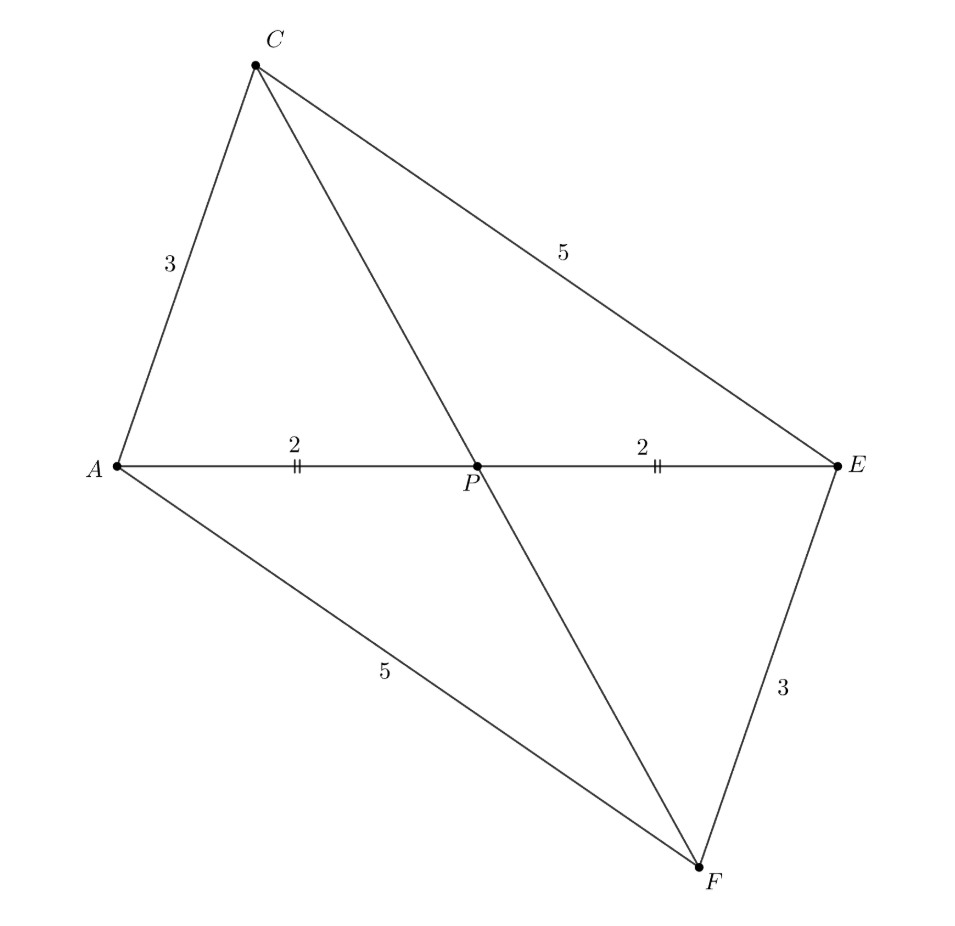
Продлим медиану на свою длину — точка
Тогда, четырёхугольник
— параллелограмм (диагонали точкой пересечения
делятся пополам). Значит,
Заметим, что так как
Значит, нам нужно найти площадь
Так как его стороны
равны
то по обратной теореме Пифагора этот треугольник прямоугольный. Значит, его площадь
равна
Тогда,
6
Ошибка.
Попробуйте повторить позже
В трапеции диагонали пересекаются в точке
Прямая, проведенная через точку
параллельная
пересекает
в
точке
Известно, что
а
Найдите длину
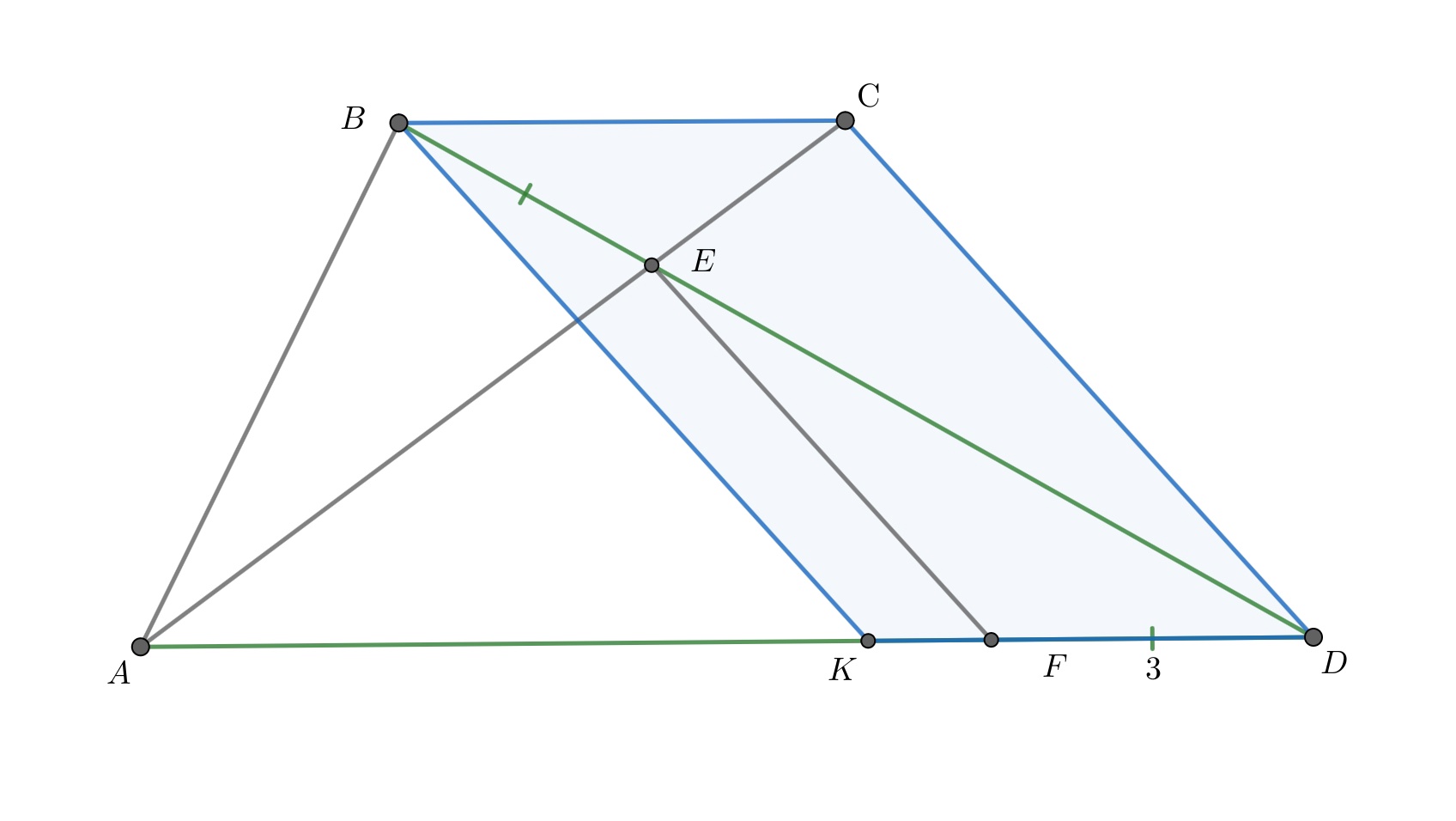
Поскольку треугольники
и
подобны, и потому
Достроим треугольник до параллелограмма
Тогда треугольник
и
подобны, поэтому
Наконец, поскольку и
получаем
Отсюда следует, что
Ошибка.
Попробуйте повторить позже
В трапеции длины диагонали
и основания
равны. Точка
на луче
такова, что
На прямой
взята точка
такая, что
Известно, что
(При этом
и
Найдите
градусную меру угла
Источники:
Подсказка 1
Множество равных отрезков да еще и параллельные прямые в трапеции. В такой картинке больше всего хочется найти все равные углы, которые есть, давайте так и поступим.
Подсказка 2
Если вы правильно воспользуетесь равнобедренными треугольниками и параллельностью AD и BC, то станет понятно, что ∠XCB = ∠XDA. Еще мы знаем, что BD = BC, то есть точки D и C находятся как бы на одной окружности с центром в точке B. Что хочется сделать в такой конструкции?
Подсказка 3
Давайте повернем рисунок против часовой стрелки относительно точки B на угол равный альфа. Куда в таком случае перешли точка C и прямая CX?
Подсказка 4
Точка C перейдет в точку D, а прямая CX в прямую AD. Вспомните, что BA=BY, и подумайте, куда в таком случае могла перейти точка Y. Рассмотрите все возможные случаи и найдите в каждом случае градусную меру угла ∠BYC
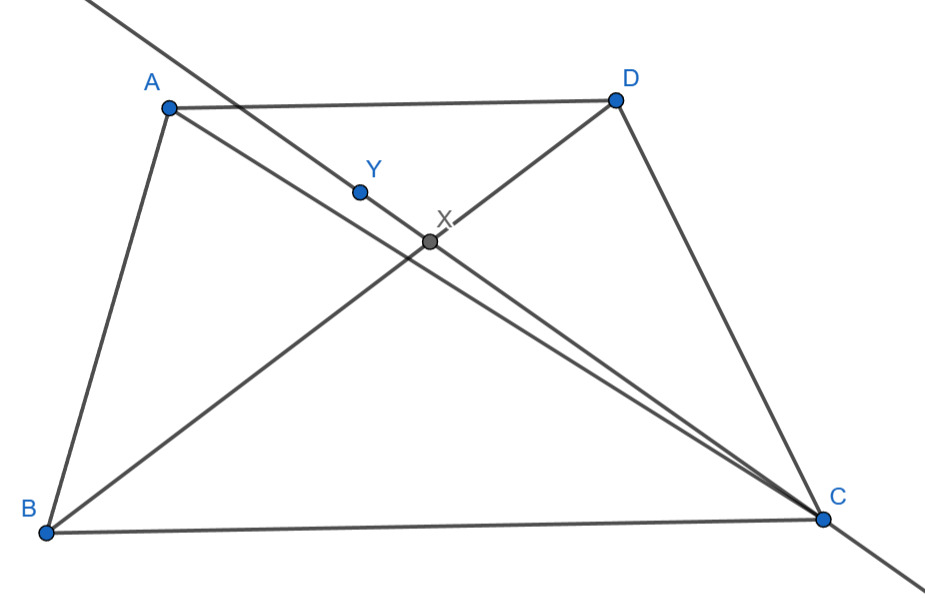
равнобедренный, поэтому
Накрест лежащие углы равны:
. Значит,
Повернём картинку на угол относительно точки
так, чтобы точка
перешла в точку
Из доказанного выше равенства углов
следует, что прямая
при этом повороте перейдёт в прямую
Точка
при этом перейдёт в такую точку на прямой
что расстояние от неё до точки
равно
Таких точек две. Одна из них точка
а вторая — какая-то точка
Значит, или
как односторонний угол. Это один из
ответов.
Посмотрим теперь на точку
равнобедренный, причём
равен тому из углов
и
который
является острым (случай прямого угла исключается значениями углов
и
которые даны в каждом их вариантов).
Если
тупой, точка
очевидно лежит на луче
и
Если же
острый,
и точка
находится на луче
При этом во всех вариантах
т.е.
поэтому точка
лежит ближе к
чем
, т.е. попадает на отрезок
Значит,
Ошибка.
Попробуйте повторить позже
На боковой стороне трапеции
нашлась точка
такая, что
Пусть прямые
и
пересекаются в точке
а прямые
и
— в точке
Докажите, что углы
и
равны.
Подсказка 1
Что хочется провести, что начать записывать цепочку равенств углов, начиная с DAM? На картинке много параллельностей, есть смысл обращаться к углам с помощью отрезков!
Пусть — точка пересечения прямых
и
точка
— точка пересечения прямых
и
Из параллельности прямых
и
следует равенство углов
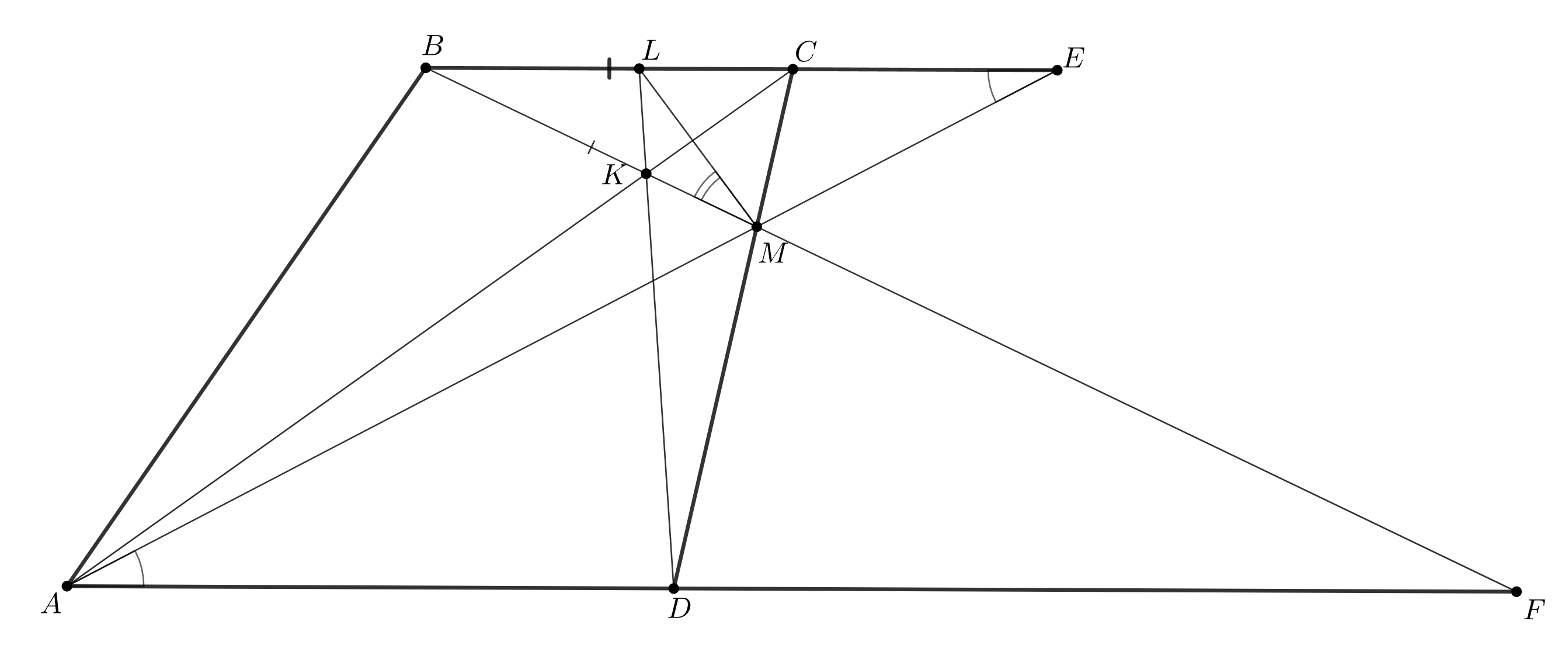
Достаточно показать, что что эквивалентно тому, что прямая
касается окружности
, то есть тому, что
верно равенство произведений отрезков секущих
а в силу
, равенство
Осталось заметить, что, в силу подобия треугольников и
а в силу подобия треугольников и
Получаем
Домножив обе части равенства на произведение знаменателей, получим требуемое.



