Трапеция
Ошибка.
Попробуйте повторить позже
В трапеции угол
равен
, угол
равен
. Боковая сторона
вдвое меньше основания
. Чему может равняться
угол
?
Подсказка 1
Раз уж CD — это половина AD, давайте отметим середину AD (точка E). Что можно сказать про треугольник CDE?
Подсказка 2
Отлично, треугольник CDE — равнобедренный! А ещё в нем известен один угол) Давайте найдем два остальных.
Подсказка 3
Итак, углы треугольника CDE равны 43, 43, 94. Давайте теперь внимательно посмотрим на условие) Что нам даёт такое равенство углов?
Подсказка 4
AB и EC параллельны! А что можно тогда сказать про четырехугольник AECB?
Подсказка 5
AECB — параллелограмм! А что тогда можно сказать про BC?
Подсказка 6
BC = AE = CD! Отлично, значит, у нас появился ещё один равнобедренный треугольник, в котором мы можем посчитать угол) Осталось понять чему равен угол BCD.
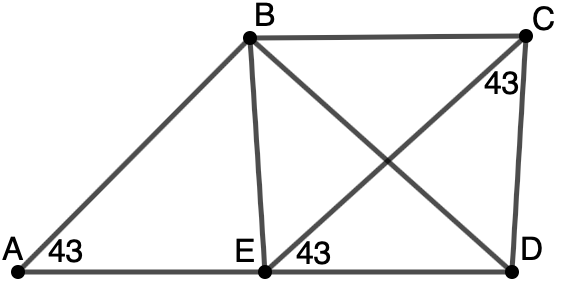
Пусть — середина
. Рассмотрим треугольник
. По условию
. Отсюда видно, что этот треугольник
равнобедренный.
, тогда
.
— параллелограмм, так как
,
, потому
что
— соответственные при параллельных прямых. Тогда
, но в то же время
, значит,
треугольник
— равнобедренный с углом
. Поймем, что
, тогда
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




