Степень точки и радикальные оси

Пусть отношение радиусов — середина и — центры гомотетий с положительным и отрицательным коэффициентами, переводящих в

Покажем, что вторично пересекает линию центров в точке Если радиусы окружностей равны, то касается линии центров в точке Иначе и — внутренняя и внешняя биссектрисы треугольника поскольку

и, аналогично, Из прямоугольного треугольника тогда

Точки и — центры гомотетий с положительными коэффициентами, переводящих в и По теореме о трех гомотетиях и лежат на одной прямой. Далее, пусть и пересекают вторично соответственно в и Пользуясь гомотетией и степенью точки, получаем

Теперь имеем , значит, точки лежат на одной окружности, т.е., в самом деле, проходит через

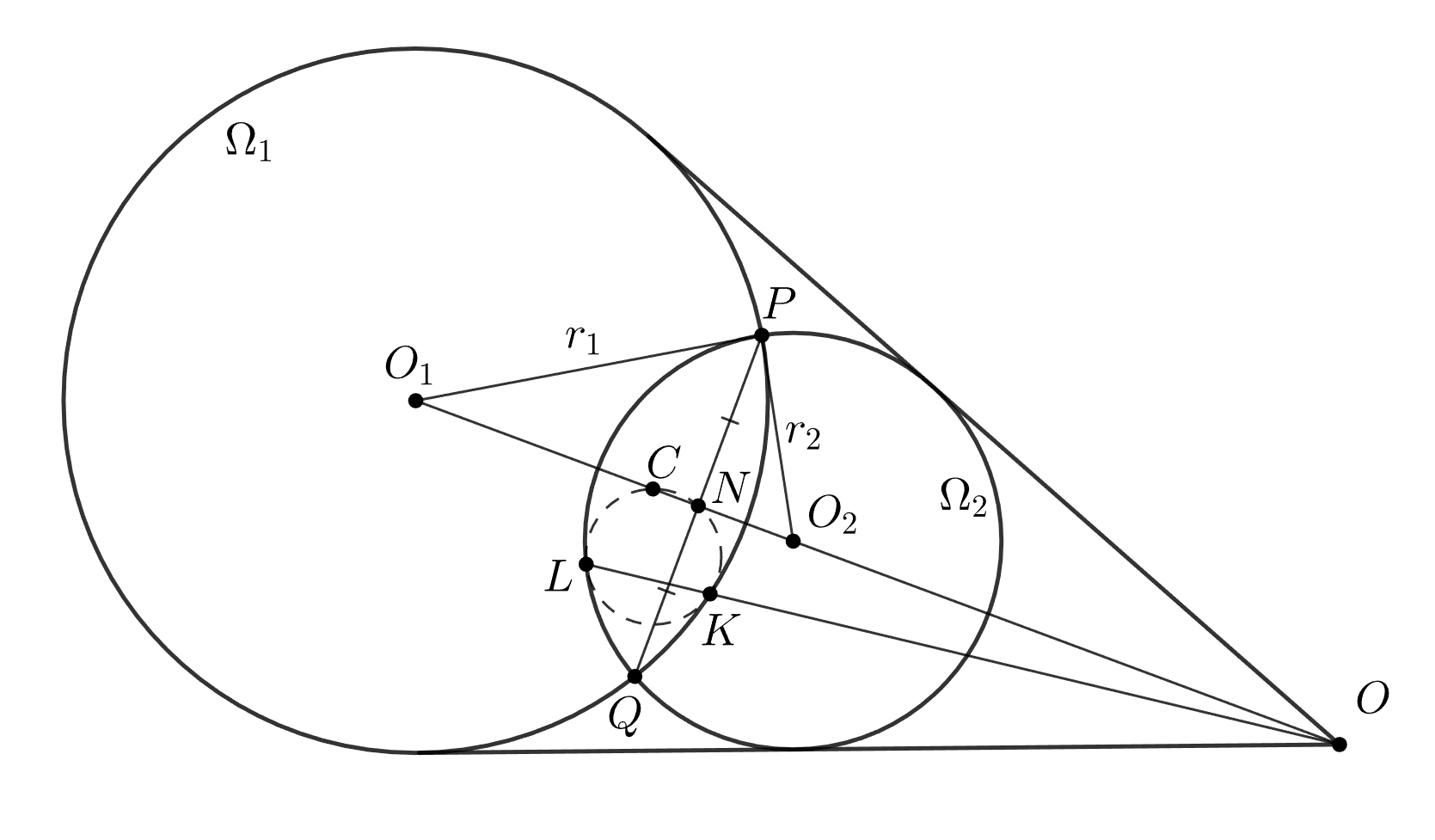
Окружность касающаяся и и лежащая внутри них, с тем условием, что она проходит через , определена единственным образом с точностью до симметрии относительно линии центров.

Пусть общая касательная к и касается их в точках и - середина . Проведем через вторые касательные и к и (пусть и — точки касания). Если мы докажем, что окружность касается и то мы решим задачу, так как эта окружность тогда совпадает с или с симметричным образом относительно

Так как то следовательно, проходит через такую точку на что — диаметр. Касательные, проведенные к и в точках и параллельны, поэтому при гомотетии в с центром в точка переходит в значит, лежит на прямой причем Аналогично, — высота треугольника

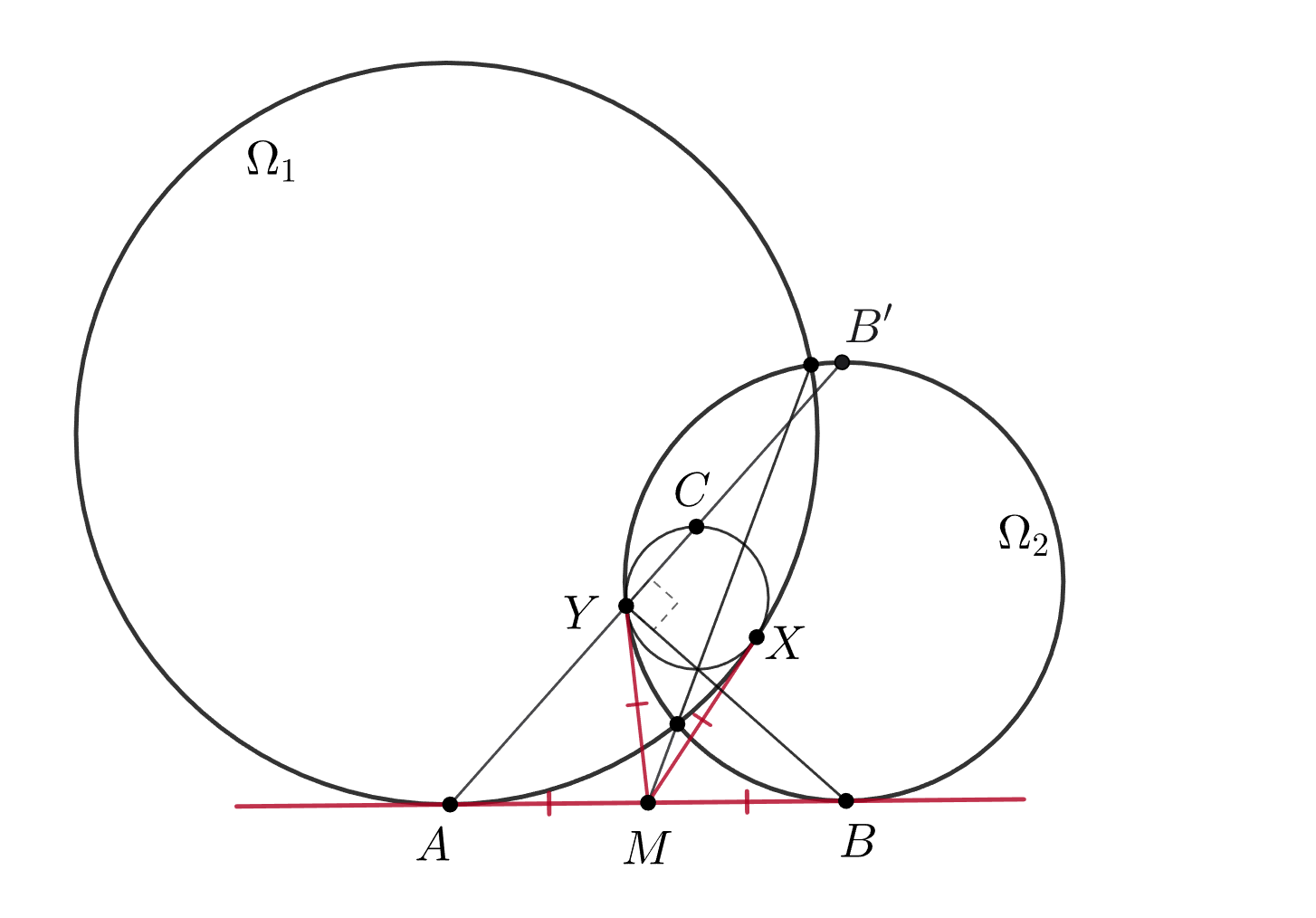
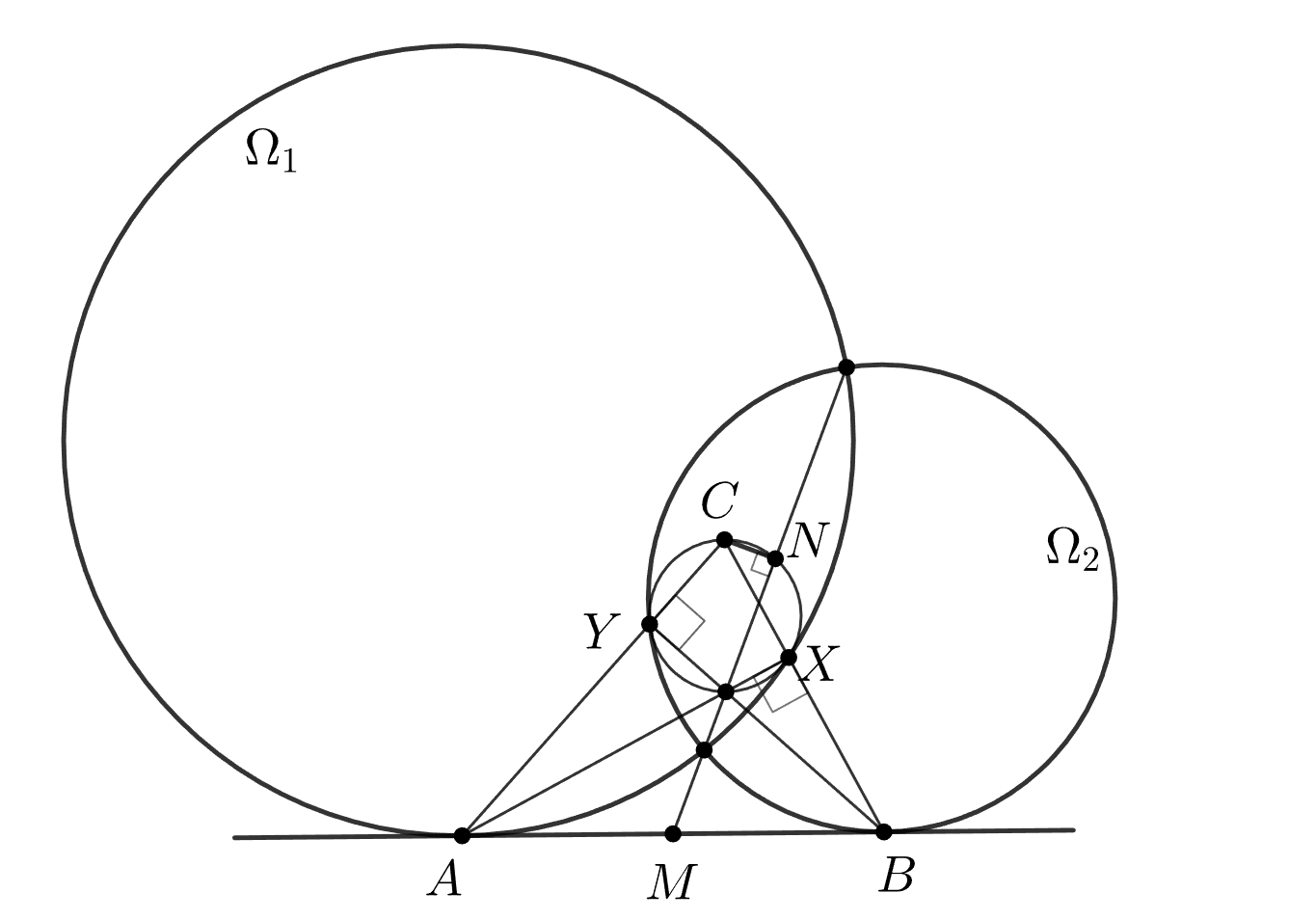
Ортоцентр треугольника имеет равные степени относительно и значит, лежит на Так как точки лежат на окружности с диаметром , т.е. это и есть окружность Так как то окружность касается Аналогично, касается Задача решена.