Степень точки и радикальные оси
Ошибка.
Попробуйте повторить позже
Во вписанном четырёхугольнике проведены биссектрисы углов
,
и
. Они пересекают стороны
четырёхугольника в точках
.
a) Докажите, что точки лежат на одной окружности.
б) Докажите, что точки и
лежат на одной окружности.
Подсказка по пункту (а)
Посчитайте уголки. Посмотрите, как через дуги окружности ABCD выражаются, скажем, углы BXC и YDC.
Подсказка по пункту (б)
Конечно, из пункта (а) также выводится, что точки Z, T, A, B лежат на одной окружности. Теперь подумаем, как применить степень точки. Кажется, на этой картинке пока нет такой точки, степень которой можно посчитать, чтобы доказать вписанность XYZT. Значит, эту точку нужно отметить. При этом хорошо бы использовать другую вписанность, которую мы доказали — то есть CDYX — и, наверное, вписанность ABCD. Пересечение диагоналей XYZT уже выглядит не очень, поэтому попробуйте пересечь стороны AB и CD (вырожденный случай трапеции нужно рассмотреть отдельно) в точке P и посчитать степень точки P относительно разных окружностей.
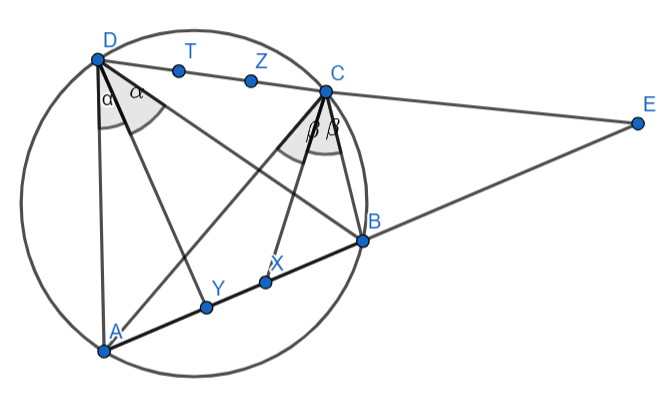
а) Докажем равенство углов и
.
Первый из этих углов , для второго же
.
Поскольку , то равенство выполнено и
.
Заметим, что и
могут располагаться в другом порядке, тогда углы
и
буду опираться на одну дугу и
четырёхугольник также будет вписан.
б) Если стороны и
параллельны, то мы получили вписанную, а значит, равнобокую трапецию (или прямоугольник). В силу
симметрии точки
(в каком-то порядке) будут образовывать равнобокую трапецию (или прямоугольник). Вписанность в этом
случае доказана.
Если , то из первого пункта также следует, что
лежат на одной окружности. Далее будем рассматривать
расположение точек как на картинке, при другом порядке расположения их на сторонах решение аналогично.
Из вписанности ,
и
степень точки
равна:
Из первого и последнего равенства следует вписанность .
а) что и требовалось доказать
б) что и требовалось доказать
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




