Степень точки и радикальные оси
Ошибка.
Попробуйте повторить позже
Из вершины тупого угла треугольника
опущена высота
Проведена окружность с центром
и радиусом
, которая
вторично пересекает стороны
и
в точках
и
соответственно. Найдите
, если
и
Источники:
Подсказка 1
Высота в прямоугольном треугольнике создаст множество различных, удобных для нас подобий, давайте опустим высоты DP и DQ на стороны AB и AC соответственно. Подумайте, какие именно пропорции будут удобны нам для дальнейшего решения.
Подсказка 2
Если вы правильно выбрали пропорции из подобий прямоугольных треугольников на картинке, то заметили, что AP*AB=AD^2 и AQ*AC=AD^2, следовательно, AP*AB=AQ*AC. Подумайте, как от этого выражения перейти к тому, в котором AC будет выражаться через AB, AM, AN (Воспользуйтесь тем, что треугольники ADM и ADN - равнобедренные)
Докажем, что Это можно сделать по-разному.
Первый способ. В прямоугольных треугольниках и
проведём высоты
и
соответственно (см. рис.
10.4a). Тогда
Так как треугольники
и
равнобедренные, то
и
.
Заменив и
в равенстве
, получим требуемое.
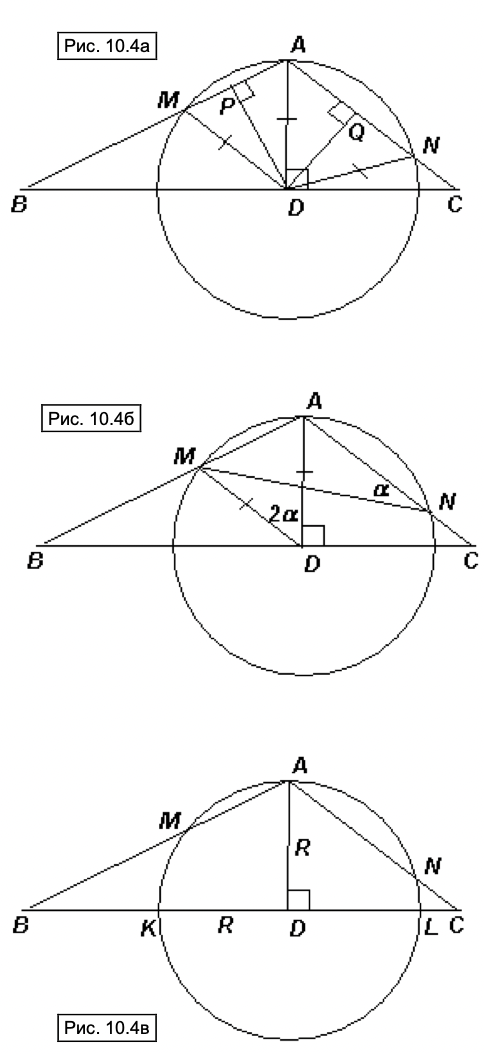
Второй способ. Докажем, что четырёхугольник BMNC вписанный, тогда требуемое равенство будет следовать из теоремы об отрезках
секущих, применённой к точке и окружности, описанной вокруг четырёхугольника BMNC (см. рис. 10.46).
Пусть , тогда
(вписанный и центральный углы, опирающиеся на одну и ту же дугу). Кроме того, из
равнобедренного треугольника
, поэтому
Из равенства
следует, что BMNC -
вписанный.
После того, как доказано указанное равенство, достаточно подставить в него данные из условия задачи и получить ответ.
Третий способ. Пусть данная окружность пересекает отрезки и
в точках
и
соответственно, а ее радиус равен
(см.
рис. 10.4в). Тогда по теореме об отрезках секущих:
, то есть
Из треугольника
по теореме Пифагора:
Следовательно,
, откуда c.
.
Проведя аналогичное рассуждение для стороны , получим, что
Тогда
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




