Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея, Кэзи
Ошибка.
Попробуйте повторить позже
Окружность проходит через вершины
и
треугольника
Окружность
касается
и
в точках
и
соответственно. Пусть
— середина дуги
окружности
Докажите, что прямые
и
пересекаются в одной
точке.
Подсказка 1
Пусть K — точка пересечения пресечения прямых PQ и BC. Как проверить, что данная точка лежит на прямой PM?
Подсказка 2
Показать, что K является основанием биссектрисы внешнего угла, чаще всего это можно доказать, проверив выполнение равенства CK/BK = CT/BT. Как можно иначе выразить последнее отношение?
Подсказка 3
Можно воспользоваться слабой теоремой Кэзи для Ω и точек B, T, C: 0 · BC ± CT · BP ± BT · CQ = 0, откуда CT/BT = CQ/BP. Так, достаточно показать, что CK/BK = CQ/BP, что хорошо, потому что мы избавились от точки T в утверждении. Как доказать последнее утверждение?
Подсказка 4
Достаточно записать теорему Менелая для треугольника ABC и прямой PQ.
Пусть — точка пересечения прямых
и
. Прямая
является биссектрисой внешнего угла
следовательно,
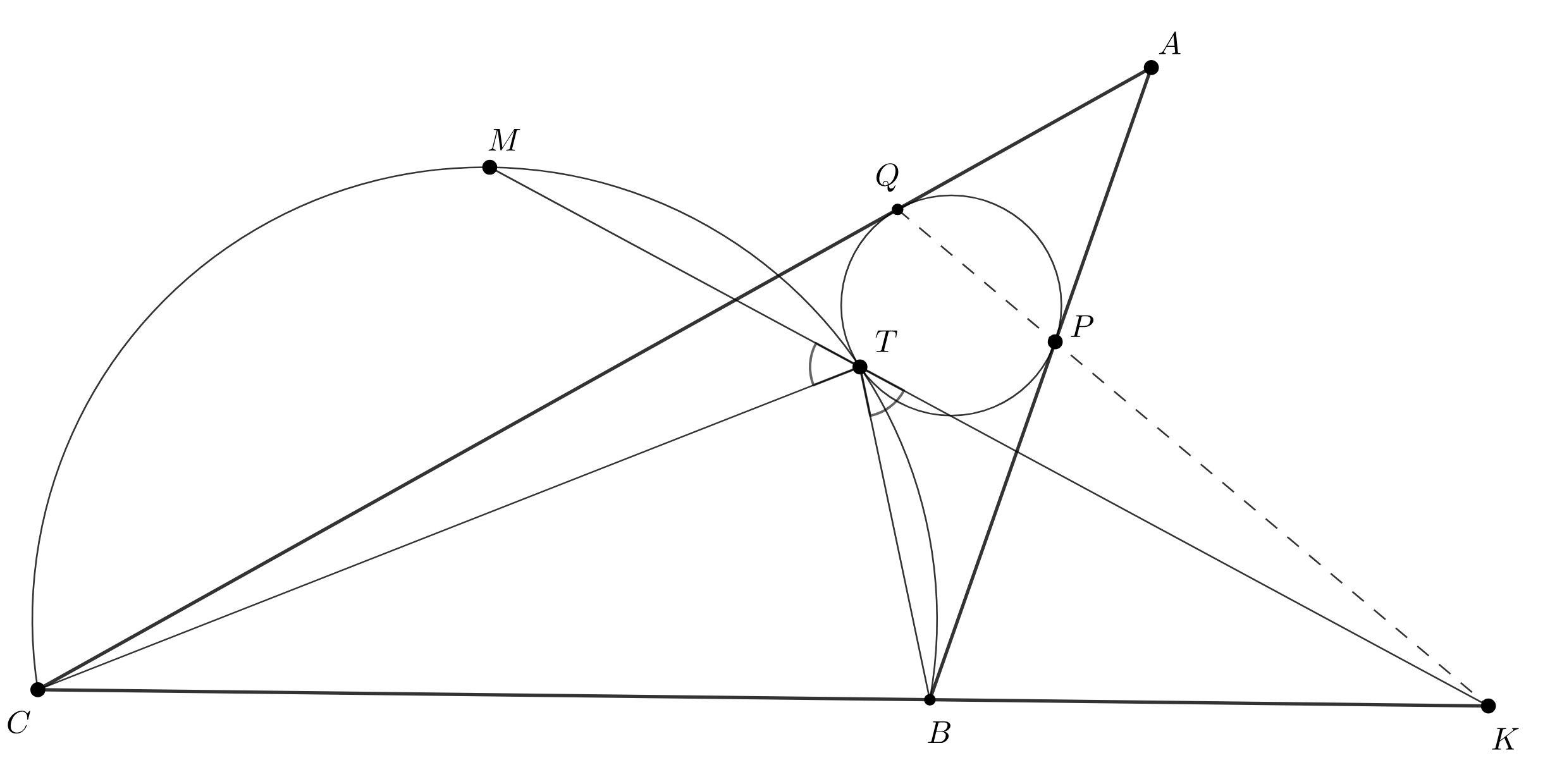
По слабой теореме Кэзи для и точек
имеем
следовательно,
то есть
Наконец, точки лежат на одной прямой, поскольку для них выполнено условие теоремы Менелая
поскольку
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




