Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея

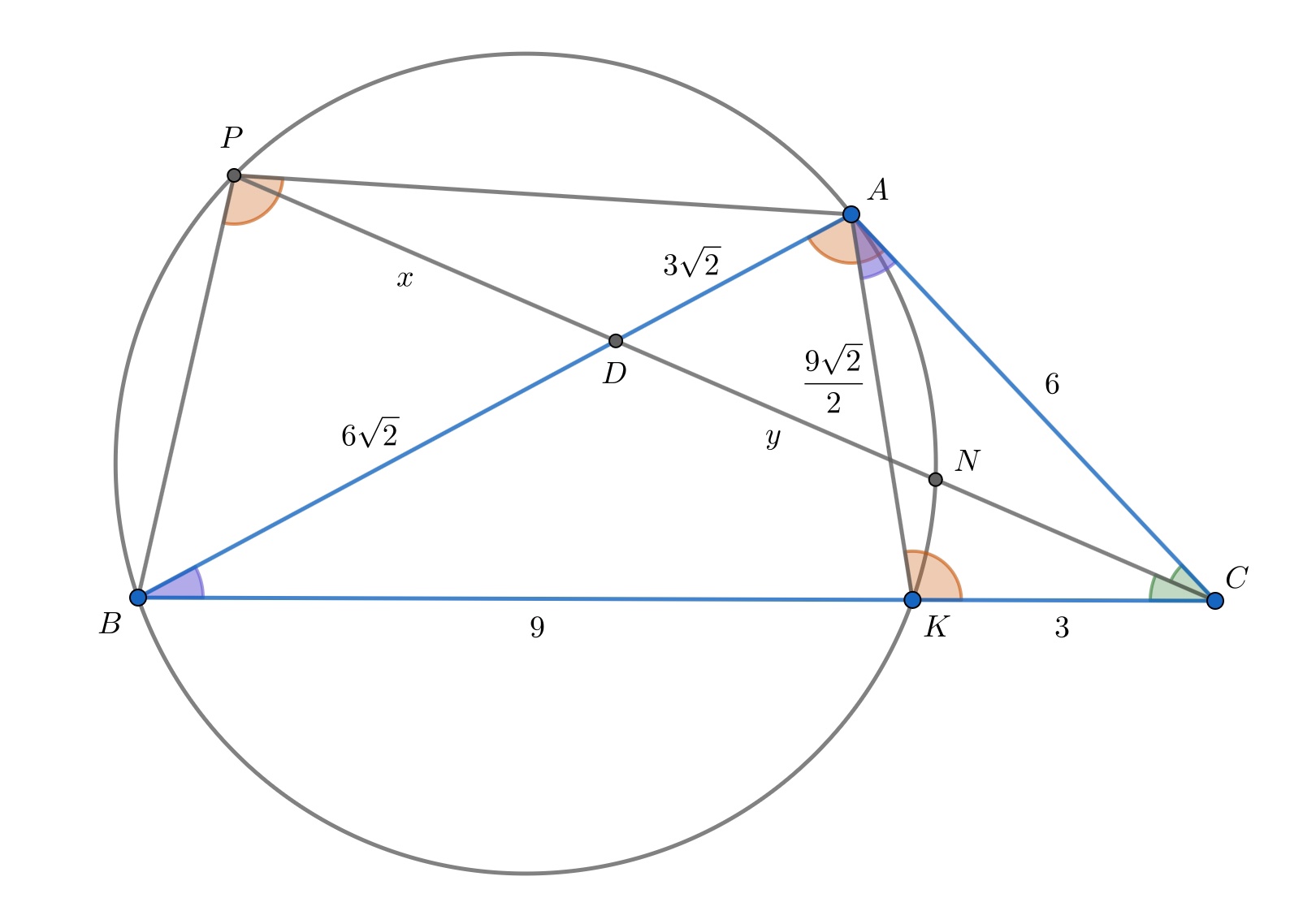
Из условия мы знаем, что а из вписанного четырёхугольника Откуда получаем, следующие равенства

Значит, отрезок является отрезком касательной к окружности. Теперь мы понимаем, что подобен Запишем соответствующие отношения сторон и подставим значения из условия:

Так как мы знаем, что — биссектриса, то запишем свойство, подставив известные значения

К тому же мы нашли поэтому Давайте теперь запишем формулу для биссектрисы и вычислим её:

Пусть где точка пересечения прямой с окружностью, Четырехугольник вписан в окружность, откуда из произведения отрезков хорд

По свойствам касательных и секущих к окружности имеем

Теперь осталось только решить систему из полученных уравнений в пункте

Откуда Решив уравнение, получим