Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея, Кэзи
Ошибка.
Попробуйте повторить позже
Встречайте вновь геометрический вираж...
Определим, конечно же, условия вначале!
Окружность Гамма (очень популярный персонаж),
с
длиной по восемь — хорды дали,
Теперь за точки и
их нарисуем продолжения,
И в точке у получившихся лучей будет пересечение!
Пускай у Гаммы нашей центр где-то в точке
Тогда (просто великолепная прямая)
По линии судьбы (уж так ей суждено)
Отрезочек вдруг в точке
пересекает!
И знаем также, что соотношение дано:
относится к
будто один к четвёрке.
найд̈eте — счастье будет приобретено!
Такая вот задачка для физтех-подборки ;)
(keksenia + ВЕ)
Подсказка 1
Часто ли хорды внутри окружности равны?) Что можно сказать о фигуре, вершинами которой являются концы этих хорд?
Подсказка 2
На картинке есть равнобокая трапеция! А какие равенства она за собой влечёт?
Подсказка 3
Что можно сказать о луче PO?
Подсказка 4
Обратите внимание на то, что PO разделяет два треугольника, у которых можно выделить равные стороны ;)
Подсказка 5
PO — биссектриса угла BPC! А как связать это отношениями, что нам даны?
Подсказка 6
Воспользуемся свойством биссектрисы об отношении отрезков, на которые она делит противоположную сторону!
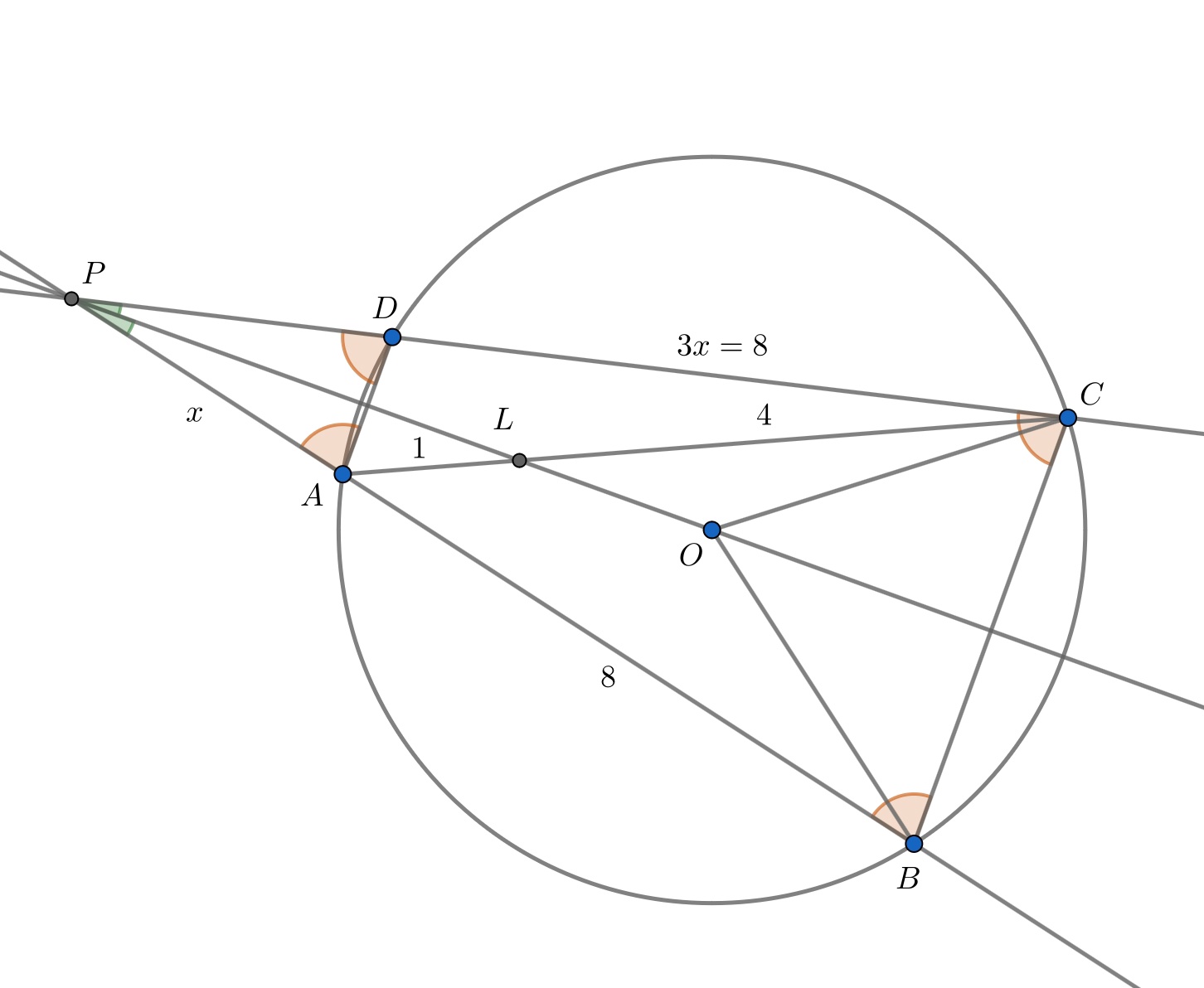
Раз хорды равны и их продолжения пересекаются, то — равнобедренная трапеция и у неё равны углы при основании
поэтому
— равнобедренный треугольник. Следовательно, треугольники
и
равны по трём сторонам, так что
— биссектриса.
По свойству биссектрисы
откуда
и значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




