Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея, Кэзи
Ошибка.
Попробуйте повторить позже
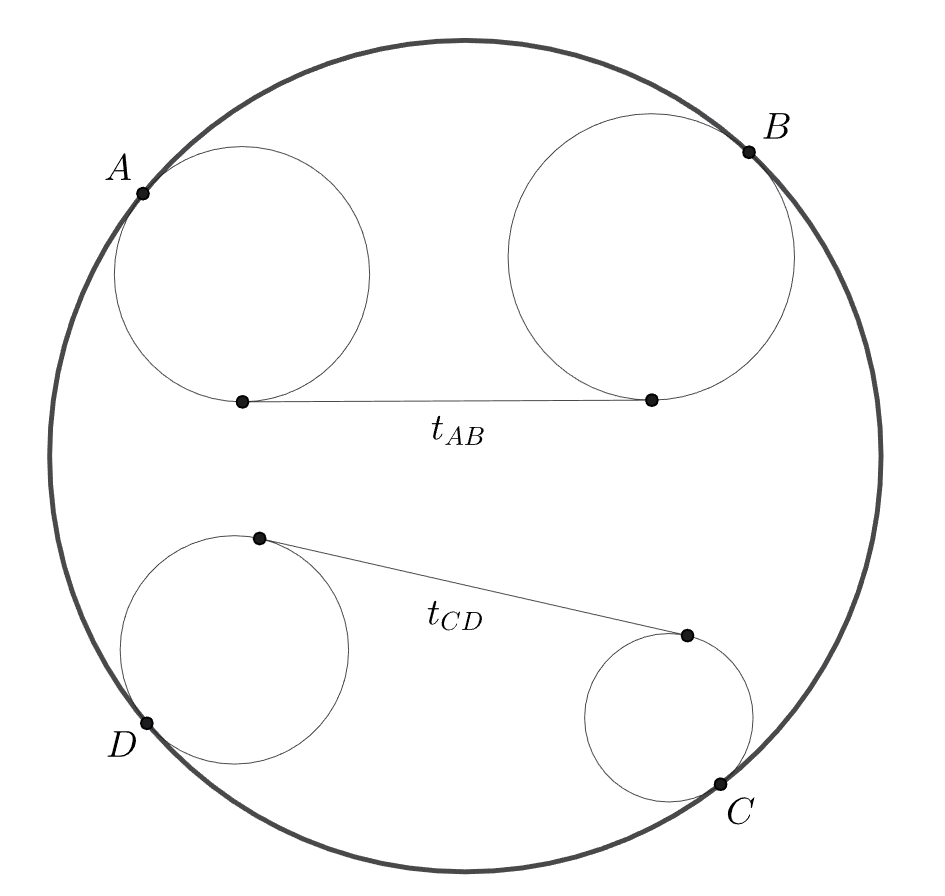
(a) Две окружности и
радиусы которых равны
и
касаются окружности радиуса
в точках
и
Рассмотрим общую
касательную к
и
причем внешнюю, если касания одинаковые и внутреннюю, если разные. Докажите, что длина этой касательной
равна
где знак «
» ставится в случае внешнего касания, а знак «
» — внутреннего. (Можно считать, что
(b) Теорема Кэзи. Дан четырехугольник вписанный в окружность
Рассмотрим окружности
касающиеся
в точках
соответственно. Обозначим через
длину общей касательной к
и
причем
касательная внешняя, если
и
касаются
одинаковым образом и внутренняя, если разным. Аналогичным образом определяются
величины
Докажите, что
a) Будем считать, что оба касания внутренние. Остальные случай касания разбираются аналогично. Докажем следующие утверждение.
Лемма Архимеда. Окружность касается окружности
внутренним образом в точке
а так же хорды
окружности
в
точке
Тогда прямая
проходит через середину дуги
не содержащей точку
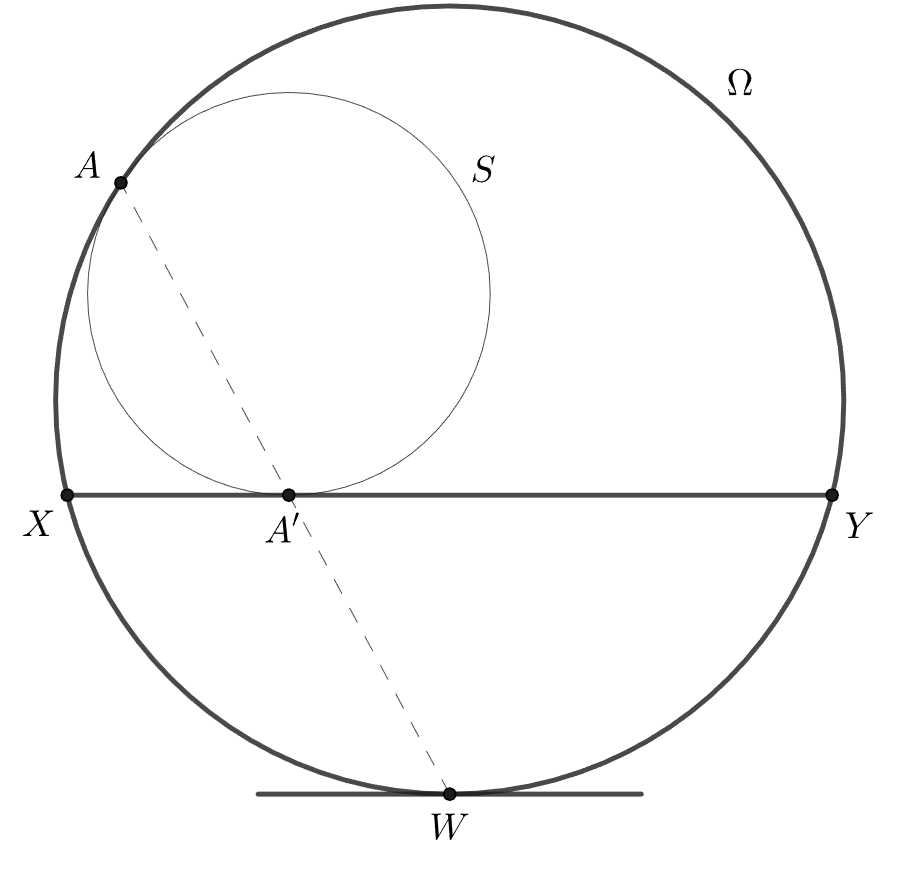
Доказательство. Пусть прямая пересекает
в точке
Рассмотрим гомотетию с центром в точке
переводящую
окружность
в
Пусть прямая
пересекает
в точке
тогда прямая
под действием гомотетии переходит в касательную
к окружности
проведенную в точке
Таким образом, данная касательная параллельна
то есть
является серединой
меньшей дуги
большей окружности.
_________________________________________________________________________________________________________________________________________________________________________________
Вернемся к доказательству задачи. Пусть — большая окружность, общая касательная к окружностям
касается их
соответственно в точках
и
и пересекает
в точках
В силу леммы Архимеда, прямые
и
пересекаются в точке
на окружности
которая является серединой дуги
Докажем, что треугольники и
подобны. Действительно,
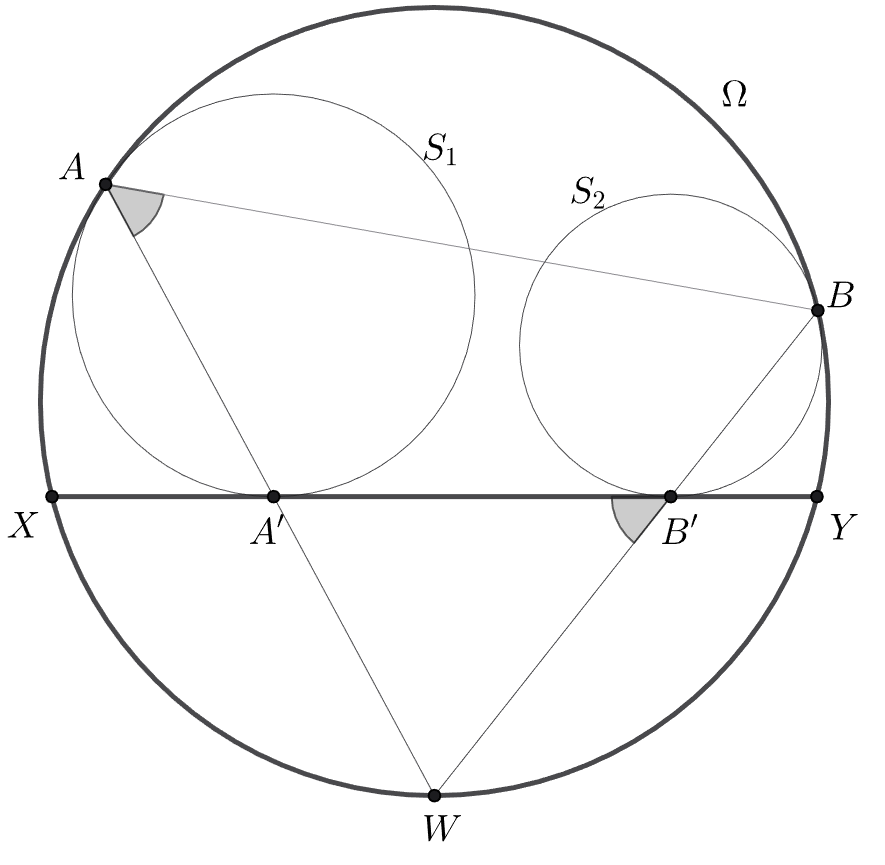
Из подобия
Из доказательства леммы Архимеда, в частности, следует, отношение длин отрезков и
равно отношению радиусов
окружностей
и
следовательно
Подставляя полученные соотношение в правую часть равенства получим требуемое.
b) Будем считать, что все касания внутренние. Пусть радиусы окружностей
соответственно.
В силу пункта (a) имеем
Подставляя в доказываемое равенство данное и аналогичные соотношения и сокращая на последний множитель правой части, получим
что верно в силу теоремы Птолемея для вписанного четырехугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




