Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея, Кэзи

Во-первых, по условию, (как односторонние углы в трапеции), поэтому четырёхугольник — вписанный. Во-вторых, заметим, что точка определена не однозначно: она может оказаться как на продолжении луча за точку так и на отрезке

Первый случай:

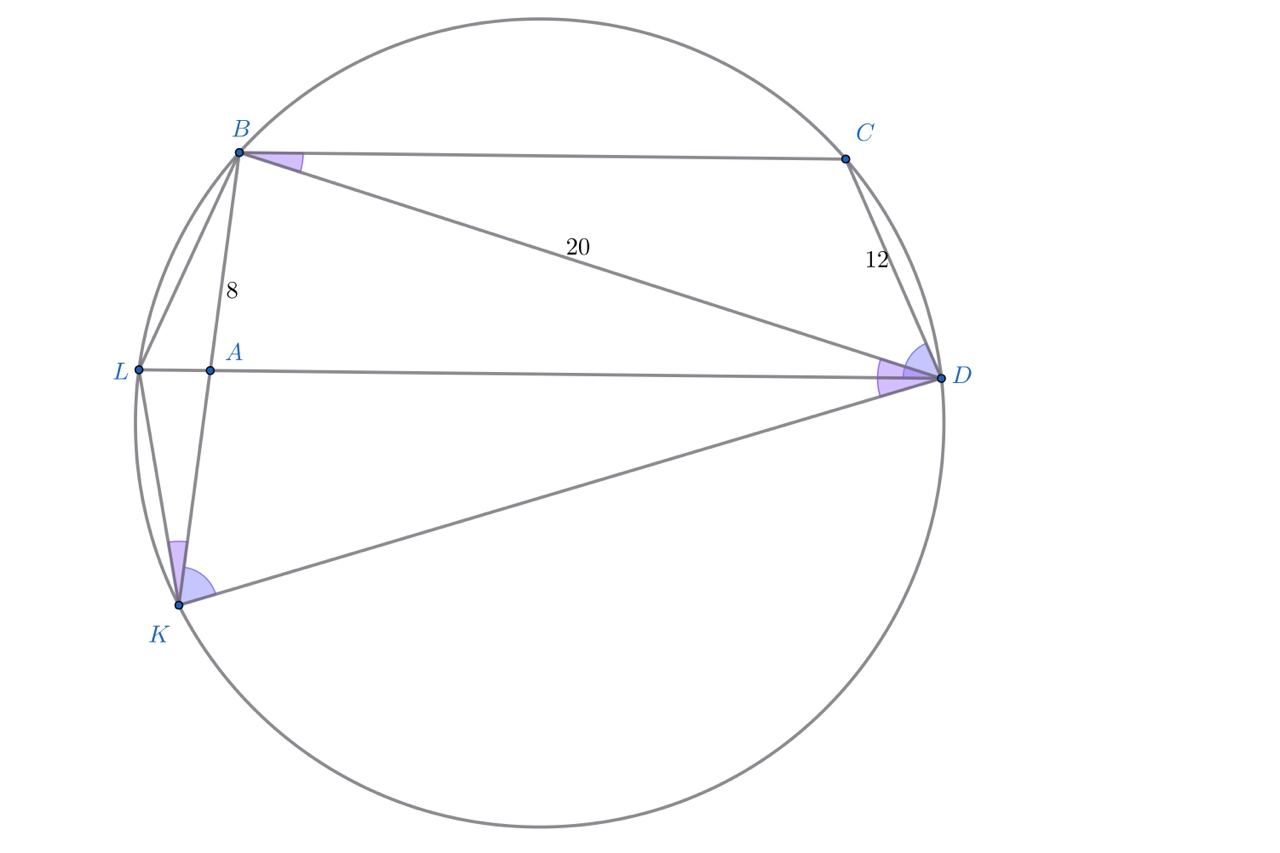
Поймём, что все пять отмеченных на рисунке угла равны: по условию, как накрест лежащий, так как биссектриса. Из равенства получаем, что точка лежит на той же окружности, что и точки и Отсюда как опираюущийся на ту же дуту.

Кроме того, из равенства указанных выше углов также следует, что

Способ Теорема синусов:

Запишем три теоремы синусов. Для треугольника

Для треугольника

Для треугольника

Заметим, что

поэтому наконец, поэтому их синусы также равны.

Значит, произведение правых частей в теоремах синусов равно единице, поэтому

Отсюда

Способ Теорема Птолемея.

По теореме Птолемея для четырёхугольника

Поскольку получаем

По основному свойству биссектрисы для треугольника

Поэтому

Второй случай:

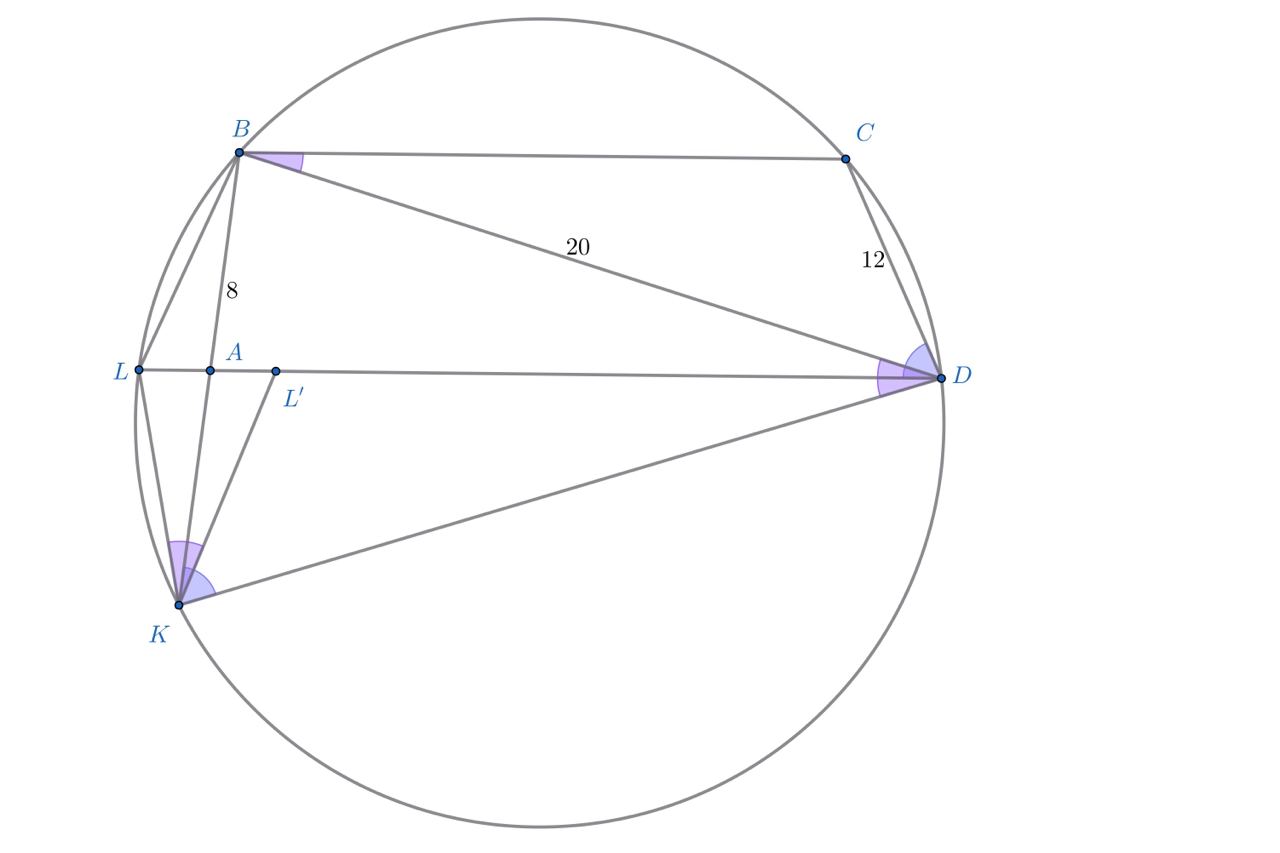
Поскольку мы будем пользоваться свойствами точки из первого случая, лежащую на отрезке «версию» точки назовём Углы и опираются на одну дугу, поэтому равны, то есть вертикальные, поэтому треугольники и подобны,

Значит,

Из того же самого подобия получаем

Теперь заметим, что треугольник подобен треугольнику по двум углам, откуда

Следовательно,