Четырёхугольники в окружности, счёт отрезков и углов, теорема Птолемея, Кэзи
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике длины сторон
и
равны,
— биссектриса угла
Найдите
косинус угла
если
— точка пересечения диагоналей
и
и
Источники:
Подсказка 1
Сразу запишем все отрезки через переменные, пользуясь свойством биссектрисы) Как воспользоваться тем, что у четырехугольника есть две равные стороны? Не забываем, что диагональ DB является биссектрисой!
----—
Подсказка 2
Четырехугольник оказывается вписанным!(почему?). Какое свойство вписанного четырехугольника можно применить, если мы знаем отношения отрезков на его диагонали?
Подсказка 3
Произведение отрезков диагонали равны! Запишем это, и, т.к. у нас все отрезки теперь выражены с помощью двух переменных, сможем применить теорему косинусов, чтобы избавиться от одной переменной) Осталось лишь понять, как искать косинус нужного угла, если мы знаем отношения практически всех отрезков на картинке!
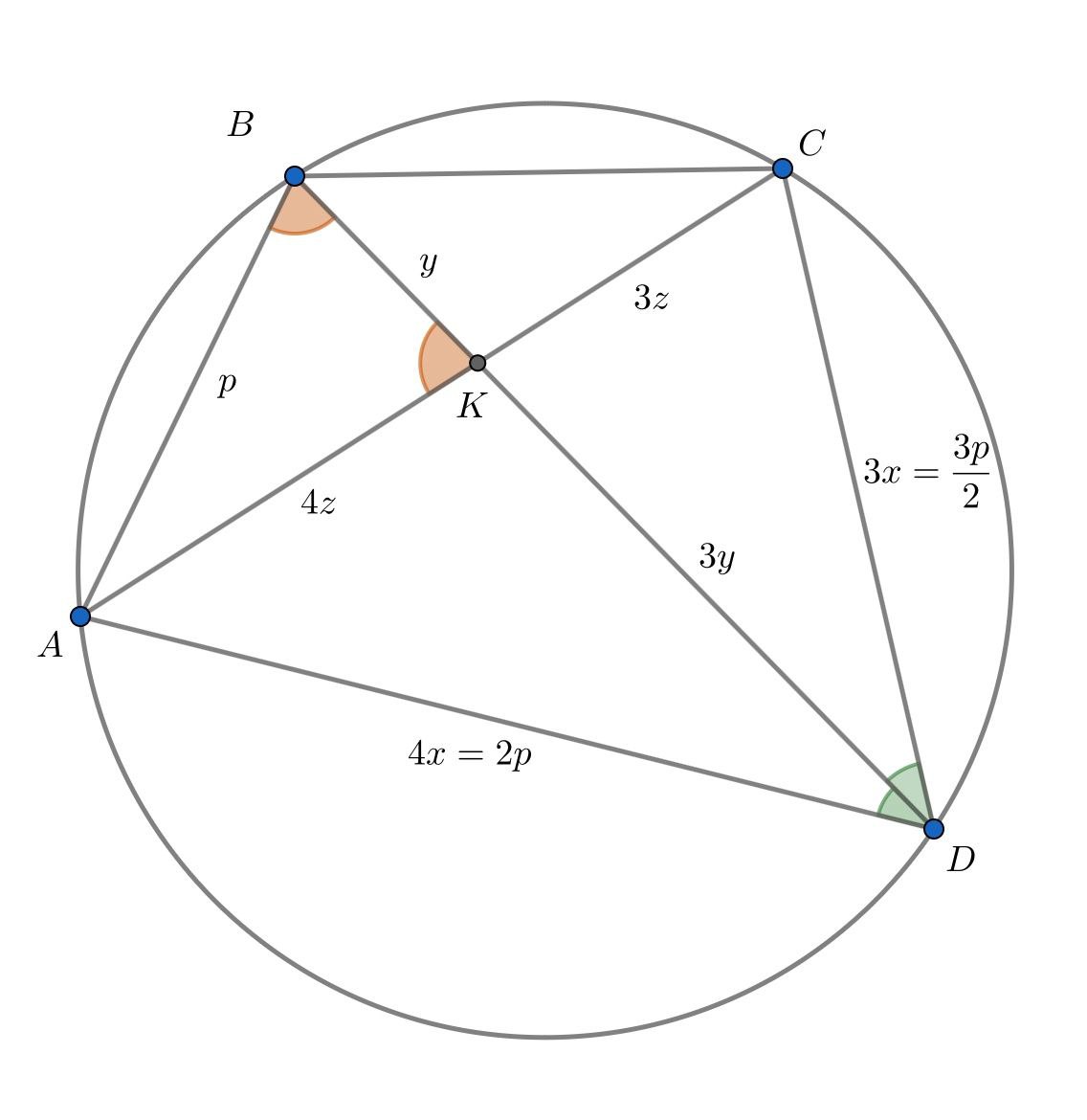
пусть
пусть
— биссектриса треугольника
Точка является точкой пересечения серединного перпендикуляра к диагонали
и биссектрисы угла
в выпуклом
четырехугольнике
Следовательно, около этого четырехугольника можно описать окружность.
Действительно, опишем окружность около треугольника обозначим точку пересечения биссектрисы угла
с окружностью через
Тогда по свойству вписанных углов дуги
и
будут равны, хорды
и
тоже будут равны, треугольник
будет равнобедренным, и серединный перпендикуляр к диагонали
и биссектриса угла
будут пересекаться в точке
Следовательно,
Поскольку около четырехугольника можно описать окружность, то для его диагоналей верно равенство
Треугольник подобен
, и
, пусть
поэтому
По теореме косинусов для треугольников и
с учетом
имеем
Для равнобедренного треугольника имеем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




