Прямоугольные треугольники
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике синус меньшего угла равен . Перпендикулярно гипотенузе проведена прямая, разбивающая треугольник
на две равновеликие части. В каком отношении эта прямая делит гипотенузу?
Подсказка 1
Введём обозначения: пусть нам дан △АВС с гипотенузой АВ и меньшим углом А. Проведённую прямую назовём MN, причём М ∈ АВ, N ∈ AC. Что можно сказать о △ANM и △АВС?
Подсказка 2
Удобно назвать одну из сторон △АВС буквенной переменной и через неё выразить все остальные. Зная отношение площадей подобных треугольников, что можно сказать об их коэффициенте подобия? Исходя из этого найдите АМ относительно введённой переменной. Осталось выразить искомое отношение, и задача решена!
Пусть – точка на гипотенузе
прямоугольного треугольника
,
– точка на катете
и
. Обозначим
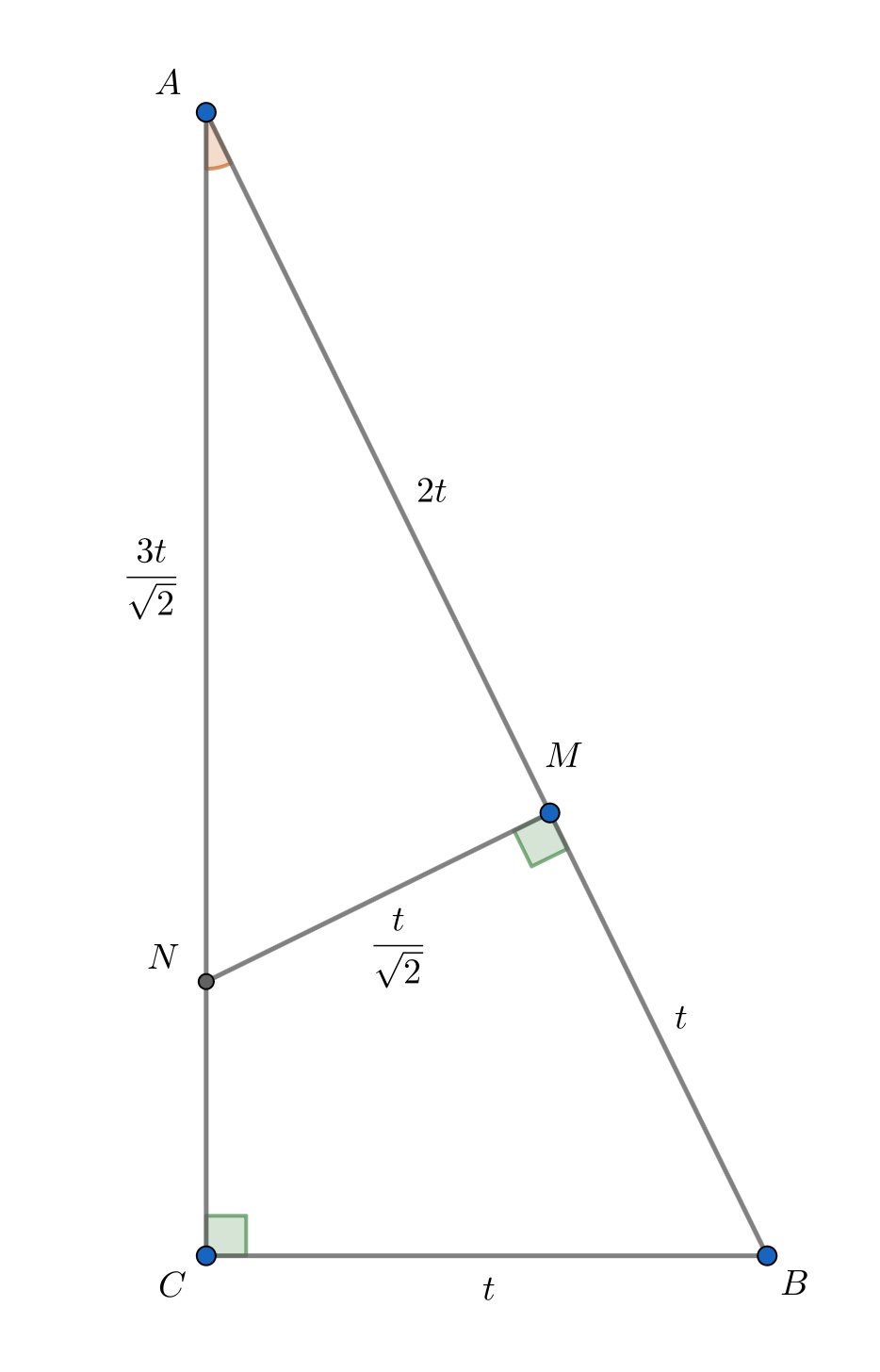
Тогда
Треугольник подобен треугольнику
с коэффициентом, равным квадратному корню из отношения площадей, т. е.
,
значит,
.
Из прямоугольного треугольника находим, что
поэтому
Следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




