Прямоугольные треугольники
Ошибка.
Попробуйте повторить позже
Найдите отрезок, соединяющий середины оснований трапеции, если сумма углов при одном из них равна , а длины оснований равны
и
.
Подсказка 1
Сумма углов при основании трапеции, равная 90°, должна вас сразу наталкивать на мысль продлить боковые стороны до пересечения. Там же получится прямоугольный треугольник!
Подсказка 2
Пусть боковые стороны пересеклись в точке E, а P и R — середины оснований. Если бы эти точки лежали на одной прямой, было бы неплохо!
Подсказка 3
Чтобы доказать это, попробуйте предположить обратное и поотмечать равные углы. Ну и дальше остаётся вспомнить, чему равна медиана, проведённая к гипотенузе)
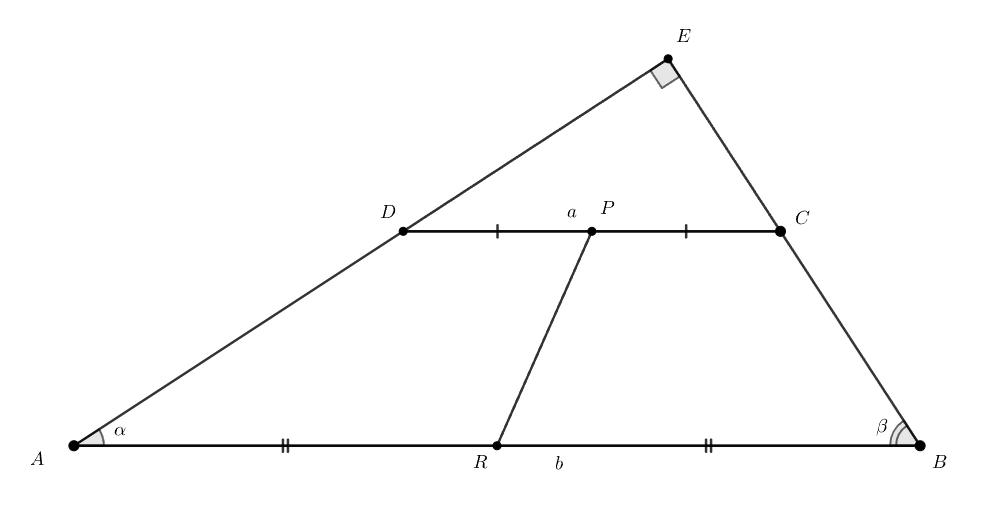
Продлим за точку
,
— за точку
. Эти лучи пересекутся в точке
и образуют прямой угол по условию. Пусть
— середина
,
— середина
. Теперь первое, что хочется доказать, это то, что
лежит на прямой
.
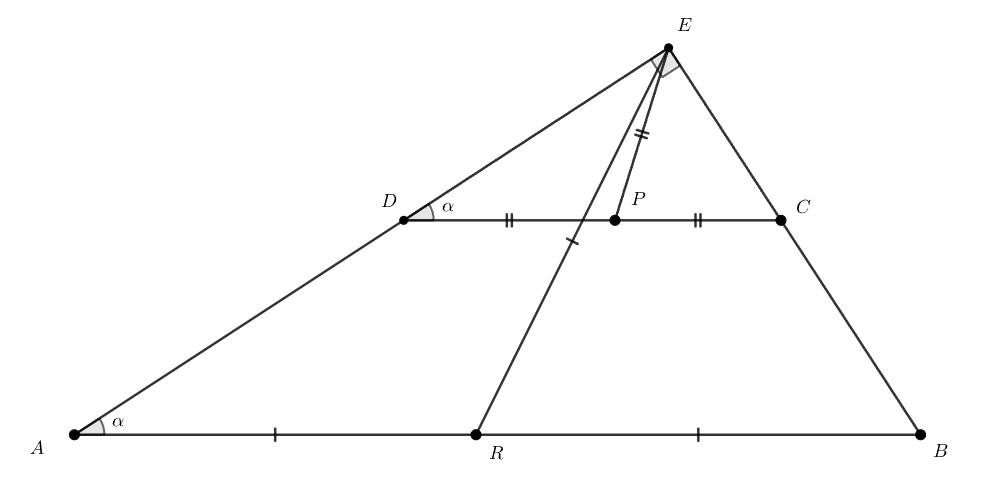
Пусть не так. Тогда проведем и
— медианы прямоугольных треугольников
и
. Поймем, что
как
односторонние углы при параллельных прямых
и
и секущей
. Заметим, что
и
как медианы
прямоугольных треугольников. Значит, треугольники
и
равнобедренные с углом
при основании. И, следовательно,
совпадает с
. Что и требовалось доказать.
Теперь найдем длину отрезка .
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




