Прямоугольные треугольники
Ошибка.
Попробуйте повторить позже
Точки и
— середины сторон
и
параллелограмма
Из его вершины
на прямую
опустили перпендикуляр
На стороне
выбрали точку
так, что углы
и
равны. Найдите
Подсказка 1
Интересно, что нам дает условие про равные углы? На картинке они расположены неудобно. Вот бы придумать доп. построение, чтобы равные углы оказались в одном треугольнике(и тогда он равнобедренный)/равных треугольниках.
Подсказка 2
Давайте продлим KE до пересечения с BC! Тогда возникнет равнобедренный треугольник HFG (где G - точка пересечения BC и EK). А еще возникают равные треугольники EDK и KCG! С этим уже приятнее работать. Подумайте, как теперь применить условие, что BHK - прямой угол (посчитайте уголки на чертеже)
Подсказка 3
Можно доказать, что BHF тоже равнобедренный! Какая приятная картинка - так много равных сторон. Давайте обозначать их за переменные. Например, ED = a, FC = b (или как-то по-другому на ваше усмотрение). Осталось выразить BF:FC, используя факты из прошлых подсказок
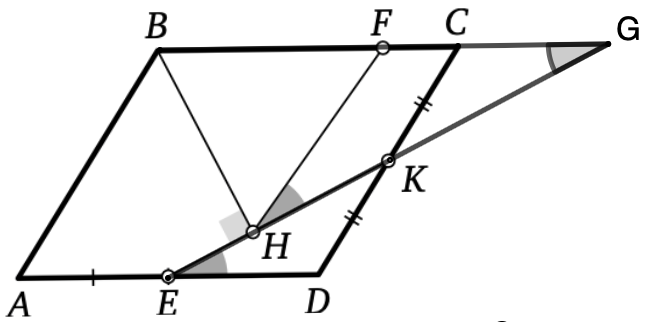
Продлим за точку
пересечем с прямой
получим точку
как накрест лежащие при параллельных
прямых
и
и секущей
а значит, треугольник
равнобедренный и
Аналогично треугольник
равнобедренный с углом при основании
то есть
Отсюда
Рассмотрим
треугольники
и
Они равны по стороне и двум прилежащим к ней углам
как
накрест лежащие углы при параллельных прямых). Значит,
пусть
тогда
отсюда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




