Треугольник с углом 60 градусов
Ошибка.
Попробуйте повторить позже
На плоскости задана точка . Рассматриваются различные равносторонние треугольники
, такие что
Какое
максимальное значение может принимать длина отрезка
Источники:
Счётный способ, подсказка 1
Заметим, что если зафиксировать треугольник PAB, то картинка определяется единственным образом. Как его зафиксировать?
Счётный способ, подсказка 2
Конечно, можно ввести лишь три его стороны, но лучше ввести еще и два угла, чтобы счет проходил легче(а с помощью теорем синусов или косинусов, мы всегда сможем связать углы со сторонами при желании).
Счётный способ, подсказка 3
Выразите сторону AB по теореме косинусов и угол PBA через стороны треугольника PAB и угол APB. Выразили? Кажется, все готово, чтобы считать PC.
Счётный способ, подсказка 4
Попробуйте привести выражение PC к такому виду, чтобы только одно слагаемое было переменным, а все остальное являлось константой.
Геометрический способ, подсказка 1
На картинке есть угол 60 градусов и два равных отрезка исходящих из него(AB и AC). Это очень сильно намекает на поворот в этой точке.
Геометрический способ, подсказка 2
Да, нужно сделать поворот на 60 градусов, переводящий точку B в точку C. Это удобно, так как точка P переедет в точку P’,при этом APP’-равносторонний и треугольники AP’C и APB равны. Какой вывод о длине PC можно сделать?
Геометрический способ, подсказка 3
Да, по неравенству треугольника PC<=5. Осталось лишь привести пример, но как? Попробуйте делать те же действия, как вы получили оценку, но в обратном порядке, не забывая о том, когда эта оценка достигается(расположение точек P,P’,C)
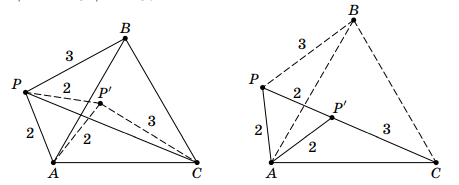
Первое решение.
Докажем, что длина не больше . Для этого рассмотрим поворот с центром в точке
на
таким образом, что
переходит в
.
Точка
переходит в
, а поскольку
и
, то
, откуда
по
неравенству треугольника.
Для построения примера сначала построим правильный , затем на продолжении
отметим
. Наконец, построим
правильный треугольник
на отрезке
. Остаётся показать, что выполнено
, но для этого достаточно рассмотреть поворот
на
в обратную сторону
, тогда отрезок
перейдёт в
.
Второе решение.
Просто посчитаем. Пусть ,
. Тогда из треугольника
из теоремы косинусов
следует
Теперь из треугольника по теореме косинусов
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




